18 Análise de variância
18.1 Introdução
Os conteúdos desta seção e da seção seguinte (seção 18.2) podem ser visualizados neste vídeo.
Amess et al. (Amess et al. 1978) realizaram um estudo prospectivo, onde avaliaram os níveis de ácido fólico (microgramas por litro) nas células vermelhas em pacientes com bypass cardíaco que receberam três métodos diferentes de ventilação durante a anestesia.
Os dados desse estudo estão disponíveis no conjunto de dados red.cell.folate do pacote ISwR (GPL-2 | GPL-3) (figura 18.1).

Figura 18.1: Descrição das variáveis que compõem o conjunto de dados red.cell.follate.
Os três métodos de ventilação são:
- N2O-O2, 24h: 50% óxido nitroso e 50% oxigênio continuamente por 24 horas;
- N2O-O2, op: 50% óxido nitroso e 50% oxigênio somente durante a operação;
- O2, op: 35-50% oxigênio continuamente por 24 horas.
O conteúdo do conjunto de dados red.cell.folate é mostrado a seguir:
library(RcmdrMisc)
library(ISwR)
data(red.cell.folate, package="ISwR")
red.cell.folate## folate ventilation
## 1 243 N2O+O2,24h
## 2 251 N2O+O2,24h
## 3 275 N2O+O2,24h
## 4 291 N2O+O2,24h
## 5 347 N2O+O2,24h
## 6 354 N2O+O2,24h
## 7 380 N2O+O2,24h
## 8 392 N2O+O2,24h
## 9 206 N2O+O2,op
## 10 210 N2O+O2,op
## 11 226 N2O+O2,op
## 12 249 N2O+O2,op
## 13 255 N2O+O2,op
## 14 273 N2O+O2,op
## 15 285 N2O+O2,op
## 16 295 N2O+O2,op
## 17 309 N2O+O2,op
## 18 241 O2,24h
## 19 258 O2,24h
## 20 270 O2,24h
## 21 293 O2,24h
## 22 328 O2,24hAs medidas de tendência central e dispersão da variável folate para cada método de ventilação são apresentadas a seguir e a figura 18.2 mostra o correspondente diagrama de pontos.
numSummary(red.cell.folate[,"folate", drop=FALSE],
groups=red.cell.folate$ventilation,
statistics=c("mean", "sd", "IQR", "quantiles"),
quantiles=c(0,.25,.5,.75,1))## mean sd IQR 0% 25% 50% 75% 100% folate:n
## N2O+O2,24h 316.6250 58.71709 91.5 243 269 319 360.5 392 8
## N2O+O2,op 256.4444 37.12180 59.0 206 226 255 285.0 309 9
## O2,24h 278.0000 33.75648 35.0 241 258 270 293.0 328 5with(red.cell.folate, Dotplot(folate, by=ventilation, bin=FALSE))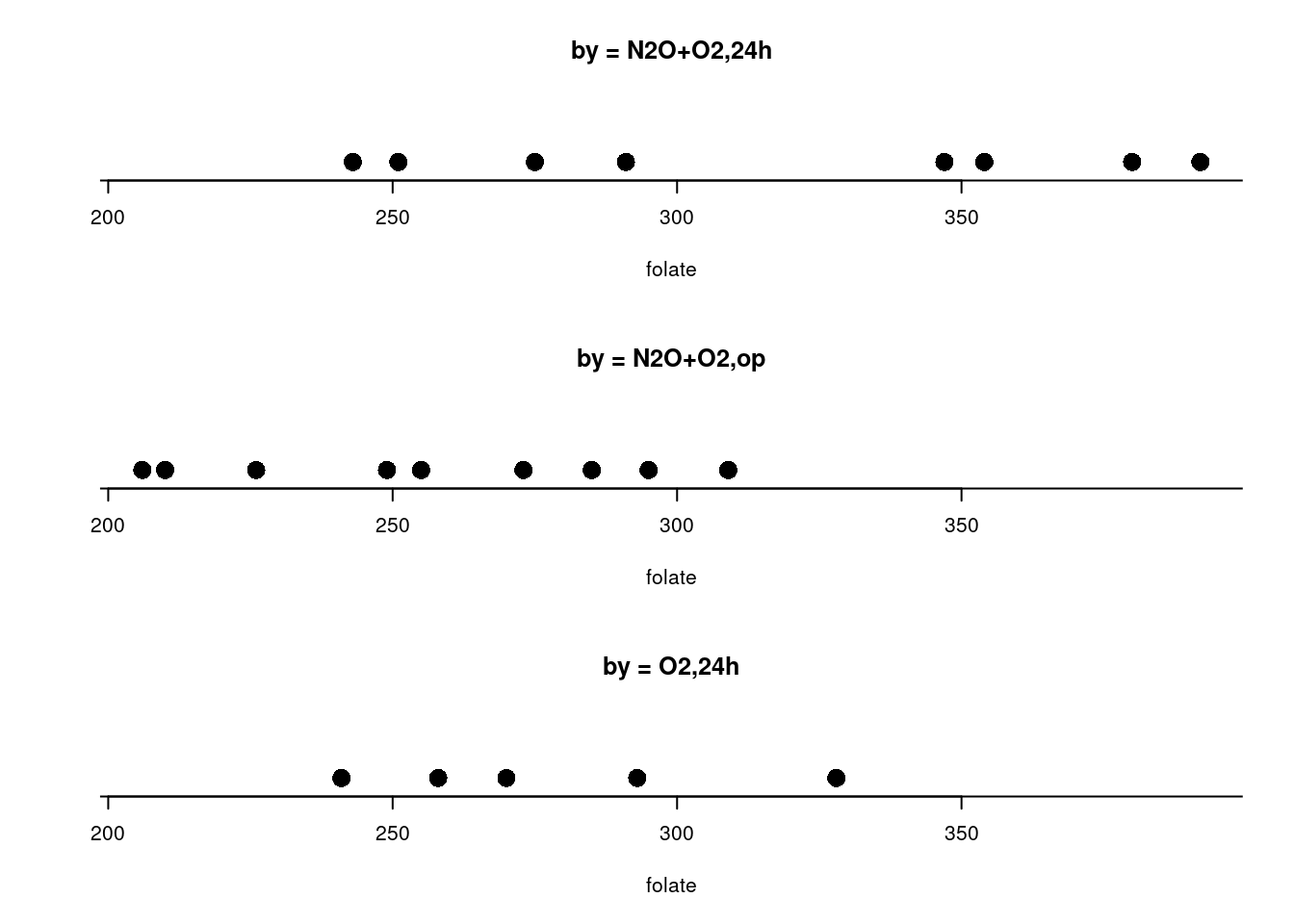
Figura 18.2: Diagrama de pontos da variável ácido fólico para cada método de ventilação.
O capítulo 16 explorou técnicas estatísticas para verificar se uma variável numérica possui a mesma distribuição em duas populações independentes ou não, assim como a determinação do intervalo de confiança para a diferença de médias entre as duas populações.
Generalizando o problema, poderíamos estar interessados em saber se a variável folate estaria distribuída da mesma forma em cada método de ventilação ou quais seriam as diferenças de médias de ácido fólico entre os diversos métodos de ventilação. Neste capítulo, será introduzida a técnica estatística conhecida como Análise de Variância (ANOVA), utilizada para a comparação das médias de uma variável aleatória numérica em mais de duas populações.
A variável numérica cujas médias estão sendo comparadas em três ou mais populações é chamada de variável resposta ou dependente. A variável categórica que distingue as diversas populações em estudo é chamada de variável de tratamento, ou fator, ou variável explanatória, ou variável independente. As perguntas que devem ser respondidas são:
- Os diferentes níveis do fator em estudo resultam em diferenças de médias na variável resposta?
- Se sim, como quantificar essas diferenças?
Esse é o tipo mais simples de análise de variância e é conhecida como análise de variância com um fator, onde uma única fonte de variação é avaliada em mais de duas amostras independentes, sendo uma extensão do teste t para duas amostras independentes.
A análise de variância com um fator é utilizada para testar a hipótese nula de que as distribuições da variável resposta em cada nível do fator em estudo é a mesma e também para obter intervalos de confiança para contrastes entre as médias da variável resposta nos diversos níveis do fator. No exemplo considerado no início deste capítulo, a ANOVA pode ser utilizada para verificar se as médias do ácido fólico são as mesmas em cada método de ventilação e, eventualmente, estabelecer intervalos de confiança para diferenças das médias de ácido fólico entre os diversos métodos.
18.2 Múltiplas comparações
Uma primeira ideia para comparar as médias de ácido fólico entre os três métodos de ventilação no conjunto de dados red.cell.folate seria realizar um teste t com um nível \(\alpha\) de significância para cada par de métodos de ventilação e considerar estatisticamente significativas aquelas comparações cujo valor de p fosse menor que \(\alpha\). Como temos 3 métodos de ventilação, esse raciocínio é equivalente a realizar 3 testes estatísticos, comparando dois a dois todos os pares de métodos. Em cada teste, a probabilidade de não rejeitar a hipótese nula quando ela é verdadeira é \(1 - \alpha\).
Supondo que os 3 testes sejam independentes e que a hipótese nula seja verdadeira em todos eles, a probabilidade de todos os testes não serem estatisticamente significativos é de \((1 - \alpha)^3\). Logo a probabilidade de pelo menos um deles ser estatisticamente significativo é de \(1-(1 - \alpha)^3\). Se tomarmos \(\alpha\) = 5%, por exemplo, o erro tipo I para o conjunto de testes não será 5%, mas 1 - (1 - 0,05)3 = 0,14 (14%).
Esse é o problema quando múltiplos testes são realizados, especialmente quando são realizados de maneira exploratória, sem terem sido previamente planejados. Nesse exemplo, o mais adequado é realizar um único teste para verificar se existe alguma diferença entre os métodos de ventilação tomados em conjunto. Caso o teste indique que as médias sejam diferentes, então uma análise mais detalhada seria realizada para determinar onde estão estas diferenças e calcular os intervalos de confiança de tal forma que, em conjunto, tenham o nível de confiança desejado. Esses são os objetivos da Análise de Variância.
18.3 Análise de variância com um fator
18.3.1 Modelo de efeitos fixos
Os conteúdos desta seção e da seção 18.3.2 podem ser visualizados neste vídeo.
Na análise de variância com um fator, amostras são extraídas das populações correspondentes a cada nível do fator em estudo. A rigor, essas amostras deveriam ser aleatórias para justificar a aplicação das técnicas estatísticas descritas a seguir. Entretanto, em muitos estudos, essas amostras são obtidas por conveniência, na suposição de que de que não haja viéses na seleção dos pacientes.
Vamos supor que temos k níveis do fator e que ni representa o tamanho da amostra correspondente ao nível i, i variando de 1 a k. O modelo para a análise de variância com um fator pode ser escrito como:
\[\begin{align} X_{ij} = \mu_{i} + \epsilon_{ij} = \mu + \alpha_{i} + \epsilon_{ij} \tag{18.1} \end{align}\]
onde:
i - indica cada nível do fator em estudo (i = 1, 2, …, k).
j - indica cada uma das observações da variável resposta em cada amostra (j = 1, 2, …, \(n_{i}\)).
\(X_{ij}\) - valor da variável resposta correspondente à observação j da amostra i.
\(\mu_{i}\) - média da variável X na população correspondente ao nível i do fator de estudo. Representa o efeito do nível i do fator em estudo.
\(\epsilon_{ij}\) - erro associado à observação j da amostra i, diferença entre o valor de \(X_{ij}\) e a média da população i.
\(\mu\) - média geral da variável X em todas as populações no estudo.
\(\alpha_{i}\) - diferença entre a média da variável X na população correspondente ao nível i do fator de estudo e a média geral, \(\alpha_i = \mu_{i} - \mu\).
Ao olharmos para esse modelo, podemos ver que uma observação típica do conjunto total de dados em estudo é composta de: 1) média geral de todos os tratamentos (\(\mu\)); 2) um efeito diferencial de cada tratamento (\(\alpha_{i}\)); e 3) um termo de erro (\(\epsilon_{ij}\)), representando o desvio da observação em relação à média de seu grupo.
Esse modelo é chamado de modelo de efeitos fixos, porque estamos interessados somente nesses níveis do fator em estudo. No caso da relação entre os métodos de ventilação e os níveis de ácido fólico, esse modelo supõe que os autores não estão interessados em nenhum outro método de ventilação além dos três utilizados. Em outros tipos de estudos, os níveis do fator estudado poderiam ser um subconjunto de todos os níveis possíveis. Nesses casos, o modelo seria chamado de modelo de efeitos aleatórios.
As suposições do modelo de efeitos fixos são as seguintes:
• as k amostras são amostras independentes das respectivas populações;
• cada uma das populações de onde as amostras foram extraídas é normalmente distribuída com média \(\mu_{i}\) e variância \(\sigma^2\);
• as populações possuem a mesma variância, isto é, \(\sigma_1^2 = \sigma_2^2 =\dots =\sigma_k^2 =\sigma^2\);
• as médias \(\mu_{i}\) são constantes desconhecidas e \(\sum_{i=1}^{k}\alpha_{i}=0\), uma vez que a soma dos desvios de \(\mu_{i}\) em relação à média geral é 0;
• os \(\epsilon_{ij}\) são normalmente e independentemente distribuídos com mesma variância, ou seja, \(\epsilon_{ij} \sim N(0, \sigma^2)\).
18.3.2 Teste de hipótese
Na análise de variância de modelos de efeitos fixos com um fator, a hipótese nula para um teste bilateral é que as médias das populações correspondentes a cada nível do fator são iguais e a hipótese alternativa é que pelo menos uma das médias é diferente das demais:
H0: \(\mu_{1} = \mu_{2} = \dots = \mu_{k}\)
H1: nem todas as médias \(\mu_{i}\) são iguais
Se as médias das populações são iguais, então o efeito diferencial de cada nível do fator é igual a 0. Então a hipótese nula e a alternativa poderiam ser escritas como:
H0: \(\alpha_{i} = 0,\ \ \ \ \ i = 1, 2, ..., k\)
H1: nem todos os \(\alpha_{i} = 0\)
Se H0 for verdadeira e as suposições de igualdade de variâncias e distribuição normal das populações forem satisfeitas, as funções densidade de probabilidade das populações se parecerão com a figura 18.3. Nesse caso, as médias e as variâncias das populações são todas iguais e as respectivas distribuições de probabilidades serão superpostas.
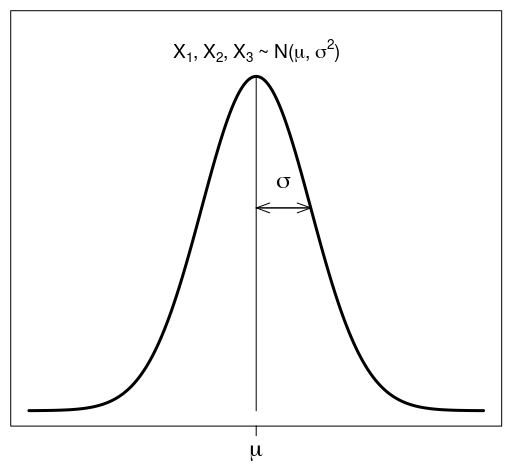
Figura 18.3: Situação em que as médias das populações correspondentes a cada nível do fator em estudo são iguais.
Quando H0 for falsa, ela pode ser falsa, porque uma das populações possui a média diferente das demais, que são iguais, ou todas as populações possuem médias diferentes; há diversas outras possibilidades. A figura 18.4 mostra a situação em que as suposições são satisfeitas, mas H0 é falsa, porque todas as médias são diferentes, considerando que um fator com três níveis esteja sendo estudado.
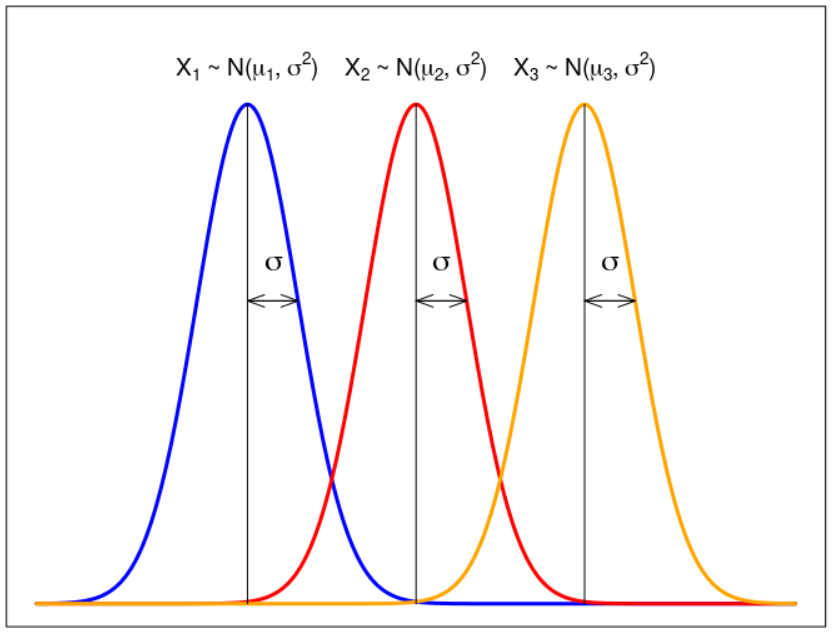
Figura 18.4: Situação em que as médias das populações correspondentes a cada nível do fator em estudo são diferentes para um fator com três níveis.
Para verificar a hipótese H0, vamos considerar a situação em que uma variável aleatória X foi medida em k populações diferentes, definida por k níveis de uma variável categórica (fator). Para cada nível do fator, uma amostra aleatória com ni elementos foi extraída. O número total de valores medidos da variável X, nT é igual a:
\[\begin{align} n_T = \sum_{i=1}^{k} n_i \tag{18.2} \end{align}\]
A média aritmética de todos os valores de X (média geral) é dada por:
\[\begin{align} \bar{X} = \frac{\sum_{i=1}^{k} \sum_{j=1}^{n_i} X_{ij}} {n_T} \tag{18.3} \end{align}\]
A média aritmética dos valores de X para cada grupo é dada por:
\[\begin{align} \bar{X_i} = \frac{\sum_{j=1}^{n_i} X_{ij}} {n_i} \tag{18.4} \end{align}\]
onde i = 1, 2, …, k.
Partição da soma dos resíduos em relação à média geral
A expressão a seguir mostra que o desvio de cada valor da variável aleatória em relação à média geral é igual ao desvio em relação à média do respectivo grupo somado ao desvio da média do respectivo grupo em relação à média geral:
\(\begin{aligned} \underbrace{X_{ij} - \bar{X}}_\text{desvio em relação à média geral} = \underbrace{(X_{ij} - \bar{X_i})}_\text{ desvio em relação à média do grupo} + \underbrace{(\bar{X_i} - \bar{X})}_\text{desvio da média do grupo em relação à média geral} \end{aligned}\)
Elevando cada desvio ao quadrado e somando os quadrados de todos os desvios, pode-se mostrar que o resultado é a expressão abaixo:
\(\sum_{i=1}^{k}\sum_{j=1}^{n_i}(X_{ij} - \bar{X})^2 = \sum_{i=1}^{k}\sum_{j=1}^{n_i}(X_{ij} - \bar{X_i})^2 + \sum_{i=1}^{k}\sum_{j=1}^{n_{i}}(\bar{X_i} - \bar{X})^2\)
Essa expressão pode ser escrita como:
\(SQTot = SQE + SQEG\)
onde:
\(\text{SQTot = Soma total dos quadrados} = \sum_{i=1}^{k}\sum_{j=1}^{n_{i}}(X_{ij} - \bar{X})^2\)
\(\text{SQE = Soma dos quadrados dos desvios dentro de cada grupo =} \sum_{i=1}^{k}\sum_{j=1}^{n_{i}}(X_{ij} - \bar{X_i})^2\)
\(SQEG =\text{ Soma dos quadrados dos desvios dos grupos em relação à média}\)
\(= \sum_{i=1}^{k}\sum_{j=1}^{n_{i}}(\bar{X_i} - \bar{X})^2\)
\(= \sum_{i=1}^{k}n_{i}(\bar{X_i} - \bar{X})^2\)
Partição dos graus de liberdade
Correspondendo à partição da soma total dos quadrados dos desvios (SQTot), há uma partição dos respectivos graus de liberdade.
A SQTot possui \(n_{T} - 1\) graus de liberdade associado a ela. Há \(n_{T}\) desvios \(X_{ij} - \bar{X}\), mas um grau de liberdade é perdido, porque esses desvios não são independentes, já que a soma de todos eles é 0.
A SQE possui \(n_{T} - k\) graus de liberdade associado a ela. Em cada amostra, há \(n_{i}\) desvios, mas um grau de liberdade é perdido, porque esses desvios não são independentes, já que a soma dos desvios em relação média de cada amostra é nula. Então o número de graus de liberdade é igual a \(\sum_{i=1}^{k}{(n_{i}-1)}\) = \(n_{T} - k\).
A SQEG possui k - 1 graus de liberdade associado a ela. Há k desvios das médias de cada amostra em relação à média geral, mas um grau de liberdade é perdido, porque esses desvios não são independentes, já que a soma dos desvios das médias de cada grupo em relação à média geral é igual a 0.
O erro quadrático médio residual (EQMR) é obtido dividindo-se a soma dos quadrados dos resíduos (SQE) por \(n_{T} - k\):
\[\begin{align} EQMR = \frac{\sum_{i=1}^{k}\sum_{j=1}^{n_{i}}(X_{ij} - \bar{X_i})^2}{n_{T} - k} \tag{18.5} \end{align}\]
O erro quadrático médio entre grupos (EQMEG) é obtido dividindo-se a soma dos quadrados entre grupos por k - 1:
\[\begin{align} EQMEG = \frac{\sum_{i=1}^{k}n_{i}(\bar{X_i} - \bar{X})^2}{k-1} \tag{18.6} \end{align}\]
Pode-se mostrar que o valor esperado do erro quadrático médio residual é igual à variância das populações:
\[\begin{align} E[EQMR] = \sigma^2 \tag{18.7} \end{align}\]
e que o valor esperado do erro quadrático médio entre grupos é igual à expressão abaixo:
\[\begin{align} E[EQMEG] = \sigma^2 + \frac{\sum_{i=1}^{k}n_{i}{(\mu_{i} - \mu)}^2}{k-1} \tag{18.8} \end{align}\]
Teste F
Quando a hipótese nula é verdadeira, tanto o erro quadrático médio residual quanto o erro quadrático médio entre grupos são estimadores não tendenciosos da variância das populações. Quando a hipótese nula não é verdadeira, o valor esperado do erro quadrático médio entre grupos é maior do que a variância das populações, aumentando à medida que as diferenças entre as médias das populações aumenta.
Assim a divisão do valor do erro quadrático médio entre grupos (EQMEG) pelo erro quadrático médio residual (EQMR) dá uma indicação de quanto a hipótese nula é compatível com os dados. O valor dessa divisão é representado por \(F^*\):
\[\begin{align} F^* = \frac{EQMEG}{EQMR} \tag{18.9} \end{align}\]
Pode-se mostrar que a razão \(\frac{EQMEG}{EQMR}\), se a hipótese nula é verdadeira, segue a distribuição de Fisher, F(k - 1, \(n_{T} - k\)). A distribuição F(\(\nu_{1}\), \(\nu_{2}\)) possui dois parâmetros onde \(\nu_{1}\) é o número de graus de liberdade do numerador e \(\nu_{2}\) é o número de graus de liberdade do denominador. Dado um nível de significância \(\alpha\), quando o valor de F, obtido da expressão (18.9) for maior que o quantil 1 - \(\alpha\) da distribuição F(k - 1, \(n_{T} - k\)), então a hipótese nula é rejeitada.
Esse método é conhecido por análise de variância, porque é realizada a comparação das variâncias cujas estimativas são obtidas pelas expressões (18.5) e (18.6) para verificar se as médias das populações correspondentes a cada nível do fator em estudo são diferentes ou não.
A aplicação Análise de Variância (figura 18.5) ilustra a ideia básica da análise de variância. O painel à esquerda permite ao usuário configurar a média e o tamanho das amostras de cada nível do fator em estudo (3 níveis na aplicação), o desvio padrão comum a cada distribuição dos valores da variável aleatória e o nível de significância do teste estatístico. O painel principal mostra, no primeiro gráfico, a média em cada grupo (indicados pelas cores preta, vermelha e verde) e as distâncias entre cada valor da variável aleatória e a correspondente média de cada grupo. O gráfico superior à direita mostra para cada valor da variável aleatória para um dado grupo a distância entre a média do grupo e a média geral. O gráfico na parte inferior da figura mostra a distância de cada valor da variável aleatória e a média geral. Finalmente a tabela na área inferior à direita mostra os cálculos para a análise de variância.
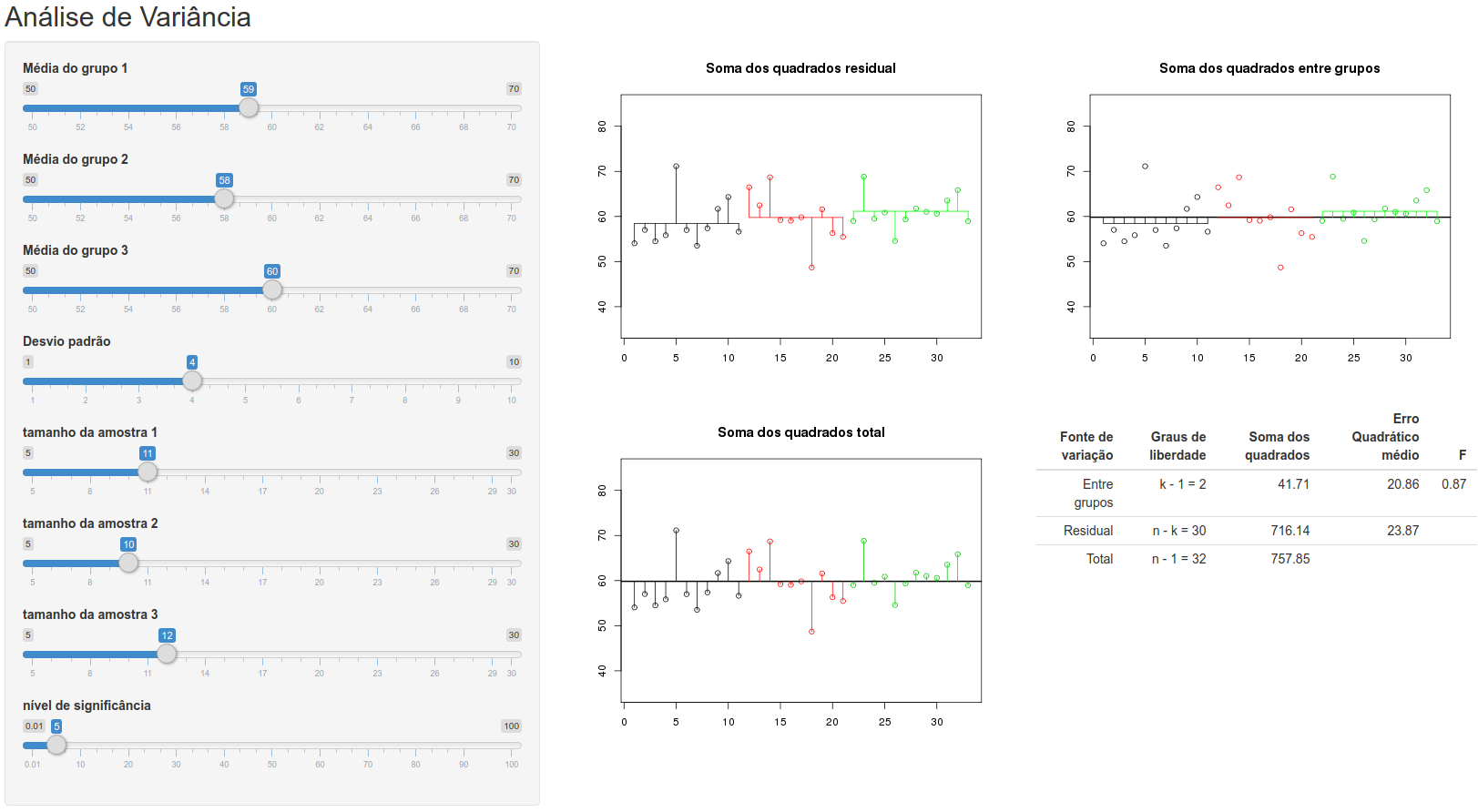
Figura 18.5: Aplicação que ilustra o princípio da ANOVA.
Quando as médias amostrais dos grupos são próximas (figura 18.6: médias amostrais iguais a 59, 58 e 60 em cada grupo, respectivamente) e com o desvio padrão igual a 4, por exemplo, as estimativas da variância por meio da soma dos quadrados dos resíduos e pela soma dos quadrados entre grupos (com tamanhos de amostras iguais a 11, 12 e 11, respectivamente) não são muito diferentes. O valor de F não é estatisticamente significativo.
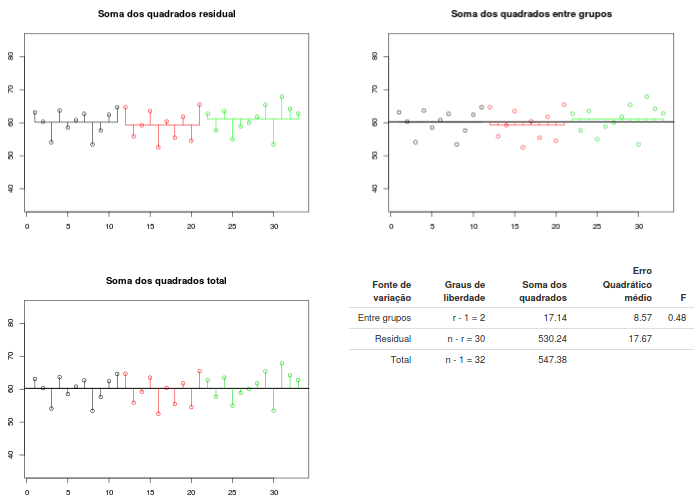
Figura 18.6: Variâncias obtidas na aplicação da figura 18.5 quando as médias são próximas.
Quando as médias amostrais dos grupos não são próximas (figura 18.7: médias amostrais iguais a 69, 50 e 60 em cada grupo, respectivamente) e com o mesmo desvio padrão (4), as estimativas da variância por meio da soma dos quadrados dos resíduos e pela soma dos quadrados entre grupos (com tamanhos de amostras iguais a 11, 10 e 12, respectivamente) são bem diferentes. O valor de F é estatisticamente significativo, indicado por um asterisco após a letra F no gráfico.
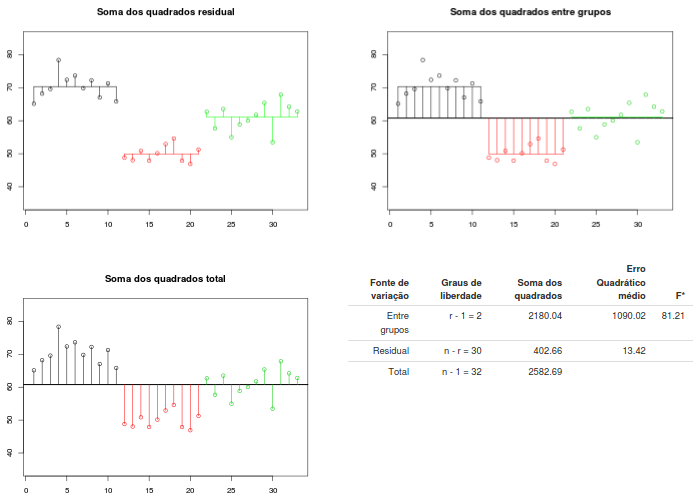
Figura 18.7: Variâncias obtidas na aplicação da figura 18.5 quando as médias são significativamente diferentes.
18.3.3 Comparação de médias
Os conteúdos desta seção e das subseções 18.3.3.1 e 18.3.3.2 podem ser visualizados neste vídeo.
Quando uma análise de variância rejeita a hipótese nula de igualdade de médias, ou mesmo na ausência de um teste de hipótese, em geral há interesse em obter intervalos de confiança para a diferença de médias entre os diversos grupos que compõem o estudo.
Na seção 18.2, vimos que realizar comparações de médias duas a duas por meio do teste t acaba gerando um nível de significância bem acima do nível de significância de uma única comparação. O mesmo ocorre para múltiplos intervalos de confiança, cada um deles calculado com um nível de confiança \(1 - \alpha\): a cobertura de todos os intervalos de confiança construídos é menor do que \(1 - \alpha\).
Há diversos procedimentos propostos na literatura estatística para lidar com esse problema, conhecido como múltiplas comparações. Alguns métodos frequentemente citados são: Bonferroni, Scheffé, Tukey e Newman-Keuls. Nesta seção, apresentaremos os métodos de Bonferroni, Tukey e Scheffé.
Vamos supor que desejamos obter o intervalo de confiança para a diferença das médias dos grupos i e j, \(\mu_i - \mu_j\), com amostras de tamanho ni e nj respectivamente. A estimativa para a diferença das médias é dada por:
\({\bar{D}}_{ij}=\bar{X_i}-\bar{X_j}\),
e a variância para a diferença das médias, supondo que a distribuições das variáveis Xi e Xj sejam normais, ou que as amostras sejam suficientemente grandes, será dada por:
\[\begin{align} var({\bar{D}}_{ij}) = var(\bar{X_i})+var(\bar{X_j})= \sigma^2 \left(\frac{1}{n_i}+\frac{1}{n_j}\right) \end{align}\]
Logo o erro padrão para as diferenças das duas médias é dado por:
\[\begin{align} EP({\bar{D}}_{ij}) =\sigma \sqrt{\frac{1}{n_i}+\frac{1}{n_j}} \end{align}\]
e é estimado por:
\[\begin{align} EP({\bar{D}}_{ij}) = \sqrt{EQMR (\frac{1}{n_i}+\frac{1}{n_j})} \tag{18.10} \end{align}\]
O intervalo de confiança ao nível de (\(1 - \alpha\))% para a diferença das médias \(\mu_i\) – \(\mu_j\) é então dado por:
\[\begin{align} {\bar{D}}_{ij}-t_{n_i+n_j-2, 1-\alpha/2}\ EP({\bar{D}}_{ij})\ \leq (\mu_i - \mu_j) \leq\ {\bar{D}}_{ij}+t_{n_i+n_j-2, 1-\alpha/2}\ EP({\bar{D}}_{ij}) \tag{18.11} \end{align}\]
Os diversos procedimentos para lidar com múltiplas comparações de médias substituem o elemento \(t_{n_i+n_j-2, 1-\alpha/2}\) na expressão acima por outro valor de modo a que o conjunto de comparações realizadas tenha pelo menos um grau de confiança \(1 - \alpha\) %. Os intervalos de confiança serão mais largos do que os obtidos com uma só comparação.
Esses métodos são particularmente importantes quando o interesse reside em realizar comparações que foram pensadas após uma inspeção dos dados e que não foram planejadas a priori, antes da realização do estudo. Em investigações exploratórias, muitas questões novas podem ser sugeridas quando os dados são analisados.
18.3.3.1 Método de Bonferroni
O método de Bonferroni é o mais simples de todos: no termo \(t_{n_i+n_j-2, 1-\alpha/2}\), divide-se o valor de \(\alpha/2\) pelo número de comparações realizadas. Assim, se o número de grupos for 3 e se deseja o intervalo de confiança para a diferença de todas as médias entre si, então substitui-se \(t_{n_i+n_j-2, 1-\alpha/2}\) na expressão (18.11) por \(t_{n_i+n_j-2, 1-\alpha/6}\).
À medida que o número de comparações aumenta, os intervalos de confiança ficam excessivamente conservadores no sentido de que o nível de confiança é na verdade maior do que \((1 - \alpha)\%\).
18.3.3.2 Método de Tukey
O método de Tukey pode ser utilizado quando se deseja comparar as médias de todos os pares de níveis do fator em estudo, ou seja, quando se deseja estimar \({\bar{D}}_{ij} = \mu_i - \mu_j\) para todos os pares i, j.
Quando os tamanhos das amostras são iguais, o nível de confiança para toda a família de comparações é exatamente \((1 - \alpha)\%\). Quando as amostras não são iguais, o nível de confiança da família de intervalos é maior que \((1 - \alpha)\%\).
O método de Tukey é baseado na distribuição da estatística conhecida como amplitude studentizada (studentized range), que é definida pela expressão:
\[\begin{align} q(k, \nu) =\frac{max(X_i)-min(X_i)}{s} \tag{18.12} \end{align}\]
onde Xi, i = 1, …, k corresponde a k observações independentes de uma distribuição normal com média \(\mu\) e variância \(\sigma^2\). Então o numerador da expressão acima corresponde à amplitude das k observações e s2 corresponde à estimativa da variância com \(\nu\) graus de liberdade.
Para a ANOVA com um fator, os intervalos de confiança para as diferenças entre pares de médias, de acordo com o método de Tukey, são obtidos substituindo-se \(t_{n_i+n_j-2, 1-\alpha/2}\) na expressão (18.11) por:
\[\begin{align} T =\frac{q(1-\alpha, k, n_T-k)}{\sqrt{2}} \tag{18.13} \end{align}\]
Os valores de T são então obtidos a partir do quantil \(1 - \alpha\) da distribuição de q com parâmetros iguais a k (número de níveis do fator – grupos) e nT – k, respectivamente (nT é o número total de observações).
18.3.3.3 Método de Scheffé
O método de Scheffé se aplica quando se deseja estimativas de intervalos de confiança para o conjunto de todos os contrastes possíveis entre as médias dos níveis do fator em estudo.
Um contraste é uma expressão da forma:
\(C = \sum c_k \mu_k\), onde \(\sum c_k = 0\).
Um exemplo de um contraste para três níveis de um fator seria: \(\frac{\mu_1+\mu_2}{2}-\mu_3\)
Uma estimativa de um contraste é dada por:
\[\begin{align} \bar{C} = \sum c_k \bar{X_k} \tag{18.14} \end{align}\]
Uma estimativa da variância de um contraste é dada por:
\[\begin{align} var(\bar{C}) = EQMR\ \sum \frac{c_k^2} {n_k} \tag{18.15} \end{align}\]
Pode-se mostrar que a probabilidade é (\(1 - \alpha\))% de que todos os intervalos do tipo:
\(\bar{C} \pm S\ var(\bar{C})\)
estejam corretos simultaneamente, onde \(\bar{C}\) e \(var(\bar{C})\) são calculados por (18.14) e (18.15), respectivamente, e S é dado por:
\(S^2 = (k-1) F(1 - \alpha, k - 1; n_T - 1)\)
O método de Scheffé é mais flexível do que os demais, porque permite obter intervalos de confiança com o nível de confiança \((1 - \alpha)\)%, quando considerados simultaneamente, para um conjunto muito mais amplo de comparações. Por essa razão, as amplitudes dos intervalos de confiança, em geral, são maiores do que intervalos de confiança obtidos por outros métodos. Quando se deseja realizar poucas comparações, possivelmente os métodos de Bonferroni, Tukey e outros podem fornecer intervalos mais precisos.
18.3.4 Análise de resíduos
Os conteúdos desta seção, de suas subseções e da seção 18.3.5 podem ser visualizados neste vídeo.
A análise de variância apresentada nas seções anteriores parte de três suposições básicas:
as variâncias da variável resposta são as mesmas em todos os grupos;
os erros são distribuídos normalmente;
os erros são independentes.
Os desvios, ou resíduos, das observações em relação à média em cada grupo ou nível do fator em estudo
\[\begin{align} r_{ij}=X_{ij} - \bar{X_i},\ \ \ i = 1, 2, \dots, n_i \tag{18.16} \end{align}\]
podem ser usados para checar se as suposições acima são satisfeitas. Essa análise é conhecida como análise de resíduos.
18.3.4.1 Comparação das variâncias
A igualdade das variâncias da variável resposta em cada nível do fator em estudo pode ser investigada qualitativamente, por exemplo, por um diagrama de pontos que mostram os resíduos para cada nível do fator. A figura 18.8 mostra dois diagramas de resíduos para cada um dos quatro níveis de um fator. No diagrama a, é possível observar que a variabilidade dos dados é diferente nos diversos níveis do fator, enquanto que no diagrama b não é possível identificar claramente uma divergência nos valores das variâncias em cada grupo.
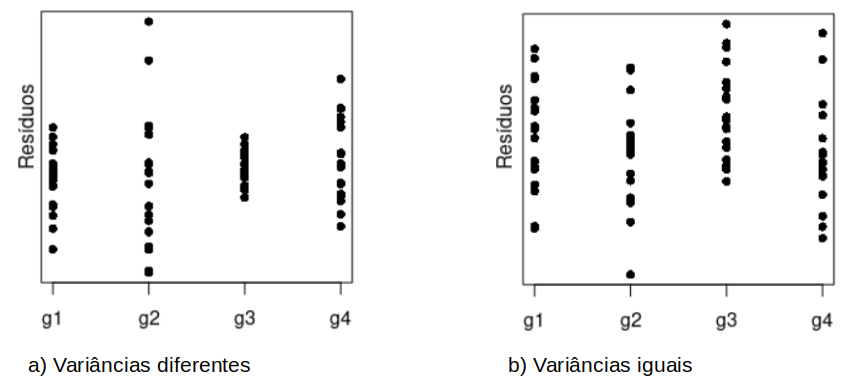
Figura 18.8: Variância de uma variável em quatro grupos diferentes e duas situações: a) variâncias diferentes e b) variâncias iguais.
A igualdade de variâncias também pode ser testada por meio de diversos testes estatísticos como Bartlett, Levene, etc. Não vamos entrar em detalhes desses testes neste texto, mas vamos ver como realizá-los no R na seção 18.3.6.
18.3.4.2 Avaliação da normalidade dos dados
A avaliação da normalidade dos dados é realizada, por exemplo, plotando o gráfico de comparação dos quantis da normal para os resíduos obtidos a partir da expressão (18.16) (capítulo 16, seção 16.2.3), e/ou realizando um teste de normalidade dos resíduos (capítulo 16, seção 16.2.4).
Deve-se levar em conta que a ANOVA é robusta para desvios não muito acentuados da normalidade e da igualdade de variâncias.
Mais adiante, na seção 18.3.6.1, será mostrado como avaliar a normalidade dos resíduos de um modelo de ANOVA com um fator.
18.3.4.3 Independência dos erros
Em relação ao terceiro item, independência dos resíduos, quando os dados são obtidos em uma sequência temporal ou quando os dados estão ordenados em uma outra lógica sequencial, como, por exemplo, uma sequência espacial, deve-se verificar se os resíduos não estão relacionados de alguma forma. Um diagrama dos resíduos versus ordenação dos mesmos para cada nível do fator em estudo é útil para identificar algum padrão de relacionamento. A figura 18.9 mostra três possíveis diagramas que relacionam os resíduos com uma possível sequência lógica em que as observações foram medidas, sendo que os dois primeiros diagramas mostram claramente um padrão linear e não linear entre os resíduos e a ordem em que foram obtidos, respectivamente. O diagrama c mostra o caso em que os resíduos não são relacionados uns com os outros.
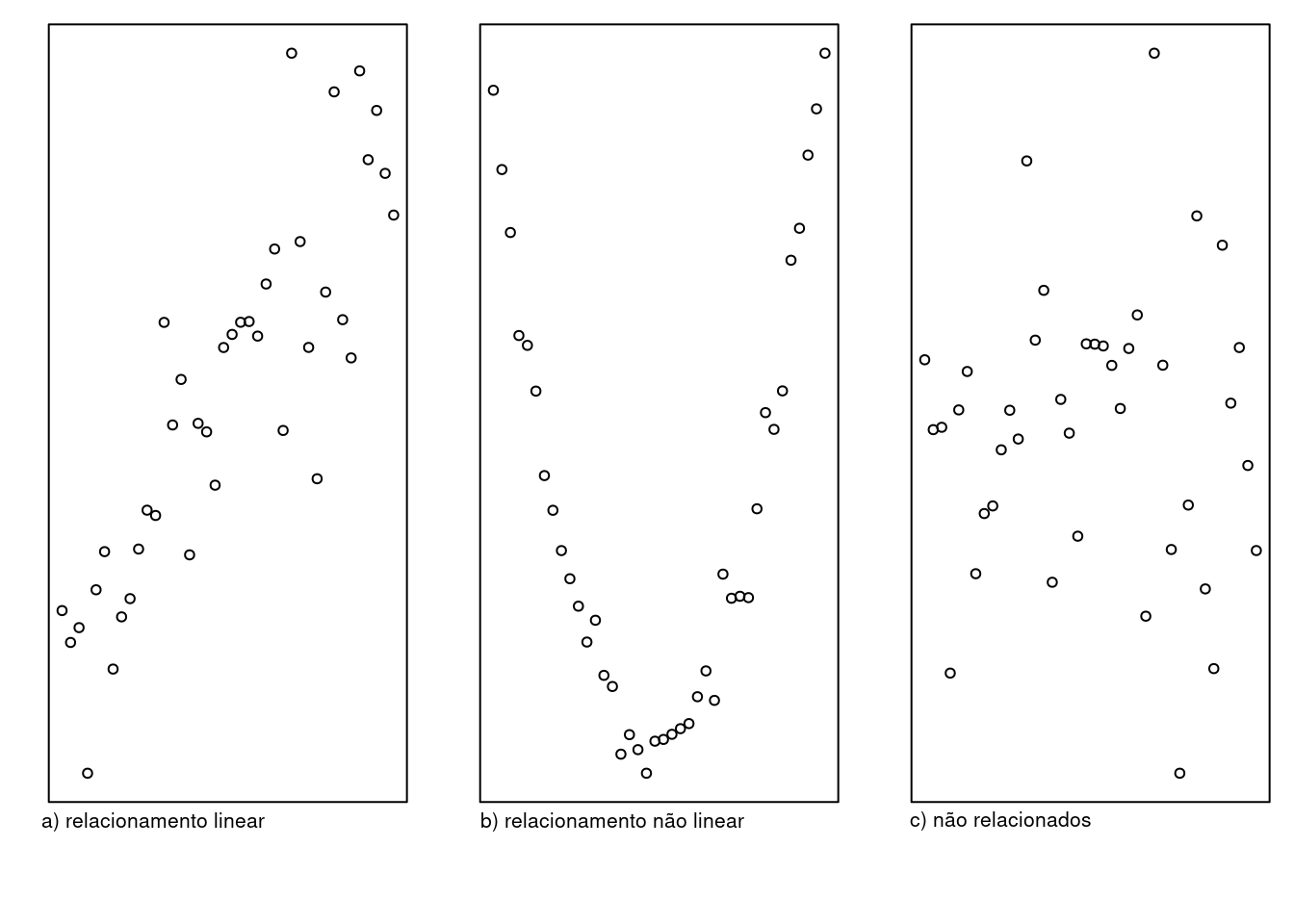
Figura 18.9: Diagramas que relacionam os resíduos com uma possível sequência lógica em que as observações foram medidas. O diagrama c mostra o caso em que os resíduos não são relacionados uns com os outros, enquanto que os diagramas a e b mostram relacionamentos linear e não linear, respectivamente..
18.3.5 Teste não paramétrico de Kruskal-Wallis
Se o modelo da análise de variância com um fator apresenta grandes desvios da normalidade ou da igualdade das variâncias dos grupos, um teste não paramétrico pode ser empregado para testar a hipótese nula de igualdade de médias entre os diversos grupos de tratamento. Um teste bastante utilizado é o teste de Kruskal-Wallis, que parte das seguintes suposições:
a distribuição da variável resposta em cada um dos grupos são contínuas e com a mesma forma, ou seja, possuem a mesma variabilidade, simetria, etc., mas podem diferir na localização da média;
as amostras dos diferentes grupos são aleatórias e independentes.
O teste de Kruskal-Wallis parte de todas as nT observações, que são então ordenadas de 1 a nT. Seja \(\bar{R_i}\) a média dos postos para o nível i do fator em estudo. A estatística para o teste de Kruskal-Wallis é então:
\[\begin{align} \chi_{kw}^2 = \left(\frac{12}{n_T(n_T+1)} \sum_{i=1}^{k} n_i \bar{R_i^2} \right) -3(n_T+1) \tag{18.17} \end{align}\]
Se os ni forem razoavelmente grandes (5 ou mais é usualmente recomendado), a estatística (18.17) é uma variável aleatória com aproximadamente uma distribuição \(\chi^2\) com k-1 graus de liberdade quando a hipótese nula de que todas as médias são iguais é verdadeira. Valores suficientemente grandes de \(\chi_{kw}^2\) levam à rejeição de H0, ou seja, se \(\chi_{kw}^2 > \chi_{1-\alpha, k-1}^2\) , então H0 é rejeitada.
O teste de Kruskal-Wallis é mais poderoso do que a análise de variância paramétrica, quando os desvios da normalidade são grandes, mas possui um menor poder estatístico quando as condições para a aplicação do modelo de análise de variância forem satisfeitas.
Múltiplas comparações dos postos pós-teste podem ser realizadas, com diversos tipos de correções, analogamente ao usado para a ANOVA.
18.3.6 Análise de variância com um fator no R
Os conteúdos desta seção e de suas subseções podem ser visualizados neste vídeo.
Vamos realizar uma análise de variância para o problema colocado na introdução deste capítulo. Queremos saber se as médias de ácido fólico para os três métodos de ventilação no conjunto de dados red.cell.folate são diferentes ou não e quais são os intervalos de confiança para as diferenças de médias entre os tratamentos.
Após termos carregado o conjunto de dados red.cell.folate, para realizarmos a ANOVA para um fator no R Commander, é preciso selecionar a opção:
\[\text{Estatísticas} \Rightarrow \text{Médias} \Rightarrow \text{ANOVA para um fator (one-way)...}\]
Ao selecionarmos o item ANOVA para um fator, devemos escolher a variável que define os grupos de estudo e a variável resposta (figura 18.10). Nessa figura, também foi marcada a opção comparação de médias 1 a 1 para obtermos os intervalos de confiança para as diferenças de médias entre os grupos. Não marcamos a opção para realizar o teste com a suposição de que as variâncias fossem diferentes. Os resultados da análise de variância serão armazenados no objeto AnovaModel.1, que será utilizado depois para gerar os diagnósticos gráficos e numéricos do modelo. Esse nome pode ser alterado pelo usuário.
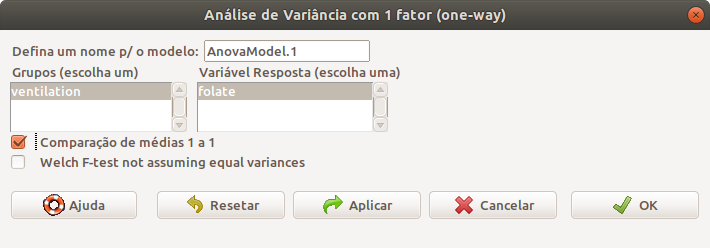
Figura 18.10: Seleção da variável que define os grupos e da variável resposta. Foi selecionada a opção para realizar a comparação de todos os pares de médias.
Os resultados são apresentados nas figuras 18.11 a 18.13. A figura 18.11 mostra o resumo do teste de hipótese, com o valor de p igual a 0,0436, estatisticamente significativo, quando o nível de significância escolhido é 5%. Logo abaixo são apresentados as médias, os desvios padrões e o número de elementos de cada método de ventilação.
A figura 18.12 mostra na porção inferior as diferenças de médias para cada par de métodos, assim como os limites inferior (lwr) e superior (upp) dos intervalos de confiança, usando o método de Tukey. A figura 18.13 mostra as três comparações de médias entre os métodos de modo gráfico. A única comparação que foi significativa ao nível de 5% foi a do N2O-O2, op e N2O-O2, 24h. As amplitudes dos intervalos de confiança são bastante elevadas, devido ao tamanho das amostras bastante pequeno.
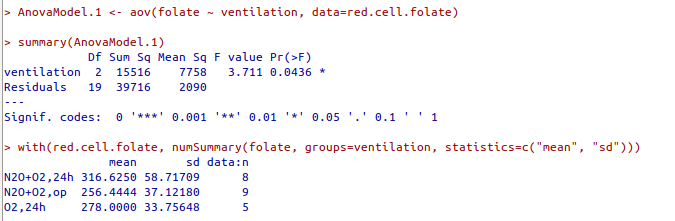
Figura 18.11: Resultados da análise de variância para a configuração da figura 18.10. O valor de p é igual 0,0436, indicando uma significância estatística limítrofe ao nível de 5%.

Figura 18.12: Continuação dos resultados da análise de variância para a configuração da figura 18.10. Na parte inferior, são apresentados os intervalos de confiança para cada par de grupos, usando o método de Tukey.
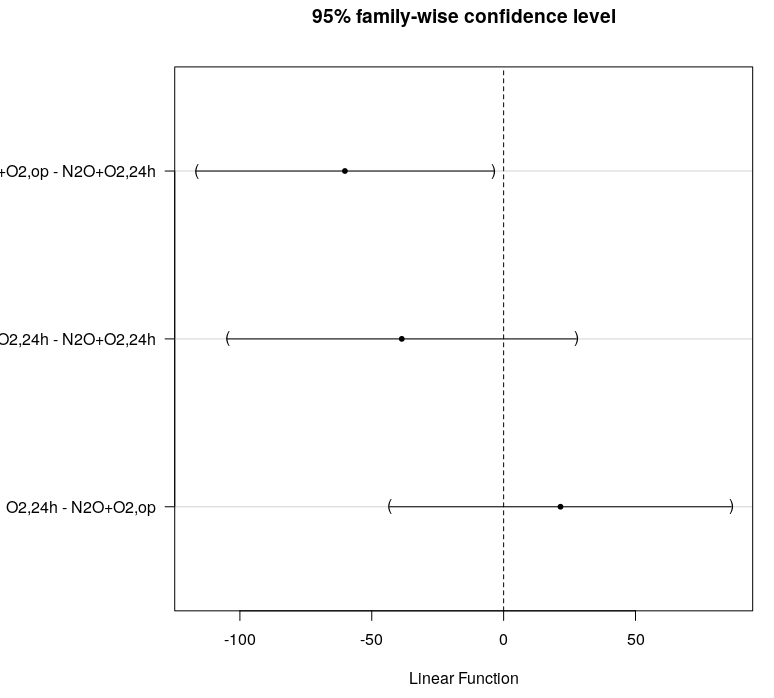
Figura 18.13: Diagrama que mostra os intervalos de confiança para as diferenças entre cada par de médias do ácido fólico, usando o método de Tukey.
Observem que o modelo AnovaModel.1 gerado por essa análise aparece selecionado ao lado do rótulo modelo, conforme indicado na figura 18.14.

Figura 18.14: R Commander com o modelo Anova.1 selecionado.
18.3.6.1 Avaliação da normalidade da variável resposta
Nesta seção, vamos construir o diagrama de comparação de quantis da normal e realizar um teste de normalidade para os resíduos do modelo de ANOVA gerado na seção anterior. Para isso, é necessário criar uma variável no conjunto de dados que irá conter os valores dos resíduos do modelo.
Certificando-nos que o modelo AnovaModel.1 esteja selecionado, os resíduos podem ser gerados por meio da opção:
\[\text{Modelos} \Rightarrow \text{Adicionar estatísticas calculadas aos dados}\]
De todas as opções que aparecem na tela da figura 18.15, vamos selecionar somente a opção Resíduos. Ao clicarmos em OK, os resíduos serão calculados e aparecem no conjunto de dados red.cell.folate como mais uma variável (figura 18.16).
Figura 18.15: Seleção das estatísticas que serão agregadas aos dados de red.cell.folate.
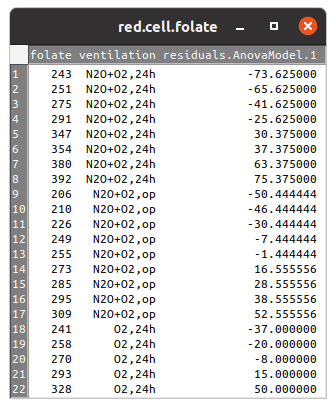
Figura 18.16: Conjunto de dados red.cell.folate após o cálculo dos resíduos.
Para gerar o gráfico de comparação de quantis no R Commander, usamos a seguinte opção:
\[\text{Gráficos} \Rightarrow \text{Gráfico de comparação de quantis...}\] Em seguida, selecionamos a variável residuals.AnovaModel.1 (figura 18.17). Ao clicarmos em OK, o gráfico é mostrado na figura 18.18, o qual indica que não há desvios significativos da hipótese de normalidade.
Figura 18.17: Seleção da variável para a construção do gráfico de comparação de quantis da normal.
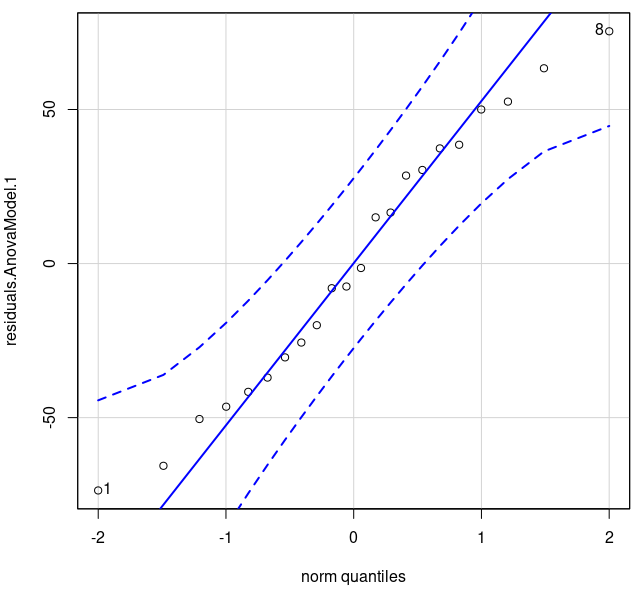
Figura 18.18: Diagrama de comparação dos quantis da normal para os resíduos do modelo.
Vamos agora realizar o teste de hipótese de normalidade de Shapiro-Wilk, acessando a opção:
\[\text{Estatísticas} \Rightarrow \text{Resumos} \Rightarrow \text{Test of normality...}\]
Em seguida, selecionamos a variável que desejamos testar, o teste de normalidade a ser realizado (figura 18.19) e clicamos em OK.
Figura 18.19: Seleção da variável e do teste de normalidade que será realizado.
O resultado é mostrado a seguir. O teste não rejeita a hipótese de normalidade ao nível de 5% (p = 0,62), em concordância com a inspeção visual do gráfico de comparação de quantis da normal.
normalityTest(~residuals.AnovaModel.1, test="shapiro.test",
data=red.cell.folate)##
## Shapiro-Wilk normality test
##
## data: residuals.AnovaModel.1
## W = 0.966, p-value = 0.618818.3.6.2 Diagnósticos gráficos do modelo
A figura 18.20 mostra o menu do R Commander para obter uma série de diagnósticos gráficos. Esses diagramas serão gerados para o modelo selecionado no item Modelo, na parte superior direita da tela (seta vermelha). Nesse exemplo, o modelo AnovaModel.1 foi gerado ao realizarmos a análise de variância para o conjunto de dados red.cell.folate.
Figura 18.20: Menu do R Commander para selecionar os diagnósticos gráficos básicos para a análise de variância.
Ao selecionarmos a opção diagnósticos gráficos básicos na figura 18.20 para o modelo selecionado, os resultados são apresentados na figura 18.21. Ao inspecionarmos os gráficos, particularmente o gráfico de resíduos (superior à esquerda) e o gráfico de comparação de quantis para os resíduos padronizados (superior à direita), não vemos grandes desvios da normalidade, mas as variãncias não parecem ser iguais. Resíduos padronizados são os resíduos divididos pela raiz quadrada do erro quadrático médio residual.
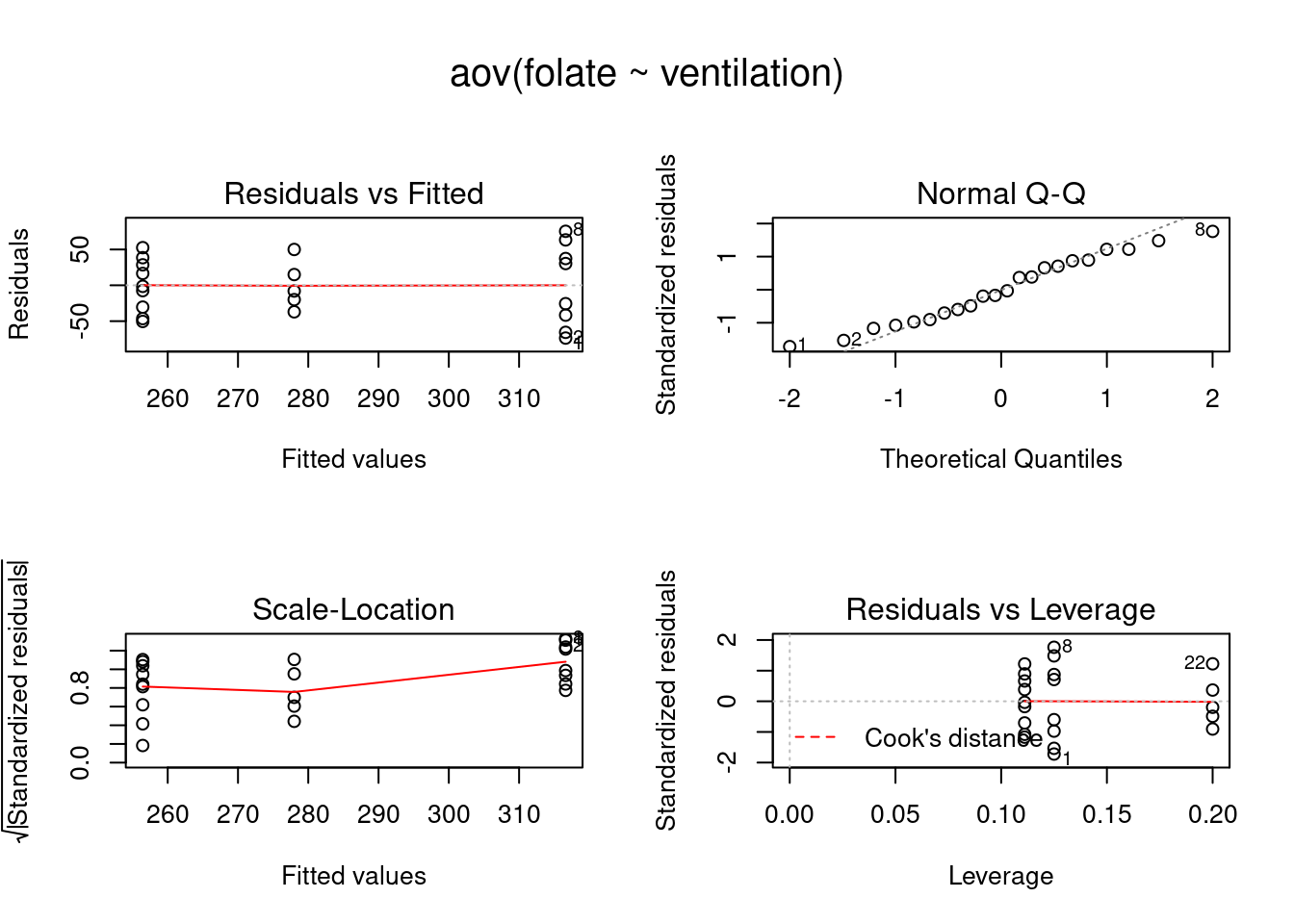
Figura 18.21: Diagnósticos gráficos básicos para a análise de variância do conjunto de dados red.cell.folate.
18.3.6.3 Testes para a igualdade de variâncias
Vamos realizar o teste de Levene para verificar a igualdade de variâncias, que pode ser acessado no R Commander por meio da opção:
\[\text{Estatísticas} \Rightarrow\ \text{Variâncias} \Rightarrow\ \text{Teste de Levene...}\]
Ao selecionarmos o teste, é preciso escolher a variável correspondente ao fator, a variável resposta e se o teste será baseado na média ou mediana (figura 18.22).
Figura 18.22: Configuração das variáveis para o teste de Levene para a comparação das variâncias da variável ácido fólico para os diversos métodos de ventilação.
O resultado é mostrado a seguir, indicando a rejeição da hipótese de igualdade de variâncias ao nível de 5% (p = 0,04).
with(red.cell.folate, tapply(folate, ventilation, var, na.rm=TRUE))## N2O+O2,24h N2O+O2,op O2,24h
## 3447.696 1378.028 1139.500leveneTest(folate ~ ventilation, data=red.cell.folate, center="mean")## Levene's Test for Homogeneity of Variance (center = "mean")
## Df F value Pr(>F)
## group 2 3.823 0.04024 *
## 19
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1O teste de Bartlett pode ser acessado no R Commander por meio da opção:
\[\text{Estatísticas} \Rightarrow\ \text{Variâncias} \Rightarrow\ \text{Teste de Bartlett}\]
Também precisamos selecionar a variável correspondente ao fator e a variável resposta (figura 18.23).
Figura 18.23: Seleção das variáveis para o teste de Bartlett para a comparação das variâncias da variável ácido fólico para os diversos métodos de ventilação.
O resultado é mostrado a seguir, não indicando a rejeição da hipótese de igualdade de variâncias ao nível de 5% (p = 0,35).
with(red.cell.folate, tapply(folate, ventilation, var, na.rm=TRUE))## N2O+O2,24h N2O+O2,op O2,24h
## 3447.696 1378.028 1139.500bartlett.test(folate ~ ventilation, data=red.cell.folate)##
## Bartlett test of homogeneity of variances
##
## data: folate by ventilation
## Bartlett's K-squared = 2.0951, df = 2, p-value = 0.3508Os testes de Levene e Bartlett produziram resultados conflitantes! Como as amostras são pequenas e a inspeção dos gráficos de diagnóstico sugere que as variâncias são diferentes, vamos realizar a ANOVA, supondo que as variâncias são diferentes.
18.3.6.4 Análise de variância quando as variâncias são diferentes
Ao marcarmos a opção Welch F-test not assuming equal variances na figura 18.10 (figura 18.24), a análise de variância será realizada de acordo com o método de Welch (Welch 1951).
Figura 18.24: Seleção da variável que define os grupos e da variável resposta para uma análise de variância, supondo que as variâncias sejam diferentes nos diferentes grupos.
Os resultados são mostrados na figura 18.25. Os intervalos de confiança para as diferenças de médias essencialmente não são alterados, mas a hipótese nula de igualdade de médias não é rejeitada ao nível de 5% (p =0,09).
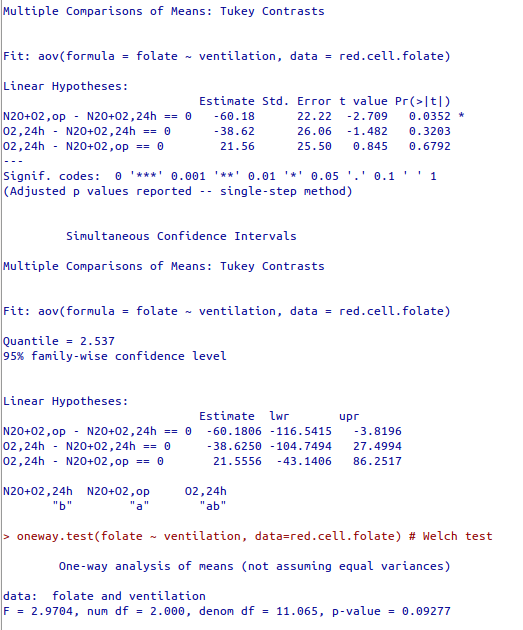
Figura 18.25: Resultados da análise de variância do ácido fólico para os diferentes métodos de ventilação, supondo que as variâncias sejam diferentes nos diferentes grupos.
18.3.6.5 Obtenção dos intervalos de confiança para a diferença de médias por outros métodos
A seção 18.3.6 calculou os intervalos de confiança para a comparação de médias duas a duas por meio do método de Tukey. A listagem abaixo mostra os comandos apresentados na janela de script do R Commander para gerar os resultados apresentados naquela seção.
library(mvtnorm, pos=17)
library(survival, pos=17)
library(MASS, pos=17)
library(TH.data, pos=17)
library(multcomp, pos=17)
library(abind, pos=22)
AnovaModel.1 <- aov(folate ~ ventilation, data=red.cell.folate)
summary(AnovaModel.1)
with(red.cell.folate, numSummary(folate, groups=ventilation,
statistics=c("mean", "sd")))
local({
.Pairs <- glht(AnovaModel.1, linfct = mcp(ventilation = "Tukey"))
print(summary(.Pairs)) # pairwise tests
print(confint(.Pairs)) # confidence intervals
print(cld(.Pairs)) # compact letter display
old.oma <- par(oma=c(0,5,0,0))
plot(confint(.Pairs))
par(old.oma)
}) Podemos alterar o comando que cria o objeto .Pairs para obtermos os intervalos de confiança segundo o método de Dunnet, por exemplo, que usa um grupo como referência e compara as médias dos demais grupos com a média do grupo de referência. Se alterarmos o comando, substituindo “Tukey” por “Dunnet”, conforme abaixo, e executarmos os dois comandos em sequência, obteremos dois intervalos de confiança, tomando o grupo N2O+O2,24h como referência. Observem que os dois intervalos são mais estreitos do que os obtidos pelo método de Tukey.
.Pairs <- glht(AnovaModel.1,
linfct = mcp(ventilation = "Dunnet")) # trocando Tukey por Dunnet
print(confint(.Pairs)) # intervalos de confiança##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Dunnett Contrasts
##
##
## Fit: aov(formula = folate ~ ventilation, data = red.cell.folate)
##
## Quantile = 2.3948
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## N2O+O2,op - N2O+O2,24h == 0 -60.1806 -113.3837 -6.9774
## O2,24h - N2O+O2,24h == 0 -38.6250 -101.0446 23.7946O pacote DescTools permite a utilização de outros métodos para lidar com o problema de múltiplas comparações. Os métodos disponíveis na função PostHocTest desse pacote são: hsd - Tukey, bonferroni, lsd, scheffe, newmankeuls, duncan. Apesar de constar nessa lista, muitos autores não recomendam o método de Duncan.
Para utilizarmos a função PostHocTest, primeiramente instalamos o pacote DescTools, caso não esteja instalado, e depois o carregamos.
install.packages(‘DescTools’)
library(DescTools)Em seguida, para obtermos intervalos ao nível de confiança de 95% com a correção de Bonferroni para a comparação de médias duas a duas, usamos a função a PostHocTest, lembrando que o objeto AnovaModel.1 foi gerado durante a realização da análise de variância. O argumento conf.level especifica o nível de confiança.
PostHocTest(AnovaModel.1, method = "bonferroni", conf.level = 0.95)##
## Posthoc multiple comparisons of means : Bonferroni
## 95% family-wise confidence level
##
## $ventilation
## diff lwr.ci upr.ci pval
## N2O+O2,op-N2O+O2,24h -60.18056 -118.49975 -1.86136 0.0418 *
## O2,24h-N2O+O2,24h -38.62500 -107.04688 29.79688 0.4643
## O2,24h-N2O+O2,op 21.55556 -45.38835 88.49947 1.0000
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Alterando o argumento method para scheffe na função PostHocTest, obtemos os intervalos de confiança para a comparação das médias de acordo com o método de Scheffé. A figura 18.26 mostra o gráfico dos intervalos de confiança para as diferenças de médias de ácido fólico entre os três métodos de ventilação, calculados de acordo com o método de Scheffé.
plot(PostHocTest(AnovaModel.1, method = "scheffe", conf.level = 0.95))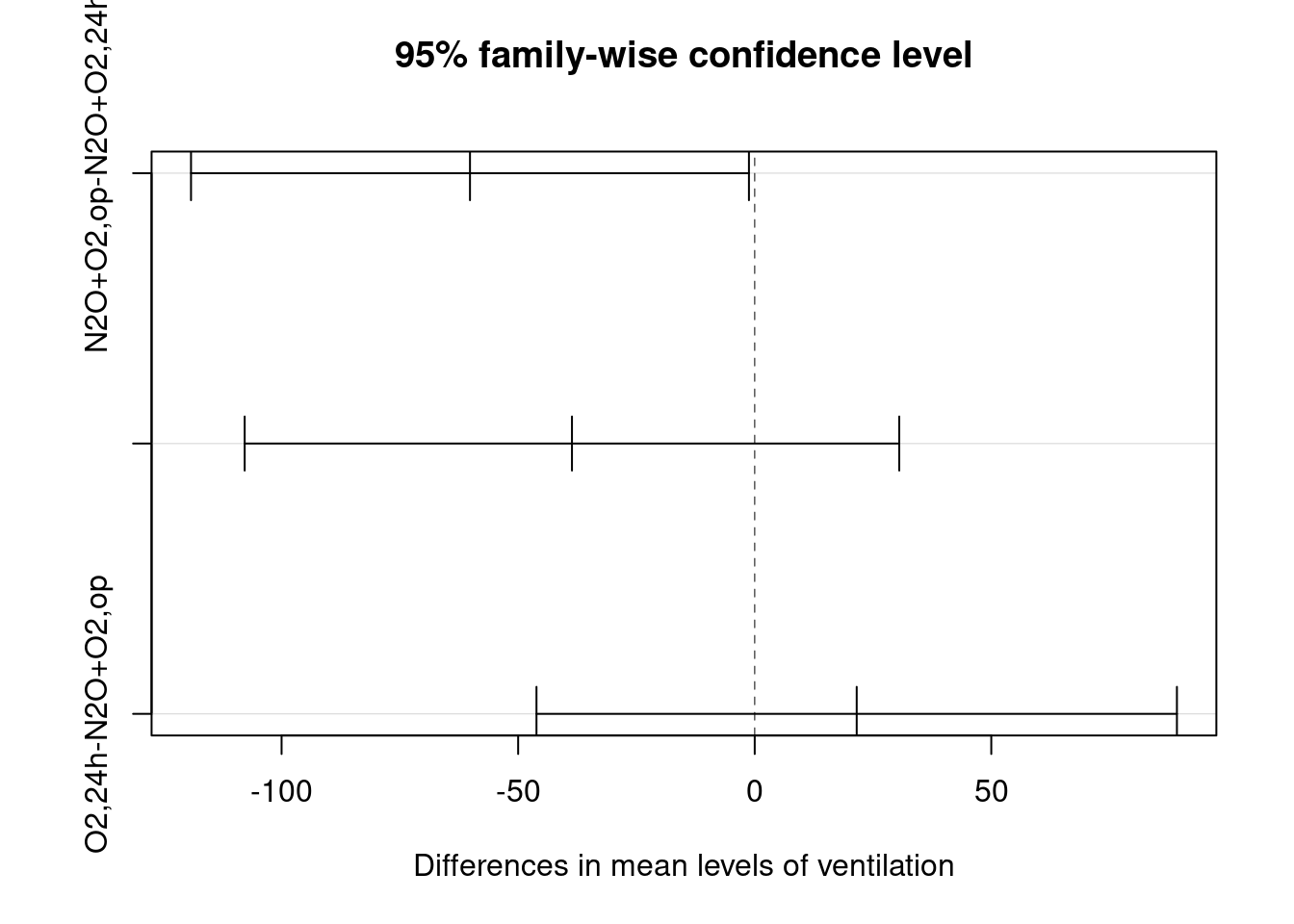
Figura 18.26: Intervalos de confiança da diferença de médias de ácido fólico entre os grupos de ventilação de acordo com o método de Scheffé.
Comparem os intervalos de confiança obtidos pelos diversos métodos mostrados nesta seção.
18.3.6.6 Teste de Kruskal-Wallis no R Commander
Vamos utilizar novamente o conjunto de dados red.cell.folate para realizar o teste de Kruskal-Wallis no R Commander. Dessa vez, vamos utilizar o RcmdrPlugin.EZR para realizarmos o teste de Kruskal-Wallis, porque ele oferece o recurso de realizar múltiplas comparações entre os diferentes grupos. Para carregarmos o plug-in RcmdrPlugin.EZR, selecionamos no menu Ferramentas a opção Carregar plug-in(s) do Rcmdr… (seção 17.4.1). Caso ele não apareça na lista de plug-ins, é preciso instalá-lo.
Após carregarmos o plug-in, selecionamos novamente o conjunto de dados red.cell.folate como o conjunto de dados ativo. Para realizarmos o teste de Kruskal-Wallis no R Commander, selecionamos a opção:
\[\text{Statistical analysis} \Rightarrow\ \text{Testes não paramétricos} \Rightarrow\ \text{Kruskal-Wallis test}\]
A figura 18.27 mostra a seleção das variáveis para o teste.
Figura 18.27: Seleção da variável que define os grupos e da variável resposta para o teste de Kruskal-Wallis.
Ao realizarmos a seleção das variáveis, o método de múltiplas comparações e pressionarmos o botão OK, os resultados são mostrados a seguir.
library(RcmdrPlugin.EZR)
tapply(red.cell.folate$folate, red.cell.folate$ventilation, median,
na.rm=TRUE)## N2O+O2,24h N2O+O2,op O2,24h
## 319 255 270res <- NULL
(res <- kruskal.test(folate ~ factor(ventilation), data=red.cell.folate))##
## Kruskal-Wallis rank sum test
##
## data: folate by factor(ventilation)
## Kruskal-Wallis chi-squared = 4.1852, df = 2, p-value = 0.1234pairwise.kruskal.test(red.cell.folate$folate, red.cell.folate$ventilation,
data.name="red.cell.folate", p.adjust.method="holm")##
## Pairwise comparisons using Mann-Whitney U test
##
## data: red.cell.folate
##
## N2O+O2,24h N2O+O2,op
## N2O+O2,op 0.18 -
## O2,24h 0.57 0.57
##
## P value adjustment method: holmO teste de Kruskal-Wallis não rejeita a hipótese nula de igualdade de médias (p=0,12). Observem como ele é menos poderoso do que o teste que utiliza o modelo da análise de variância. Nesse exemplo, as suposições para esse modelo são razoavelmente satisfeitas.
18.4 Análise de variância com medidas repetidas
Os conteúdos das subseções seguintes (subseções 18.4.1, 18.4.2, 18.4.3, 18.4.4 e 18.4.5) podem ser visualizados neste vídeo.
18.4.1 Modelo
Na análise de variância com um fator apresentada nas seções anteriores, observações independentes são realizadas para cada nível do fator em estudo. Ela é uma generalização do teste t para amostras independentes. Também existe uma generalização para o teste t pareado (amostras dependentes). No teste t pareado, por exemplo, para comparar as medidas de peso antes e depois de uma dieta para emagrecimento, uma única amostra de indivíduos pode ser coletada e medidas de peso são realizadas antes e depois do tratamento.
Em vez de apenas duas medidas de peso, poderíamos ter várias medidas realizadas antes do tratamento e após 30, 60 e 90 dias. Uma outra situação é quando três tratamentos diferentes são aplicados ao mesmo paciente em instantes diferentes e a variável resposta é medida após cada tratamento.
Nesses exemplos, o interesse está em saber se existe diferenças entre as médias após cada medida realizada. As unidades de observação (pacientes por exemplo) são chamadas de blocos, sendo as medidas realizadas em cada bloco e se supõe que as unidades de observação sejam extraídas aleatoriamente da população de interesse.
Da maneira usual, vamos chamar a variável que indica os instantes das medidas ou os tratamentos oferecidos de fator. Se os níveis do fator são diferentes instantes de tempo em que a variável resposta é medida, então o estudo é chamado de ANOVA com medidas repetidas.
Os comandos a seguir carregam e mostram o conjunto de dados heart.rate, do pacote ISwR, que contém dados de frequência cardíaca (hr) de 9 pacientes com insuficiência cardíaca antes (time = 0) e após a administração de enalaprilato (time = 30, 60 e 120 min). Cada um dos 9 pacientes apresenta valores de hr em cada um dos instantes de tempo. Nesse caso, diz-se que o estudo é balanceado. Se algum paciente não apresentasse todas as medidas, ou se apresentasse mais medidas do que os demais pacientes em algum instante de tempo, o estudo seria não balanceado.
data(heart.rate, package="ISwR")
heart.rate## hr subj time
## 1 96 1 0
## 2 110 2 0
## 3 89 3 0
## 4 95 4 0
## 5 128 5 0
## 6 100 6 0
## 7 72 7 0
## 8 79 8 0
## 9 100 9 0
## 10 92 1 30
## 11 106 2 30
## 12 86 3 30
## 13 78 4 30
## 14 124 5 30
## 15 98 6 30
## 16 68 7 30
## 17 75 8 30
## 18 106 9 30
## 19 86 1 60
## 20 108 2 60
## 21 85 3 60
## 22 78 4 60
## 23 118 5 60
## 24 100 6 60
## 25 67 7 60
## 26 74 8 60
## 27 104 9 60
## 28 92 1 120
## 29 114 2 120
## 30 83 3 120
## 31 83 4 120
## 32 118 5 120
## 33 94 6 120
## 34 71 7 120
## 35 74 8 120
## 36 102 9 120Vamos supor que temos k níveis do fator em estudo e que n unidades de observação serão avaliadas em cada nível do fator. O modelo para a análise de variância com medidas repetidas expressa a variável resposta nos seguintes componentes:
\[\begin{align} X_{ij} = \mu + \rho_i + \alpha_j + \epsilon_{ij} \tag{18.18} \end{align}\]
onde:
j - indica cada nível do fator em estudo (j = 1, 2, …, k).
i - indica cada uma das unidades de observação (por exemplo pacientes) (i = 1, 2, …, n).
Xij - valor da variável resposta correspondente ao nível j do fator para a unidade i.
\(\mu\) - média geral da variável X em todas os níveis do fator.
\(\alpha_j\) – constante que representa a diferença entre a média da variável X na população correspondente ao nível j do fator de estudo e a média geral. As constantes \(\alpha_j\) satisfazem a condição \(\sum_{j=1}^{k}\alpha_j = 0\).
\(\rho_i\) - componente que segue a distribuição \(N(0, \sigma_{\rho}^2)\) e reflete as características específicas de cada unidade de observação.
\(\epsilon_{ij}\) - erro associado ao valor j da unidade de observação i. Os erros seguem a distribuição \(N(0, \sigma^2)\).
\(\rho_i\) e \(\epsilon_{ij}\) são independentes.
Esse modelo é chamado de modelo III (níveis dos fatores misturados), porque as unidades de observação (sujeitos) são aleatórias (um subconjunto de todos as unidades possíveis) e os níveis do fator em estudo são fixos.
18.4.2 Teste de hipótese
Na análise de variância de modelos fixos com um fator, a hipótese nula para um teste bilateral é que as médias da variável resposta correspondentes a cada nível do fator são iguais e a hipótese alternativa é que pelo menos uma das médias é diferente das demais:
H0: \(\alpha_j = 0\), i = 1, 2, …, k
H1: nem todos os \(\alpha_j = 0\)
Para verificar a hipótese H0, vamos considerar a situação em que uma variável aleatória X foi medida em k níveis do fator em n indivíduos diferentes, sendo cada indivíduo submetido a todos os níveis do fator em estudo.
A média aritmética de todos os valores de X (média geral) é dada por:
\[\begin{align} \bar{X} = \frac{\sum_{j=1}^{k}\sum_{i=1}^{n} X_{ij}}{nk} \tag{18.19} \end{align}\]
A média aritmética dos valores de X para cada nível do fator é dada por:
\[\begin{align} {\bar{X}}_{.j} = \frac{\sum_{i=1}^{n} X_{ij}}{n}, \ \ \ \ \ \ \text{onde j = 1, 2, ..., k} \tag{18.20} \end{align}\]
A média aritmética dos valores de X para cada unidade de observação é dada por:
\[\begin{align} {\bar{X}}_{i.} = \frac{\sum_{j=1}^{k} X_{ij}}{k}, \ \ \ \ \ \ \text{onde i = 1, 2, ..., n} \tag{18.21} \end{align}\]
Partição da soma dos resíduos em relação à média geral
A expressão a seguir mostra que o desvio de cada valor da variável aleatória em relação à média geral é igual ao desvio da média do respectivo fator em relação à média geral somado ao desvio em relação à média geral da média da unidade de observação correspondente e um termo que representa a interação entre unidades de observação e os níveis do fator em estudo:
\(\begin{aligned} \underbrace{X_{ij} - \bar{X}}_\text{desvio em relação à média geral} &= \underbrace{({\bar{X}}_{.j} - \bar{X})}_\text{ desvio da média do nível do fator em relação à média geral} + \\ &\underbrace{({\bar{X}}_{i.} - \bar{X})}_\text{desvio da média da unidade de observação em relação à média geral} + \\ &\underbrace{(X_{ij} - {\bar{X}}_{.j} - {\bar{X}}_{i.} + \bar{X})}_\text{termo que descreve a interação entre unidades de observação e níveis do fator} \end{aligned}\)
Elevando cada desvio ao quadrado e somando os quadrados de todos os desvios, pode-se mostrar que o resultado é a expressão abaixo:
\(\begin{aligned} \sum_{j=1}^{k}\sum_{i=1}^{n}(X_{ij} - \bar{X})^2 = \sum_{j=1}^{k}\sum_{i=1}^{n}(\bar{X_{.j}} - \bar{X})^2 + &\sum_{j=1}^{k}\sum_{i=1}^{n}({\bar{X}}_{i.} - \bar{X})^2 + \\ &\sum_{j=1}^{k}\sum_{i=1}^{n}(X_{ij} - {\bar{X}}_{i.} - {\bar{X}}_{.j} + \bar{X})^2 \end{aligned}\)
Essa expressão pode ser escrita como:
\(SQTot = SQS + SQF + SQF.S\)
onde:
\(SQTot = \sum_{j=1}^{k}\sum_{i=1}^{n}(X_{ij} - \bar{X})^2\) representa a soma total dos quadrados, com nk-1 graus de liberdade.
\(SQF = n\sum_{j=1}^{k} ({\bar{X}}_{.j} - \bar{X})^2\) representa a soma dos quadrados para o fator, com k-1 graus de liberdade.
\(SQS = k\sum_{i=1}^{n}({\bar{X}}_{i.} - \bar{X})^2\) representa a soma dos quadrados para as unidades de análise, com n-1 graus de liberdade.
\(SQF.S = \sum_{j=1}^{k}\sum_{i=1}^{n}(X_{ij} - {\bar{X}}_{i.}- {\bar{X}}_{.j} + \bar{X})^2\) representa a soma dos quadrados da interação entre unidades de anaĺise e níveis do fator, com (k-1)(n-1) graus de liberdade
O erro quadrático médio da interação (EQMF.S) é obtido dividindo-se SQF.S pelo correspondente número de graus de liberdade:
\(EQMF.S = \frac{\sum_{j=1}^{k}\sum_{i=1}^{n}(X_{ij} - {\bar{X}}_{i.} - {\bar{X}}_{.j} + \bar{X})^2}{(n-1)(k-1)}\)
O erro quadrático médio do fator (EQMF) é obtido dividindo-se SQF pelo correspondente número de graus de liberdade:
\(EQMF = \frac{n\sum_{j=1}^{k} ({\bar{X}}_{.j} - \bar{X})^2}{k-1}\)
Pode-se mostrar que o valor esperado do erro quadrático médio da interação é igual à variância de \(\epsilon_{ij}\):
\(E[EQMF.S] = \sigma^2\)
e que o valor esperado do erro quadrático médio do fator é igual à expressão abaixo:
\(E[EQMF] = \sigma^2 + \frac{n\sum_{j=1}^{k} (\alpha_{j} - \mu)^2}{k-1}\)
Teste F
Quando a hipótese nula é verdadeira, tanto o erro quadrático médio da interação quanto o erro quadrático médio do fator são estimadores não tendenciosos da variância dos erros do modelo da ANOVA com medidas repetidas. Quando a hipótese nula não é verdadeira, o valor esperado do erro quadrático médio do fator é maior do que a variância de \(\epsilon_{ij}\), aumentando à medida que as diferenças entre as médias dos níveis dos fatores aumenta.
Assim a divisão do valor do erro quadrático médio do fator (EQMF) pelo erro quadrático médio da interação (EQMF.S) dá uma indicação de quanto a hipótese nula é compatível com os dados. O valor dessa divisão é representado por \(F^*\):
\[\begin{align} F^* = \frac{EQMR}{EQMF.S} \tag{18.22} \end{align}\]
Pode-se mostrar que a razão EQMR/EQMF.S, se a hipótese nula for verdadeira, segue a distribuição F(k-1, (k-1)(n-1)). Dado um nível de significância \(\alpha\), quando o valor de F*, obtido da expressão (18.22) for maior que o quantil (\(1-\alpha\)) da distribuição F(k-1, (k-1)(n-1)), então a hipótese nula é rejeitada.
18.4.3 Diagnósticos para verificar o modelo de medidas repetidas
Uma condição para que a estatística F* siga a distribuição F é que a variância da diferença entre as médias estimadas para dois níveis quaisquer do fator em estudo seja constante, ou seja:
\(\begin{aligned} &\ var({\bar{X}}_{i.}-{\bar{X}}_{.j})= \text{constante, } i \neq j \end{aligned}\)
Essa condição é conhecida como esfericidade. Alguns pacotes do R realizam um teste estatístico para verificar a condição de esfericidade e realizam ajustes no teste da ANOVA com medidas repetidas, quando a condição não é satisfeita.
Além disso, assim como na análise de variância com um fator, os erros devem possuir uma variância constante, serem independentes e normalmente distribuídos.
Diversos diagnósticos podem ser realizados para verificar se as condições para o modelo de análise de variância com medidas repetidas são satisfeitas, por exemplo:
um diagrama de interação, que mostra os valores da variável resposta por unidade de análise, pode ser examinado para verificar a interação entre unidades de observação e os níveis do fator em estudo;
um diagrama de comparação de quantis da normal dos resíduos. Os resíduos para o modelo de medidas repetidas apresentado nesta seção são dados por:
\(r_{ij} = X_{ij} - {\bar{X}}_{i.}- {\bar{X}}_{.j} + \bar{X}\)
um diagrama de pontos dos resíduos por níveis do fator em estudo para avaliar a constância da variância do erro;
diagramas da sequência de resíduos por unidade de análise podem ser úteis para verificar a constância da variância do erro e interferência de outros fatores. Esses gráficos são diagramas de dispersão dos resíduos x níveis do fator (se pudermos considerar que as medições para cada nível foram realizadas numa certa ordem), plotados separadamente para cada indivíduo;
um diagrama de comparação de quantis dos efeitos principais devido às unidades de análise, \(\bar{X_{i.}}-\bar{X}\), para avaliar se os efeitos devidos a \(\rho_i\) estão normalmente distribuídos. Os efeitos devido às unidades de análise são estimados pelos desvios da médias de cada indivíduo em relação à média geral.
Na seção 18.4.6, será mostrado como obter e interpretar os diagnósticos acima.
18.4.4 Intervalos de confiança
Para obtermos intervalos de confiança para contrastes entre as médias dos diversos níveis do fator em estudo, podemos utilizar os mesmos métodos apresentados na seção 18.3.3, utilizando o valor de EQMF.S como estimativa da variância dos erros do modelo.
Vamos considerar as diferenças entre dois pares de médias:
\({\bar{D}}_{lm}={\bar{X}}_{.l}-{\bar{X}}_{.m},\ \ l, m = 1, ...,k\)
A variância da diferença entre duas médias l e m, por exemplo, pode ser estimada por:
\(var({\bar{D}}_{lm})=var({\bar{X}}_{.l})+var({\bar{X}}_{.m}) = \frac {2} {n} EQMF.S\)
Logo o erro padrão da diferença entre duas médias l e m é:
\(EP({\bar{D}}_{lm}) = \sqrt{\frac{2}{n}EQMF.S}\)
18.4.5 Teste de Friedman
Quando as suposições para o modelo de análise de variância com medidas repetidas são seriamente violadas, um teste estatístico que pode ser realizado é o teste de Friedman. Nesse teste, os valores da variável resposta em cada um dos blocos (sujeitos ou unidades de observação) são ordenados e a cada um deles é atribuído um posto. Os postos são então somados para cada nível do fator, sendo Rj a soma dos postos para o fator j. A estatística
\(\chi_F^2 = \frac{12n}{k(k+1)} \sum_{j=1}^{k} (\bar{R_j}-\frac{k+1}{2})^2\), sendo \(\bar{R_j}=\frac{\sum_{i=1}^{n} R_{ij}}{n}\)
segue aproximadamente a distribuição qui ao quadrado com k-1 graus de liberdade, desde que o número de blocos não seja muito pequeno.
18.4.6 Análise de variância com medidas repetidas no R
O conteúdo desta subseção até a subseção seguinte (seção 18.4.6.1) pode ser visualizado neste vídeo.
Vamos utilizar o RcmdrPlugin.EZR para realizar a ANOVA com medidas repetidas para o conjunto de dados heart.rate.
Para usar o RcmdrPlugin.EZR para a análise com medidas repetidas, é preciso criar um data.frame onde cada uma das medidas repetidas apareçam em uma coluna separada (formato largo). Assim precisamos de 4 colunas, contendo as medidas de frequência cardíaca para cada indivíduo nos instantes 0, 20, 60 e 120 minutos. Para converter o conjunto de dados heart.rate no formato desejado, usamos a seguinte opção:
\[\text{Dados} \Rightarrow \text{Conjunto dados ativo} \Rightarrow \text{Reshape dataset from long to wide format...}\]
Na tela de configuração da transformação do conjunto de dados (figura 18.28), damos um nome para o conjunto de dados que será gerado (heart.rateWide), e selecionamos a variável que identifica cada indivíduo (subj), a variável resposta (hr - variables that vary by occasion) e o fator (time - within subject factors).
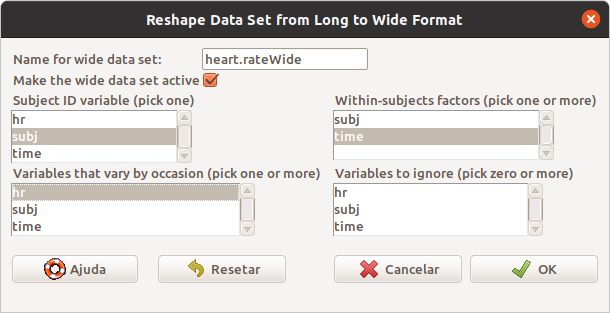
Figura 18.28: Diálogo para converter um data.frame do formato longo para o formato largo.
Ao clicarmos em OK, o comando a seguir é executado e o conjunto de dados heart.rateWide será criado a partir de heart.rate, com quatro variáveis (X0, X30, X60, X120) representando as medidas de frequência cardíaca para cada indivíduo nos instantes 0, 20, 60 e 120 minutos, respectivamente.
heart.rateWide <- reshapeL2W(heart.rate, within="time", id="subj",
varying="hr")Podemos, se for desejado, alterar os nomes das variáveis X0, X30, X60, X120 por meio da opção:
\[\text{Dados} \Rightarrow \text{Modificação de variáveis no conjunto de dados...} \Rightarrow \text{Renomear variáveis...}\]
Na tela mostrada na figura 18.29, selecionamos as variáveis que desejamos renomear. Ao clicarmos em OK, damos os novos nomes para as variáveis selecionadas (figura 18.30).
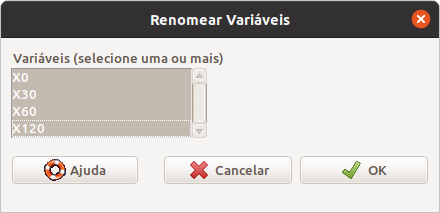
Figura 18.29: Seleção das variáveis a serem renomeadas no conjunto de dados heart.rateWide.
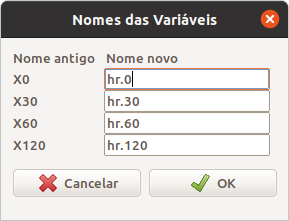
Figura 18.30: Fornecendo os novos nomes das variáveis selecionadas na figura 18.29.
Ao clicarmos em OK, o comando a seguir é executado, atribuindo os novos nomes das variáveis.
names(heart.rateWide)[c(1,2,3,4)] <- c("hr.0","hr.30","hr.60","hr.120")O comando a seguir exibe o conjunto de dados heart.rateWide. Agora os valores da frequência cardíaca de cada paciente são exibidos numa única linha.
heart.rateWide## hr.0 hr.30 hr.60 hr.120
## 1 96 92 86 92
## 2 110 106 108 114
## 3 89 86 85 83
## 4 95 78 78 83
## 5 128 124 118 118
## 6 100 98 100 94
## 7 72 68 67 71
## 8 79 75 74 74
## 9 100 106 104 102Para realizarmos a ANOVA com medidas repetidas no plugin RcmdrPlugin.EZR, acessamos a opção:
\[\text{Statistical analysis} \Rightarrow \text{Continuous variables} \Rightarrow \text{Repeated-measures ANOVA}\]
Na tela de configuração do teste (figura 18.31), selecionamos as variáveis que contêm as medidas de frequência cardíaca. Nesse exemplo, não há variável que separa os pacientes em grupos. Poderíamos realizar comparações par a par entre as médias de frequência cardíaca em cada instante, com correções de Holm ou Bonferroni, mas vamos realizar essas comparações de outra maneira, que mostra as diferenças e erros-padrão de cada comparação.
Os resultados do teste de hipótese são mostrados na figura 18.32, indicando que o valor de p (Pr(>F na figura)) é 0,01802 e rejeitando a hipótese nula de igualdade de médias para um nível de significância de 5%.
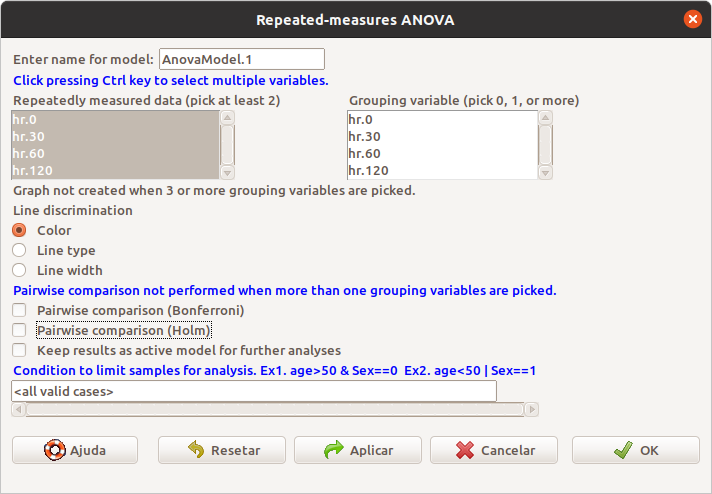
Figura 18.31: Seleção das medidas repetidas, configuração do gráfico de médias e comparação de pares de médias.
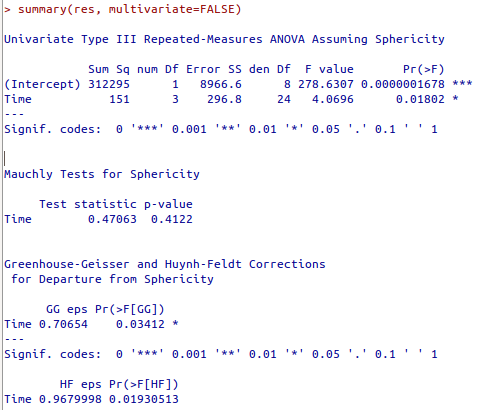
Figura 18.32: Resultados da análise de variância com medidas repetidas do conjunto de dados heart.rate.
Um teste de esfericidade (teste de Mauchly) não rejeitou a suposição de esfericidade. Mesmo assim, são apresentados os resultados de duas correções quando a suposição de esfericidade não é satisfeita: Greenhouse-Geisser epsilon (GGe), e Huynh-Feldt epsilon (HFe). As duas correções não alteram a significância estatística dos resultados (p = 0,034 e 0,019, respectivamente), caso tenha sido adotado o nível de significância de 5%.
A figura 18.33 mostra o gráfico de linhas das médias da frequência cardíaca em cada instante, indicando uma ligeira redução da média da frequência cardíaca após a administração do enalaprilato, ficando razoavelmente estável nos demais instantes.
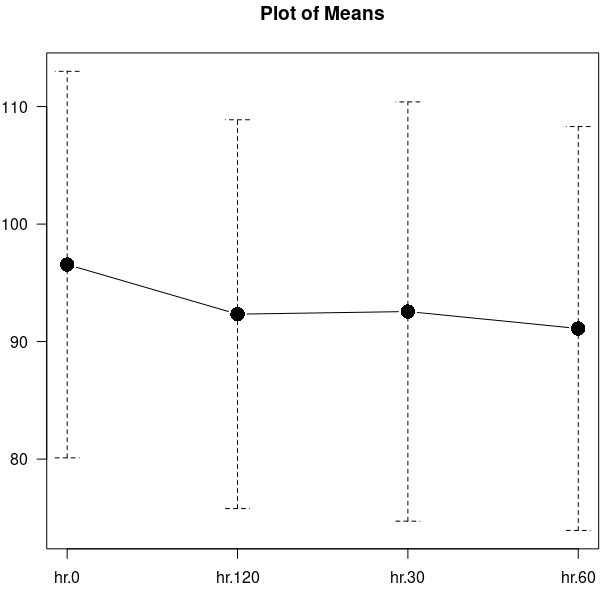
Figura 18.33: Diagrama de linha das médias das medidas de frequência cardíaca nos instantes 0, 30, 60 e 120 min.
Para verificarmos a interação entre as unidades de análise (pacientes) e o tempo de medição, ou seja, para verificarmos se os pacientes apresentam comportamentos diferentes de frequência cardíaca em relação ao tempo de medição, podemos gerar um diagrama de interação. Esse gráfico pode ser gerado por meio da seguinte opção:
\[\text{Graphs and tables} \Rightarrow \text{Line graph (Repeated measures)}\]
Na tela mostrada na figura 18.34, selecionamos as quatro variáveis que representam as medidas de frequência cardíaca nos quatro instantes diferentes e clicamos em OK. O diagrama de interação é mostrado na figura 18.35.
Figura 18.34: Seleção das variáveis que comporão o diagrama de interação entre pacientes e tempo de medição para a frequência cardíaca.
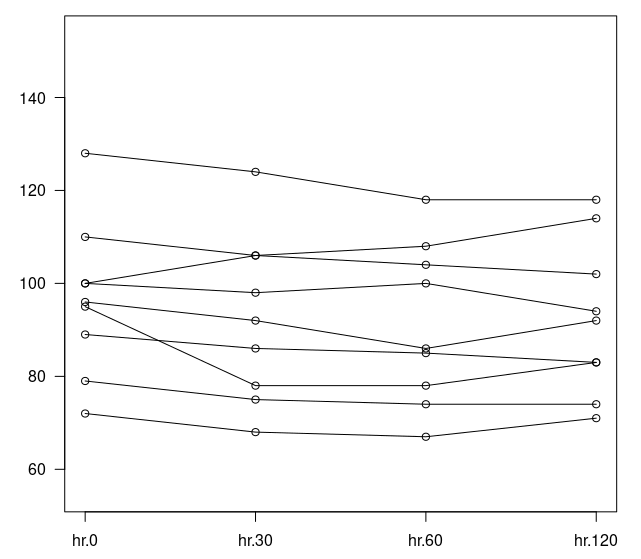
Figura 18.35: Diagrama de interação entre pacientes e tempo de medição para a frequência cardíaca, no conjunto de dados heart.rate.
O diagrama de interação une as medidas de frequência cardíaca para cada paciente por linhas. Nesse exemplo, temos 9 linhas correspondendo aos 9 pacientes. Podemos observar que, com uma única exceção, as linhas seguem um padrão de redução da frequência cardíaca do instante 0 até 120 min para cada paciente, com linhas razoavelmente paralelas, o que indica pouca interação entre os pacientes e o tempo. Caso as linhas dos pacientes seguissem padrões diferentes, isto indicaria que a frequência cardíaca apresentaria padrões diferentes de paciente para paciente.
Para realizarmos a comparação par a par das médias de frequência cardíaca em cada instante, podemos utilizar o script a seguir:
library(nlme)
library(multcomp)
am2 = lme(hr ~ time, random = ~1|subj, data=heart.rate)
.pairs = glht(am2,linfct=mcp(time="Tukey")) # múltiplas comparações
print(confint(.pairs)) # confidence intervals
old.oma <- par(oma=c(0,5,0,0))
plot(confint(.pairs), xlab = "Frequência cardíaca")
par(old.oma) Primeiramente, carregamos dois pacotes (nlme e multcomp). Pode ser necessário instalá-los antes de carregá-los. Em seguida, realizamos novamente a análise de variância com medidas repetidas por meio da função lme do pacote nlme. Para essa análise, usamos o conjunto de dados hear.rate original.
Para usarmos a função lme, precisamos especificar o conjunto de dados que será analisado (data = heart.rate) e uma fórmula que indica como a análise será realizada. A expressão hr ~ time indica que hr é a variável resposta, o símbolo ~ separa a variável resposta das variáveis independentes, sendo que time indica o fator, que é a variável independente. Essa expressão especifica os efeitos fixos do modelo, devido à variável time.
O argumento random = ~1|subj especifica o componente \(\rho_i\) do modelo. O termo ~1|subj indica que, a cada indivíduo (variável subj), corresponderá um valor aleatório que será adicionado à média geral, de acordo com o modelo (18.18).
O resultado da análise é armazenado em am2.
Em seguida, usamos a mesma sequência de comandos que foram usados no exemplo da ANOVA para um fator para o cálculo de intervalos de confiança para todos os pares de médias correspondentes aos níveis dos fator. Nesse caso, a função glht usa o objeto am2, resultado da análise de variância, e gera todas as diferenças entre as médias de hr nos diferentes instantes de tempo, por meio do método de Tukey. O resultado é armazenado no objeto .pairs.
O comando print(confint(.pairs)) imprime os intervalos de confiança para cada comparação de médias (figura 18.36).
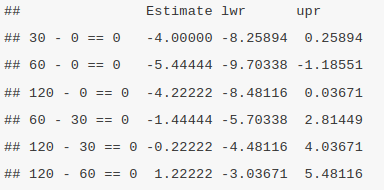
Figura 18.36: Intervalos de confiança para a comparação de médias de frequência cardíaca para cada par de instantes de tempo, usando o método de Tukey.
Finalmente o comando plot(confint(.pairs)) gera um gráfico (figura 18.37) com os intervalos de confianças para a comparação de médias de frequência cardíaca para cada par de instantes de tempo.
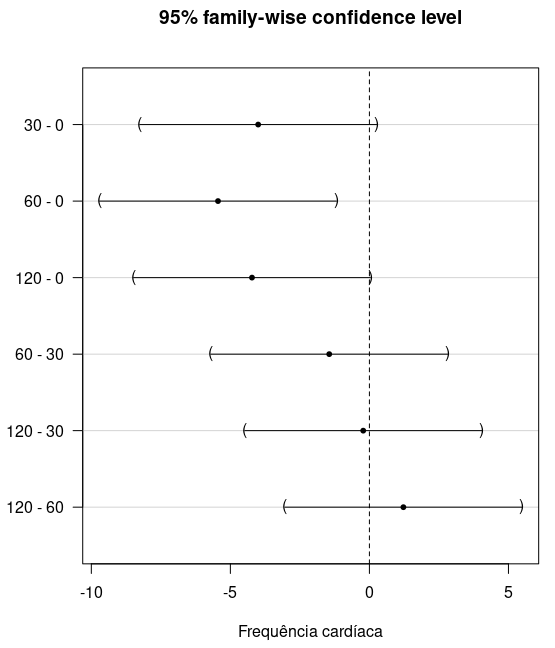
Figura 18.37: Diagrama que mostra os intervalos de confiança para a comparação de médias de frequência cardíaca para cada par de instantes de tempo, usando o método de Tukey.
Nesse exemplo, a diferença entre as medidas nos instantes 60 e 0 são estatisticamente significativas ao nível de 5%, e o intervalo de confiança ao nível de 95% dessa diferença indica uma redução máxima na média da frequência cardíaca entre esses dois instantes de 9,7 bpm.
18.4.6.1 Diagnósticos da ANOVA com medidas repetidas no R
Os conteúdos desta subseção e das subseções seguintes (18.4.6.1.1 a 18.4.6.1.4 e 18.4.6.2) podem ser visualizados neste vídeo.
Nesta seção, vamos avaliar os resíduos do modelo de ANOVA com medidas repetidas, gerado na seção anterior. Recordando, os resíduos para esse modelo são obtidos por meio da expressão
\(r_{ij} = X_{ij} - {\bar{X}}_{i.}- {\bar{X}}_{.j} + \bar{X}\)
onde:
\(X_{ij}\) é a medida da frequência cardíaca no instante j para o indivíduo i;
\({\bar{X}}_{i.}\) é a média da frequência cardíaca para o indivíduo i;
\({\bar{X}}_{.j}\) é a média da frequência cardíaca para o instante j;
\(\bar{X}\) é a média geral da frequência cardíaca para todos os indivíduos e todos os instantes de medida.
A sequência de comandos a seguir pode ser executada para gerar os resíduos para a frequência cardíaca e a figura 18.38 pode facilitar a compreensão desse processo:
heart.rate$media.hr.subj = ave(heart.rate$hr, heart.rate$subj)
heart.rate$media.hr.time = ave(heart.rate$hr, heart.rate$time)
heart.rate$media.geral = ave(heart.rate$hr)
heart.rate$residuos = heart.rate$hr - heart.rate$media.hr.subj -
heart.rate$media.hr.time + heart.rate$media.geralÀ esquerda, a figura 18.38 mostra o conjunto de dados heart.rateWide com as médias da frequência cardíaca em cada instante de medida, as médias da frequência cardíaca para cada indivíduo (médias das linhas) e a média geral da frequência cardíaca. À direita, a figura mostra o conjunto de dados heart.rate com o acréscimento das variáveis criadas na sequência de comandos acima.
O primeiro comando cria a variável media.hr.subj no conjunto de dados heart.rate que irá conter, para cada linha, a média da frequência cardíaca em todos os instantes para o indivíduo indicado na respectiva linha (variável subj). Essa média é obtida por meio da função ave que gera a média da variável indicada pelo primeiro argumento (hr) da função para cada nível da variável indicada pelo segundo argumento (subj). Todas as linhas para o mesmo indivíduo terão o mesmo valor de media.hr.subj.
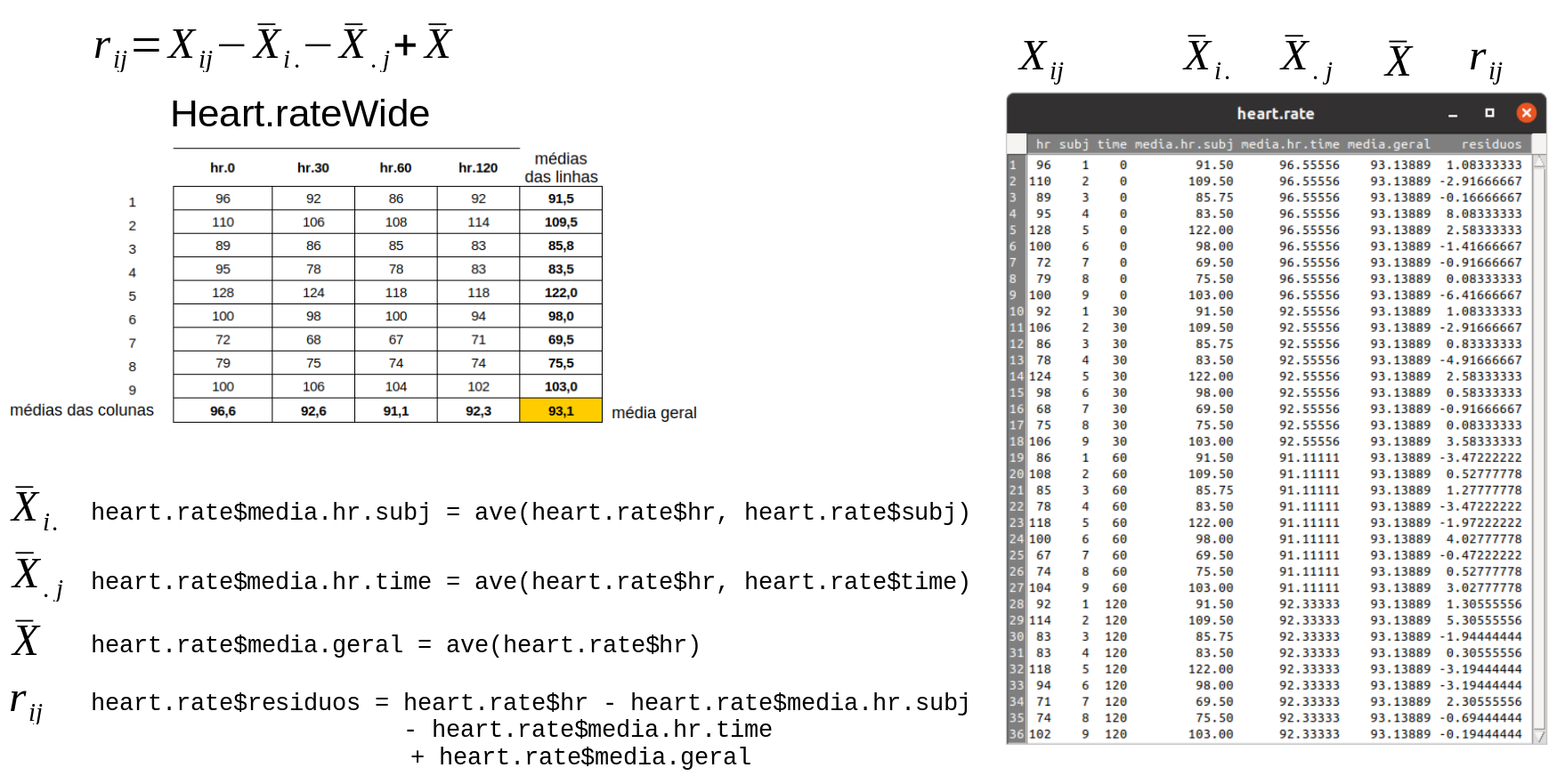
Figura 18.38: Figura que ilustra a geração dos resíduos para o modelo de ANOVA com medidas repetidas para o conjunto de dados heart.rate.
O segundo comando cria a variável media.hr.time no conjunto de dados heart.rate que irá conter, para cada linha, a média da frequência cardíaca de todos os indivíduos no instante indicado pelo valor da variável time na respectiva linha. Essa média também é obtida por meio da função ave, onde a variável de agrupamento, segundo argumento da função, é a variável time. Todas as linhas com o mesmo instante de medida terão o mesmo valor de media.hr.time.
O terceiro comando cria a variável media.geral no conjunto de dados heart.rate que irá conter em todas as linhas a média geral da frequência cardíaca de todos os indivíduos em todos os instantes. Essa média também é obtida por meio da função ave, sem especificação de variável de agrupamento.
Finalmente o quarto comando cria a variável residuos no conjunto de dados, aplicando a fórmula para os resíduos, utilizando as variáveis criadas nos comandos anteriores.
Com exceção da variávei residuos, não é necessário que as demais variáveis sejam acrescentadas ao conjunto de dados. Elas somente foram acrescentadas aqui para fins didáticos.
A partir dos resíduos, vamos nas seções seguintes gerar os seguintes diagramas:
um diagrama de comparação de quantis da normal dos resíduos;
um diagrama de pontos dos resíduos por instante de medida para avaliar a constância da variância do erro;
diagramas da sequência de resíduos por indivíduos para verificar a constância da variância do erro e interferência de outros fatores;
um diagrama de comparação de quantis dos efeitos principais devido aos indivíduos \(\bar{X_{i.}.}-\bar{X}\) pode ser útil para avaliar se os efeitos principais \(\rho_i\) estão normalmente distribuídos com variância constante.
18.4.6.1.1 Diagrama de comparação de quantis da normal para os resíduos
Uma vez obtido os resíduos para o conjunto de dados heart.rate, estando esse conjunto de dados como ativo no R Commander e supondo que o plugin RcmdrPlugin.EZR esteja carregado, para gerarmos o gráfico de comparação de quantis dos resíduos, acessamos a opção:
\[\text{Original menu} \Rightarrow\ \text{Gráficos} \Rightarrow \text{Gráfico de comparação de quantis...} \]
Na tela seguinte, selecionamos a variável residuos na lista de variáveis e clicamos em OK (figura 18.39).
Figura 18.39: Seleção da variável para a construção do gráfico de comparação de quantis da normal.
O comando executado é mostrado a seguir, seguido do diagrama (figura 18.40).
with(heart.rate, qqPlot(residuos, dist="norm", id=list(method="y", n=2,
labels=rownames(heart.rate))))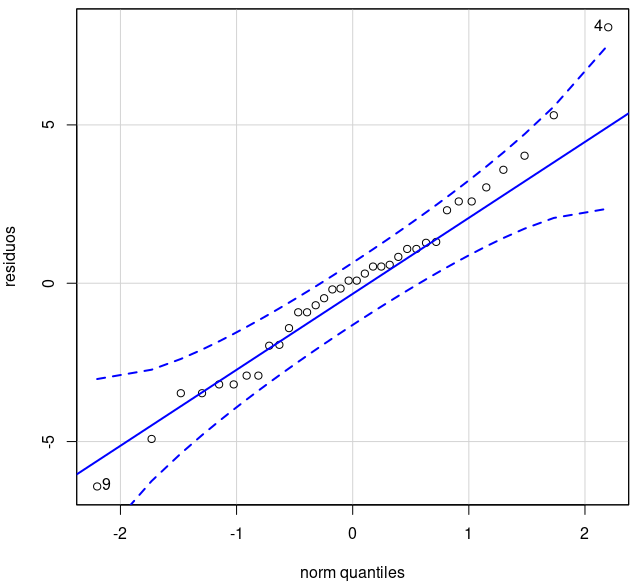
Figura 18.40: Gráfico de comparação de quantis da normal para os resíduos da frequência cardíaca.
Para realizarmos um teste de hipótese de normalidade dos resíduos, acessamos a opção:
\[\text{Original menu} \Rightarrow\ \text{Estatísticas} \Rightarrow\ \text{Resumos} \Rightarrow\ \text{Test of normality...}\]
Em seguida, selecionamos a variável que desejamos testar, o teste de normalidade a ser realizado (figura 18.41) e clicamos em OK.
Figura 18.41: Seleção da variável e do teste de normalidade que será realizado.
O resultado é mostrado a seguir. O teste não rejeita a hipótese de normalidade ao nível de 5% (p = 0,62), em concordância com a inspeção visual do gráfico de comparação de quantis da normal.
normalityTest(~residuals.AnovaModel.1, test="shapiro.test",
data=red.cell.folate)##
## Shapiro-Wilk normality test
##
## data: residuals.AnovaModel.1
## W = 0.966, p-value = 0.618818.4.6.1.2 Diagrama de pontos dos resíduos por instante de medida
Para gerarmos o diagrama de pontos dos resíduos por instante de medida, acessamos a opção:
\[\text{Original menu} \Rightarrow\ \text{Gráficos} \Rightarrow \text{Gráfico Strip chart} \]
Na tela seguinte, selecionamos a variável time como fator e a variável residuos na lista de variáveis resposta e clicamos em OK (figura 18.42).
Figura 18.42: Seleção da variável para a construção do gráfico de strip chart e da variável de agrupamento.
O comando executado é mostrado a seguir, seguido do diagrama (figura 18.43).
stripchart(residuos ~ time, vertical=TRUE, method="stack", ylab="residuos",
data=heart.rate)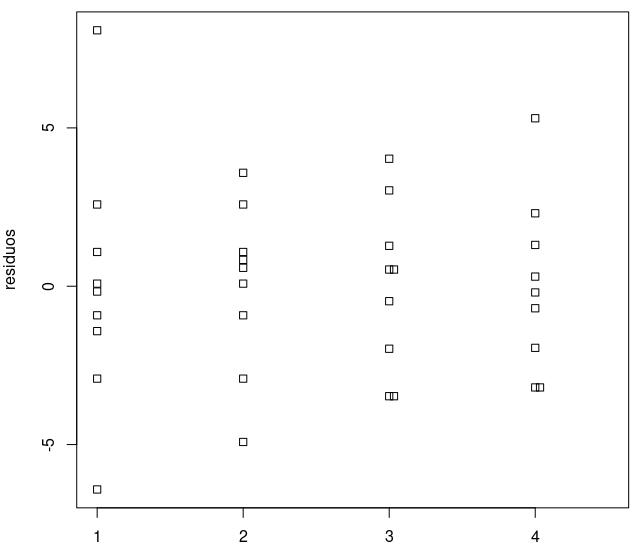
Figura 18.43: Gráfico de strip chart dos resíduos para cada instante de medida.
O diagrama de strip chart não sugere que haja diferenças das variâncias dos resíduos nos diferentes instantes de medida.
18.4.6.1.3 Diagramas da sequência dos resíduos por indivíduos
Os diagramas da sequência de resíduos por indivíduos podem ser úteis para verificar a constância da variância do erro e interferência de outros fatores. Eles são diagramas de dispersão dos resíduos x tempo, plotados separadamente para cada indivíduo. Para gerarmos esses diagramas no R Commander, precisamos que a variável time seja tratada como numérica. Para isso, o comando abaixo converte a variável time em inteira e cria a variável time.int no conjunto de dados heart.rate.
heart.rate$time.int = as.integer(heart.rate$time)Em seguida, para gerarmos os diagramas de sequência dos resíduos por indivíduos, acessamos a seguinte opção no menu:
\[\text{Original menu} \Rightarrow\ \text{Gráficos} \Rightarrow \text{Gráfico XY (dispersão) condicionado...} \]
Na tela seguinte (figura 18.44), selecionamos a variável time.int como variável explicativa, a variável residuos como variável resposta e a variável subj como condição.
Figura 18.44: Seleção das variáveis para a construção dos diagramas de dispersão dos resíduos x tempo para cada indivíduo.
Ao clicarmos em OK, o comando executado é mostrado a seguir, seguido do diagrama que mostra a dispersão dos resíduos x tempo de medida para cada indivíduo separadamente (figura 18.45).
xyplot(residuos ~ time | subj, type="p", pch=16, auto.key=list(border=TRUE),
par.settings=simpleTheme(pch=16), scales=list(x=list(relation='same'),
y=list(relation='same')), data=heart.rate)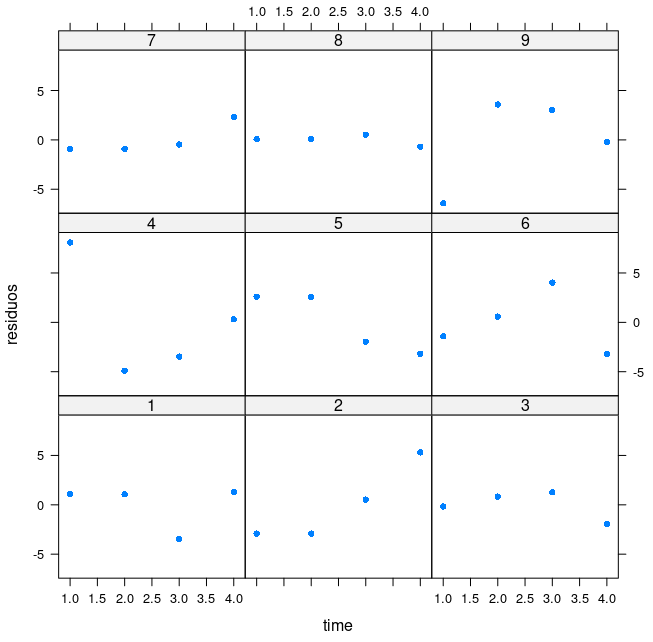
Figura 18.45: Diagrama que mostra a dispersão dos resíduos x tempo de medida para cada indivíduo separadamente.
Os diagramas não sugerem um padrão na distribuição dos resíduos em relação ao tempo, mas é preciso destacar que a amostra é pequena e há apenas 4 pontos por indivíduo.
18.4.6.1.4 diagrama de comparação de quantis dos efeitos principais devido aos indivíduos
Um diagrama de comparação de quantis dos efeitos principais devido às unidades de análise, \(\bar{X_{i.}.}-\bar{X}\), é utilizado para avaliar se os efeitos principais \(\rho_i\) estão normalmente distribuídos. Para construir esse diagrama, precisamos obter os desvios das médias de cada indivíduo em relação à média geral, que podem ser obtidos por meio do comando a seguir:
res.medias.subj = rowMeans(heart.rateWide) - mean(heart.rate$hr)Nesse comando, a função rowMeans calcula a média de cada linha do conjunto de dados heart.rateWide, fornecendo então a média da frequência cardíaca para cada indivíduo. Em seguida, essas médias são subtraídas da média geral da frequência cardíaca (mean(heart.rate$hr)), gerando então a variável desejada (res.medias.subj).
O comando a seguir gera o gráfico de comparação de quantis da normal para a variável res.medias.subj, exibido na figura 18.46.
qqPlot(res.medias.subj, dist="norm", xlab = "quantis da normal",
ylab = "média dos indivíduos - média geral")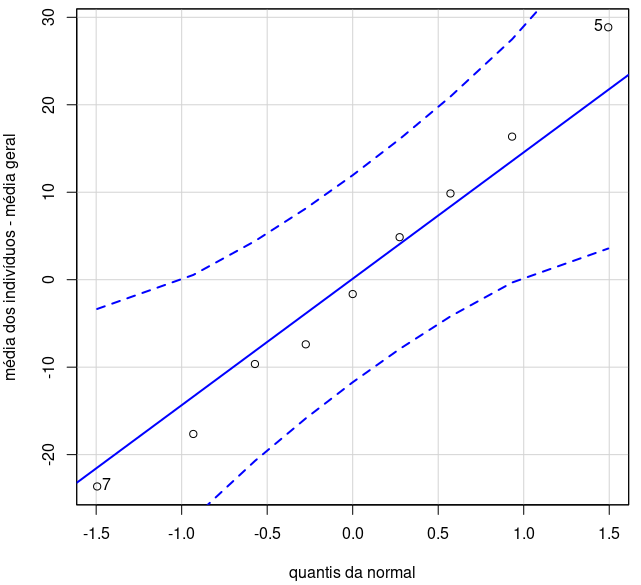
Figura 18.46: Gráfico de comparação dos quantis da normal dos desvios das médias dos indivíduos em relação à média geral.
O comando seguinte realiza o teste de Shapiro-Wilk para a variável res.medias.subj. O teste não rejeita a hipótese de normalidade ao nível de 5% (p = 0,98), em concordância com a inspeção visual do gráfico de comparação de quantis da normal.
normalityTest(~ res.medias.subj, test="shapiro.test")##
## Shapiro-Wilk normality test
##
## data: res.medias.subj
## W = 0.98376, p-value = 0.980818.4.6.2 Teste de Friedman no R
Para realizarmos o teste de Friedman, usando o plugin RcmdrPlugin.EZR, acessamos a opção:
\[\text{Statistical analysis} \Rightarrow \text{Testes não paramétricos} \Rightarrow \text{Friedman test}\]
Na tela seguinte, selecionamos as variáveis que indicam as medidas repetidas e selecionamos o método, ou métodos, que serão utilizados para realizar um teste para a comparação par a par das distribuições das medidas de frequência cardíaca em cada instante (figura 18.47).
Figura 18.47: Seleção das variáveis que serão analisadas pelo teste de Friedman.
Os comandos executados são mostrados a seguir, seguido dos resultados.
Inicialmente, são mostradas as medianas da frequência cardíaca para cada instante de medida. O teste de Friedman rejeitou a hipótese nula de igualdade das distribuições das medidas de frequência cardíaca em cada instante, mas não teve poder estatístico para apontar diferenças entre os pares de distribuições. Nenhum valor de p para as comparações par a par foram abaixo de 5%. Não são mostradas aqui as mensagens geradas pelo R de que a presença de empates ou zeros não permite o cálculo de valores de p exatos.
#####Friedman test#####
.Responses <- na.omit(with(heart.rateWide,
cbind(hr.0, hr.30, hr.60, hr.120)))
apply(.Responses, 2, median)## hr.0 hr.30 hr.60 hr.120
## 96 92 86 92res <- NULL
(res <- friedman.test(.Responses))##
## Friedman rank sum test
##
## data: .Responses
## Friedman chi-squared = 8.5059, df = 3, p-value = 0.03664cat(gettext(domain="R-RcmdrPlugin.EZR", "Friedman test"), " ",
gettext(domain="R-RcmdrPlugin.EZR", "p.value"), " = ",
signif(res$p.value, digits=3), "", sep="")## Friedman test p.value = 0.0366pairwise.friedman.test(.Responses, "heart.rateWide", p.adjust.method="holm")##
## Pairwise comparisons using Wilcoxon signed rank test
##
## data: heart.rateWide
##
## hr.0 hr.30 hr.60
## hr.30 0.37 - -
## hr.60 0.21 0.86 -
## hr.120 0.25 0.89 0.89
##
## P value adjustment method: holm18.5 Outros tipos de análise de variância
Nas seções anteriores, foram apresentadas duas situações em que a análise de variância pode ser aplicada. A análise de variância pode, entretanto, ser utilizada em diversos outros contextos, por exemplo, com dois ou mais fatores ou variáveis independentes, com ou sem medidas repetidas. No caso de medidas repetidas, o modelo apresentado na seção 18.4 considerava que cada paciente possuía uma e somente uma medida em cada instante ou em cada nível do fator em estudo; entretanto outras situações podem ocorrer como, por exemplo, um paciente não possuir todas as medidas ou possuir mais de uma medida em um determinado nível do fator. Outras formas de amostragem também podem ser utilizadas na análise de variância. Kutner et al. (Kutner et al. 2005) apresentam um visão bem ampla das diversas situações em que a análise de variância pode ser aplicada.
18.6 Exercícios
Com o conjunto de dados birthwt do pacote MASS (GPL-2 | GPL-3), faça as atividades abaixo.
- Veja a ajuda para esse conjunto de dados.
- Compare as médias da variável bwt (peso ao nascer) entre os três grupos de raças das mães. Obtenha o intervalo de confiança ao nível de 95% para a diferença das médias entre os três grupos, usando o método de Tukey.
- Verifique as suposições para a realização da ANOVA para um fator.
- Realize o teste de Kruskal-Wallis para a comparação do peso ao nascer entre os três grupos de raças das mães.
O conjunto de dados WeightLoss do pacote carData (GPL-2 | GPL-3) contém dados artificiais sobre perda de peso e auto-estima ao longo de três meses, para três grupos de indivíduos: Controle, Dieta e Dieta + Exercício.
- Crie um subconjunto de dados de WeightLoss, chamado wlDietEx, com dados somente dos indivíduos que fizeram dieta + exercício, por meio do comando ao final do exercício 2 do capítulo anterior (capítulo 16).
- Com o conjunto de dados wlDietEx, compare as médias de perdas de peso nos três meses. Utilize o nível de significância igual a 5%.
- Faça o gráfico de interação entre as unidades de análise (pacientes) e o tempo de medição e comente o resultado.
- Adapte o script da seção 18.4.6 para obter o intervalo de confiança ao nível de 85% para as diferenças de perda de peso entre as três medições. Comente os resultados.
- Transforme o conjunto de dados wlDietEx para o formato longo, usando o primeiro comando ao final do exercício, gerando o conjunto de dados wlDietExLong. Para uma compreensão de como essa transformação é realizada, veja este vídeo.
- Use o segundo comando ao final do exercício para calcular os resíduos do modelo, faça o gráfico de comparação de quantis da normal para os resíduos e faça um teste de normalidade dos resíduos. Comente os resultados.
- Faça o diagrama de pontos dos resíduos por instantes de medida. Comente o gráfico.
- Converta a variável mes de wlDietEx para inteiro e faça o diagrama da sequência dos resíduos por indivíduos. Comente os gráficos.
- Use a terceira sequência de comandos ao final do exercício para verificar a normalidade dos efeitos principais devido aos indivíduos. Comente os resultados.
- Faça o teste de Friedman e comente os resultados.
Convertendo wlDietEx para o formato longo:
wlDietExLong <- reshapeW2L(wlDietEx, within="mes",
levels=list(mes=c("1", "2", "3")),
varying=list(wl=c("wl1", "wl2", "wl3")), id="id")Calculando os residuos para o modelo:
wlDietExLong$residuos = wlDietExLong$wl -
ave(wlDietExLong$wl, wlDietExLong$id) -
ave(wlDietExLong$wl, wlDietExLong$mes) +
ave(wlDietExLong$wl)Verificando a normalidade dos efeitos principais devido aos indivíduos:
res.medias.subj = rowMeans(wlDietEx) - mean(wlDietExLong$wl)
qqPlot(res.medias.subj, dist="norm", xlab = "quantis da normal",
ylab = "média dos indivíduos - média geral")
normalityTest(~ res.medias.subj, test="shapiro.test")