17 Comparação de proporções

17.1 Introdução

O conteúdo desta seção pode ser visualizado neste vídeo.

Os métodos apresentados sobre comparação de médias de uma variável numérica entre duas amostras são aplicáveis quando se compara a média de uma variável contínua em duas amostras independentes ou dependentes.

Em muitos estudos, estamos interessados em relações entre variáveis categóricas nominais ou ordinais.

No capítulo 8 (Medidas de associação), foram apresentadas diferentes medidas de associação entre variáveis dicotômicas a partir de uma tabela 2x2 (tabela 17.1).

Tabela 17.1: Tabela 2x2 que verifica a associação entre duas variáveis dicotômicas.

	Desfecho Clínico
Exposição	Sim	Não	Total
Nível 1	n11	n12	n1+ = n11 + n12
Nivel 2	n21	n22	n2+ = n21 + n22
Total	n+1 = n11 + n21	n+2 = n12 + n22	n = n1+ + n2+

O risco de um indivíduo apresentar o desfecho clínico de interesse quando está exposto ao nível 1 de um fator é dado por:

\[\begin{align} R_{N1} = \frac{n_{11}}{n_{1+}} \tag{17.1} \end{align}\]

A expressão (17.1) é uma estimativa da probabilidade de um indivíduo apresentar o desfecho clínico de interesse ao estar exposto ao nível 1 do fator.

Analogamente, o risco de um indivíduo apresentar o desfecho clínico de interesse quando está exposto ao nível 2 de um fator é dado por:

\[\begin{align} R_{N2} = \frac{n_{21}}{n_{2+}} \tag{17.2} \end{align}\]

A expressão (17.2) é uma estimativa da probabilidade de um indivíduo apresentar o desfecho clínico de interesse ao estar exposto ao nível 2 do fator.

Neste capítulo, vamos chamar R_N1 e R_N2 de p₁ e p₂, respectivamente.

\(\ \ p_1 = R_{N1}\), \(\ \ p_2 = R_{N2}\)

Ao realizarmos um estudo e observarmos uma tabela 2x2 como a tabela 17.1, estamos interessados em responder às seguintes questões:

1. obter medidas de associação (diferença absoluta de riscos - DAR, risco relativo - RR, razão de chances - RC, etc.) para o estudo e testar a hipótese de que não haja associação entre as duas variáveis;

2. obter os intervalos de confiança das medidas de associação.

Recordando:

\(\begin{aligned} &\ DAR = p_1 - p_2 \end{aligned}\)

\(\begin{aligned} &\ RR = \frac{p_1}{p_2} \end{aligned}\)

\(\begin{aligned} &\ RC = \frac{\frac{p_1}{1-p_1}}{\frac{p_2}{1-p_2}} \end{aligned}\)

Neste capítulo, vamos responder a essas perguntas, considerando as três medidas de associação listadas acima a partir de duas situações distintas:

1. quando as amostras de indivíduos expostos aos diferentes níveis do fator em estudo são independentes;

2. quando as amostras de indivíduos expostos aos diferentes níveis do fator em estudo são dependentes (ou pareadas).

Testar a hipótese de que não hava associação entre a variável de exposição e o desfecho é equivalente a testar que o fator de exposição não tem influência sobre o desfecho, ou seja, que as variáveis fator de exposição e desfecho clínico são independentes, ou de maneira equivalente:

DAR = 0, ou RR = RC = 1.

As três igualdades acima implicam que as proporções p₁ e p₂ são iguais.

Também vamos realizar um teste de independência das variáveis quando as variáveis de exposição ou de desfecho possuem mais de duas categorias.

O estudo de Hjerkind, Stenehjem e Nilsen (Hjerkind, Stenehjem, and Nilsen 2017) é um exemplo de um estudo com amostras independentes. Trata-se de um estudo prospectivo que verifica a associação entre as variáveis categóricas adiposidade e atividade física e diabetes mellitus. A figura 17.1 mostra a tabela 3 desse estudo. Essa tabela mostra os resultados, expressos como risco relativo, do acompanhamento de 38.413 pessoas estratificadas em diversos grupos, ou níveis de atividade física, e por sexo.

Os estratos ou grupos são independentes, porque os grupos foram formados naturalmente a partir do nível de atividade física de cada pessoa que participou do estudo. Não houve, por exemplo, nenhum pareamento entre indivíduos de um estrato com outro por sexo, idade ou outra variável.

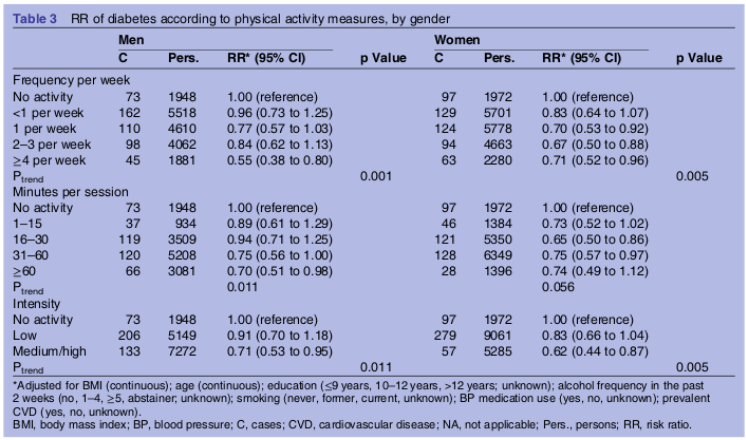
Figura 17.1: Exemplo de um estudo com amostras independentes. Tabela 3 do estudo de (Hjerkind, Stenehjem, and Nilsen 2017) (CC BY-NC).

Para testar hipóteses e calcular intervalos de confiança para parâmetros populacionais, quando as observações nas amostras são independentes e as variáveis de exposição e desfecho são variáveis categóricas, a análise mais simples envolve a utilização do teste qui ao quadrado para amostras independentes quando as amostras são suficientemente grandes. Quando as amostras são pequenas, utiliza-se o chamado teste exato de Fisher-Erwin.

O estudo de Severo et al. (Severo et al. 2018) é um exemplo de um estudo com amostras dependentes. A figura 17.2 mostra parte da tabela 1 desse estudo, que mostra a associação entre fatores de risco e quedas em pacientes adultos hospitalizados. Por exemplo, entre os casos de queda 81% tinham limitação para caminhar contra 67% no grupo controle (não tiveram queda).

Apesar de a apresentação da tabela ser semelhante ao exemplo anterior, esse estudo é um estudo de caso-controle, onde cada caso foi pareado com um controle em relação ao sexo, à unidade e data da internação, ou seja, para cada caso de queda durante a hospitalização, foi identificado um controle (que não teve queda) que fosse do mesmo sexo e com a mesma data e unidade de internação. Dizemos que, neste caso, as amostras são dependentes e veremos que a análise é diferente da análise para o caso de amostras dependentes.

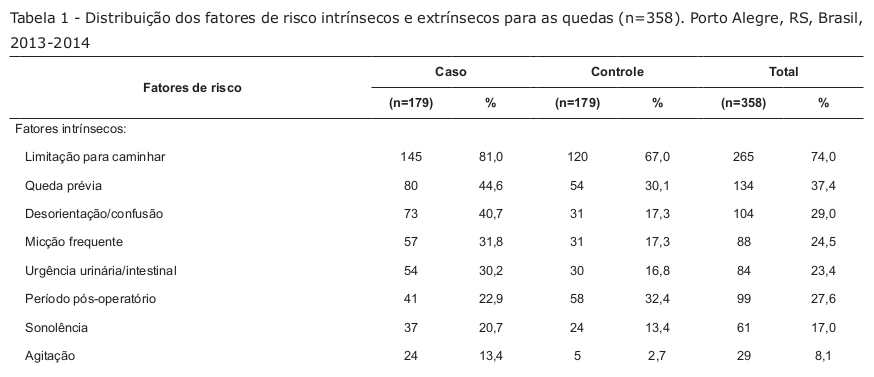
Figura 17.2: Exemplo de um estudo de caso-controle com amostras dependentes (estudo pareado). Parte da tabela 1 do estudo de (Severo et al. 2018) (CC BY).

Em um estudo com amostras dependentes, as observações nas 2 amostras são relacionadas, seja porque dois tratamentos distintos são aplicados em sequência a um conjunto de pacientes (a ordem de aplicação pode ser aleatória) e, então, uma variável de desfecho categórica é medida após cada tratamento, seja porque um controle é pareado com um caso em um estudo de caso-controle, sendo que cada par é formado por indivíduos semelhantes de acordo com um critério estabelecido, como no estudo de Severo et al. (Severo et al. 2018).

Uma análise simples, frequentemente utilizada nesses casos, é o teste de McNemar.

Na próxima seção, vamos ver como são realizados os testes qui ao quadrado e o teste exato de Fisher-Erwin para tabelas 2x2 com amostras independentes e como são calculados o intervalo de confiança para as medidas de associação DAR, RR e RC para amostras suficientemente grandes.

17.2 Comparação de proporções em duas amostras independentes

Nesta seção, serão abordados dois testes estatísticos para verificar a associação entre duas variáveis categóricas: o teste qui ao quadrado e o teste exato de Fisher. Também serão apresentados os intervalos de confiança aproximados, quando as amostras não são pequenas, para as medidas de associação: diferença de risco, risco relativo e razão de chances. Nesta seção, consideraremos que as duas amostras, correspondentes aos níveis 1 e 2 do fator de exposição, foram obtidas de maneira independente.

17.2.1 Teste qui ao quadrado

Os conteúdos desta seção e das seções 17.2.2 a 17.2.5 podem ser visualizados neste vídeo.

O teste qui ao quadrado é utilizado para verificar se a associação entre duas variáveis dicotômicas é estatisticamente significativa, quando as amostras são suficientemente grandes.

A partir da tabela 17.1, podemos derivar a tabela 17.2, dividindo-se cada célula da tabela 17.1 por n, o tamanho total das duas amostras, obtendo-se então as proporções observadas em cada célula:

\(\ p_{11} = \frac{n_{11}}{n}\), \(p_{12} = \frac{n_{12}}{n}\), \(p_{21} = \frac{n_{21}}{n}\), \(p_{22} = \frac{n_{22}}{n}\)

\(\ p_{1+} = \frac{n_{1+}}{n}= p_{11} + p_{12}\),  \(p_{+1} = \frac{n_{+1}}{n}= p_{11} + p_{21}\)

\(\ p_{2+} = \frac{n_{2+}}{n}= p_{21} + p_{22}\),  \(p_{+2} = \frac{n_{+2}}{n}= p_{12} + p_{22}\)

Tabela 17.2: Tabela 2x2 que verifica a associação entre duas variáveis dicotômicas, obtida da tabela 17.1, dividindo-se cada célula por n.

	Desfecho Clínico
Exposição	Sim	Não	Total
Nível 1	p11	p12	p1+ = p11 + p12
Nivel 2	p21	p22	p2+ = p21 + p22
Total	p+1 = p11 + p21	p+2 = p12 + p22	1

Sob a hipótese de independência das variáveis Exposição e Desfecho Clínico, as proporções esperadas de indivíduos em cada célula da tabela seriam:

\(\begin{aligned} &\ p_{11} = P[(\text{Exposição = Nível 1})\ \cap\ (\text{Desfecho Clínico = Sim})]=p_{1+}\ p_{+1} \end{aligned}\)

\(\begin{aligned} &\ p_{21} = P[(\text{Exposição = Nível 2})\ \cap\ (\text{Desfecho Clínico = Sim})]=p_{2+}\ p_{+1} \end{aligned}\)

\(\begin{aligned} &\ p_{12} = P[(\text{Exposição = Nível 1})\ \cap\ (\text{Desfecho Clínico = Não})]=p_{1+}\ p_{+2} \end{aligned}\)

\(\begin{aligned} &\ p_{22} = P[(\text{Exposição = Nível 2})\ \cap\ (\text{Desfecho Clínico = Não})]=p_{2+}\ p_{+2} \end{aligned}\)

A frequência esperada na célula correspondente ao nível 1 da exposição e o valor Sim para o desfecho clínico seria dada por:

\(\begin{aligned} &\ E_{11} = n\ p_{1+}\ p_{+1} = n\frac{n_{1+}}{n}\frac{n_{+1}}{n}= \frac{n_{1+}\ n_{+1}}{n} \end{aligned}\)

De modo análogo, são obtidas as frequências esperadas para as demais células (tabela 17.3).

Tabela 17.3: Valores esperados em cada célula da tabela 17.1, sob a hipótese de independência das variáveis.

	Desfecho Clínico
Exposição	Sim	Não	Total
Nível 1	E11 = (n1+ n+1)/n	E12 = (n1+ n+2)/n	n1+
Nivel 2	E21 = (n2+ n+1)/n	E22 = (n2+ n+2)/n	n2+
Total	n+1	n+2	n

Sob a hipótese nula (independência dos eventos), espera-se que as frequências observadas (\(O_{ij}\)) em cada célula não sejam muito diferentes das frequências esperadas. A estatística abaixo:

\[\begin{align} \chi^2 = \sum_{i=1}^{2}\sum_{j=1}^{2}\frac{(O_{ij}-E_{ij})^2}{E_{ij}} \tag{17.3} \end{align}\]

segue aproximadamente uma distribuição qui ao quadrado, com 1 grau de liberdade, quando a hipótese nula é verdadeira. Assim valores suficientemente altos de \(\chi^2\) levam à rejeição da hipótese nula. Esse teste foi proposto pelo estatístico Karl Pearson (K. Pearson 1900).

Vamos voltar à tabela 8.2 do capítulo 8, derivada do estudo de Hjerkind, Stenehjem e Nilsen (Hjerkind, Stenehjem, and Nilsen 2017) e mostrada novamente na tabela 17.4.

Tabela 17.4: Versão simplificada da tabela 3 do estudo de Hjerkind, Stenehjem e Nilsen (Hjerkind, Stenehjem, and Nilsen 2017) (CC BY-NC). Essa tabela mostra somente dois níveis de atividade física.

	Diabetes Mellitus
Atividade Física	Sim	Não	Total
Exercita 4+ vezes/semana	45	1836	1881
Inativo	73	1875	1948
Total	118	3711	3829

Vamos realizar o teste qui ao quadrado para esse exemplo. A tabela 17.5 mostra as frequências esperadas para as células, caso a atividade física não tenha influência sobre a ocorrência de diabetes mellitus.

Tabela 17.5: Valores esperados nas células da tabela 17.4 sob a hipótese de independência das variáveis.

	Diabetes Mellitus
Atividade Física	Sim	Não	Total
Inativo	58	1823	1881
Exercita 4+ vezes/semana	60	1888	1948
Total	118	3711	3829

Então:

\(\begin{aligned} &\ \chi^2 = \frac{(45-58)^2}{58} + \frac{(73-60)^2}{60} + \frac{(1836-1823)^2}{1823} + \frac{(1875-1888)^2}{1888} = 5,91 \end{aligned}\)

Usando o R, podemos obter a probabilidade de se obter um valor tão ou mais elevado do que 5,91 na distribuição qui ao quadrado com 1 grau de liberdade:

pchisq(5.91, 1, lower.tail = FALSE)

## [1] 0.01505517

O valor de p é igual a 0,015. Se o nível de significância do teste fosse de 5%, nós rejeitaríamos a hipótese nula de igualdade de riscos.

17.2.2 Intervalos de confiança para a DAR, o RR e a RC

Diferença de riscos

Para amostras suficientemente grandes, o erro padrão (ep) e o intervalo de confiança (IC) para a diferença de riscos (DAR) podem ser aproximados por (Fleiss 1981):

\(\ DAR = p_1 - p_2, \ \ \ \ ep(DAR) = \sqrt{ \frac{p_1(1-p_1)}{n_{1+}} + \frac{p_2(1-p_2)}{n_{2+}}}\)

\(\ IC(DAR):\ (p_1 - p_2) \pm z_{\alpha/2}\ \sqrt{ \frac{p_1(1-p_1)}{n_{1+}} + \frac{p_2(1-p_2)}{n_{2+}}}\)

Para os dados da tabela 17.4 e para um IC com 95% de confiança, temos:

\(p_1 = \frac{45}{1881} = 0,0239\), \(\ p_2 = \frac{73}{1948} = 0,0375\)

\(\ IC(DAR): (0,0239 - 0,0375) \pm 1,96\ \sqrt{\frac{0,0239\ .\ 0,9761}{1881} + \frac{0,0375\ .\ 0,9625}{1948}}\)

IC(DAR) = [-0,0246; -0,0026] = [-2,46%; -0,26%]

Risco relativo

Para amostras suficientemente grandes, o erro padrão (ep) e o intervalo de confiança (IC) para o logaritmo neperiano do risco relativo (RR) podem ser aproximados por (Rothman, Greenland, and Lash 2011):

\(\ RR = \frac{p_1}{p_2}, \ \ \ \ ep[ln(RR)] = \sqrt{\frac{1}{n_{11}} + \frac{1}{n_{1+}} + \frac{1}{n_{21}} + \frac{1}{n_{2+}}}\)

\(\ \ IC[ln(RR)]:\ ln(RR) \pm z_{\alpha/2} \ \sqrt{\frac{1}{n_{11}} + \frac{1}{n_{1+}} + \frac{1}{n_{21}} + \frac{1}{n_{2+}}}\)

Para os dados da tabela 17.4 e para um IC com 95% de confiança, temos:

\(\ RR = \frac{0,0239}{0,0375} = 0,64\)

\(\ \ IC[ln(RR)]:\) \(ln(0,64) \pm 1,96\ \sqrt{ \frac{1}{45} + \frac{1}{1881} + \frac{1}{73} + \frac{1}{1948}} = -0,45\pm 0,366\)

IC[ln(RR)] = [-0,81; -0,08]

Para obtermos o intervalo de confiança para o risco relativo, precisamos elevar a base “e” aos limites do intervalo de confiança de ln(RR):

\(\ IC(RR) = [e^{-0,81} - e^{-0,08}] = [0,44 - 0,92]\)

Razão de chances

Para amostras suficientemente grandes, o erro padrão (ep) e o intervalo de confiança (IC) para o logaritmo neperiano da razão de chances (RR) podem ser aproximados por (Fleiss 1981):

\(\ RC = \frac{\frac{p_1}{1-p_1}}{\frac{p_2}{1-p_2}}, \ \ \ \ ep[ln(RC)] = \sqrt{\frac{1}{n_{11}} + \frac{1}{n_{12}} + \frac{1}{n_{21}} + \frac{1}{n_{22}}}\)

\(\ \ IC[ln(RC)]:\) \(ln(RC) \pm z_{\alpha/2} \ \sqrt{\frac{1}{n_{11}} + \frac{1}{n_{12}} + \frac{1}{n_{21}} + \frac{1}{n_{22}}}\)

Para os dados da tabela 17.4 e para um IC com 95% de confiança, temos:

\(\ RC = \frac{\frac{0,0239}{1-0,0239}}{\frac{0,0375}{1-0,0375}} = \frac{0,03896}{0,02449} = 0,63\)

\(\ \ IC[ln(RC)]:\) \(ln(0,63) \pm 1,96\ \sqrt{\frac{1}{45} + \frac{1}{1836} + \frac{1}{73} + \frac{1}{1875}} = -0,462\pm 0,377\)

IC[ln(RC)] = [-0,84; -0,085]

Para obtermos o intervalo de confiança para a razão de chances, precisamos elevar a base “e” aos limites do intervalo de confiança de ln(RC):

\(\ IC(RC) = [e^{-0,84} - e^{-0,085}] = [0,43 - 0,92]\)

17.2.3 Usando o epiR para o teste do qui ao quadrado e cálculo das medidas de associação

Recordando o capítulo 8, seção 8.3, podemos realizar as análises das duas seções anteriores por meio do epiR, utilizando os seguintes comandos:

library(epiR)
table <- matrix(c(45, 1836, 73, 1875), 2, 2, byrow=TRUE)
epi.2by2(table, method = "cohort.count", conf.level = 0.95)

##              Outcome +    Outcome -      Total        Inc risk *        Odds
## Exposed +           45         1836       1881              2.39      0.0245
## Exposed -           73         1875       1948              3.75      0.0389
## Total              118         3711       3829              3.08      0.0318
## 
## Point estimates and 95 % CIs:
## -------------------------------------------------------------------
## Inc risk ratio                               0.64 (0.44, 0.92)
## Odds ratio                                   0.63 (0.43, 0.92)
## Attrib risk *                                -1.36 (-2.45, -0.27)
## Attrib risk in population *                  -0.67 (-1.67, 0.34)
## Attrib fraction in exposed (%)               -56.64 (-125.88, -8.63)
## Attrib fraction in population (%)            -21.60 (-39.84, -5.74)
## -------------------------------------------------------------------
##  X2 test statistic: 5.883 p-value: 0.015
##  Wald confidence limits
##  * Outcomes per 100 population units

Nos resultados mostrados, o risco relativo é identificado por Inc risk ratio, e a diferença de riscos é denominada Attrib risk. Observem que os intervalos de confiança são próximos aos calculados pelas fórmulas apresentadas.

A seção 8.3 do capítulo sobre medidas de associação mostra como analisar uma tabela 2x2 para amostras independentes a partir de um conjunto de dados, tanto no R Commander quanto usando o pacote epiR.

17.2.4 Alternativas ao teste qui ao quadrado tradicional

A estatística apresentada pela expressão (17.3) é a mais usada para realizar um teste de hipótese em tabelas 2 x 2. Porém outras alternativas foram propostas. Pode-se mostrar que a estatística (17.3) pode também ser expressa como:

\[\begin{align} \chi^2 = \frac{n(n_{11}n_{22}-n_{12}n_{21})^2}{n_{+1}n_{+2}n_{1+}n_{2+}} \tag{17.4} \end{align}\]

onde n é a soma das frequências na tabela 17.1.

Egon Pearson (E. Pearson 1947) propôs a substituição de n em (17.4) por (n – 1):

\[\begin{align} \chi_{EP}^2 = \frac{(n-1)(n_{11}n_{22}-n_{12}n_{21})^2}{n_{+1}n_{+2}n_{1+}n_{2+}}=\frac{n-1}{n}\chi^2 \tag{17.5} \end{align}\]

À medida que n aumenta, a razão (n-1)/n se aproxima de 1 e a expressão (17.5) se aproxima da expressão (17.4).

Yates (Yates 1934) propôs uma outra alternativa, que ele chamou de correção de continuidade, que está disponível em diversos softwares estatísticos:

\[\begin{align} \chi_{Y}^2 = \frac{n(|n_{11}n_{22}-n_{12}n_{21}|-\frac{n}{2})^2}{n_{+1}n_{+2}n_{1+}n_{2+}} \tag{17.6} \end{align}\]

Quão grande devem ser as amostras para que as análises apresentadas nas duas seções anteriores sejam válidas?

Essa é uma questão que tem suscitado longos debates. Campbell (Campbell 2007) realizou uma comparação de diversas propostas e chegou à conclusão que a melhor política para a análise de tabelas 2x2 para estudos de coortes, ensaios randomizados ou estudos transversais é a seguinte:

1. quando todos os valores esperados nas células são maiores ou iguais a 1, utilize a proposta de Egon Pearson (expressão (17.5)) que é o qui ao quadrado tradicional com n substituído por n-1;

2. para os demais casos, use o teste exato de Fisher–Irwin, com o teste bilateral realizado de acordo com a regra de Irwin (como mostrado na seção 17.2.5).

O R Commander não oferece uma opção para realizar o teste qui ao quadrado de acordo com a proposta de Egon Pearson. Entretanto pode-se obter o resultado do teste qui ao quadrado do R Commander e modificá-lo para implementar o teste de Egon Pearson (E. Pearson 1947).

Vamos repetir o teste qui ao quadrado da seção 8.3 do capítulo 8 (figuras 8.2 a 8.4). Os comandos a seguir foram executados para montar a tabela 2 x 2 e realizar o teste qui ao quadrado para as variáveis diab (diabético) e dead (óbito) do conjunto de dados stroke do pacote ISwR (GPL-2 | GPL-3).

data(stroke, package="ISwR")
local({
  .Table <- xtabs(~diab+dead, data=stroke)
  cat("\nFrequency table:\n")
  print(.Table)
  .Test <- chisq.test(.Table, correct=FALSE)
  print(.Test)
})

## 
## Frequency table:
##      dead
## diab  FALSE TRUE
##   No    308  414
##   Yes    35   62
## 
##  Pearson's Chi-squared test
## 
## data:  .Table
## X-squared = 1.5196, df = 1, p-value = 0.2177

A tabela 2 x 2 gerada (.Table) nesse teste pode ser utilizada para, então, substituir n por n-1 na expressão (17.4) e realizar o teste qui ao quadrado segundo Egon Pearson. A sequência de comandos abaixo realiza este procedimento:

.Table <- xtabs(~diab+dead, data=stroke)
n <- sum(.Table)
r <- as.numeric(chisq.test(.Table, correct = FALSE)$statistic)
pchisq(r*(n-1)/n, 1, lower.tail = FALSE)

## [1] 0.2179651

O primeiro comando recria a tabela 2 x 2, que é armazenada no objeto .Table. O comando seguinte obtém a frequência total da tabela (soma de todas as células). O terceiro comando recupera a estatística do teste qui ao quadrado tradicional, expressão (17.4). O último comando substitui n por n-1 no cálculo da expressão (17.4) para a tabela 2 x 2 e calcula o valor de p. O resultado é 0,218, bastante próximo ao do teste qui ao quadrado tradicional, já que o valor de n (819) é muito próximo de n – 1.

17.2.5 Teste exato de Fisher-Irwin

Para tabelas 2x2 com valores esperados muito pequenos nas células, uma alternativa bastante utilizada é o chamado teste exato de Fisher (ou teste exato de Fisher-Irwin). Esse método consiste em calcular as probabilidades associadas a todas as tabelas possíveis que possuem os mesmos totais nas linhas e colunas que os valores observados na tabela, com a suposição de que a hipótese nula é verdadeira, ou seja, que as variáveis representadas nas linhas e colunas são independentes.

Considerando a tabela 17.6, supondo que a variável de exposição não seja relacionada ao desfecho e que os totais nas linhas e colunas (n₊₁, n₊₂, n₁₊, n₂₊) sejam fixos, então a frequência da célula correspondente ao nível 1 da variável exposição e ao nível Sim da variável desfecho é uma variável aleatória que segue uma distribuição conhecida por distribuição hipergeométrica.

Tabela 17.6: Tabela 2x2, fixando os totais nas linhas e colunas.

	Desfecho Clínico
Exposição	Sim	Não	Total
Nível 1	n11	n12	n1+
Nivel 2	n21	n22	n2+
Total	n+1	n+2	n = n1+ + n2+

Pode-se mostrar nesse caso que a probabilidade de se observar a frequência n₁₁ é dada por:

\[\begin{align} P(n_{11})= \frac{\binom{n_{1+}}{n_{11}} \binom{n_{2+}}{n_{+1}-n_{11}}}{\binom{n}{n_{+1}}} = \frac{n_{1+}!n_{+1}!n_{2+}!n_{+2}!}{n! n_{11}!n_{12}!n_{21}!n_{22}!} \tag{17.7} \end{align}\]

Como exemplo, suponhamos que um estudo gerou a tabela 17.7.

Tabela 17.7: Tabela 2x2 com valores esperados muito pequenos nas células.

	Desfecho Clínico
Exposição	Sim	Não	Total
Nível 1	1	6	7
Nivel 2	5	3	8
Total	6	9	15

Supondo que os totais nas linhas e colunas sejam fixos (7, 8, 6, 9), então podem ser montadas 7 tabelas possíveis com esses totais (figura 17.3). A tabela 17.7 corresponde à segunda tabela (em negrito) na figura. Para cada tabela na figura 17.3, é mostrada a probabilidade de serem observados os seus valores, supondo que as variáveis sejam independentes. A partir das probabilidades de cada tabela, nós podemos calcular a probabilidade de obter a tabela observada, ou uma tabela menos provável, quando a hipótese nula é verdadeira.

Por exemplo, a probabilidade de se observar a tabela 17.7 é dada por:

\(\begin{aligned} &\ P(n_{11}=1)= \frac{7!6!8!9!}{15!1!6!5!3!} = 0,07832 \end{aligned}\)

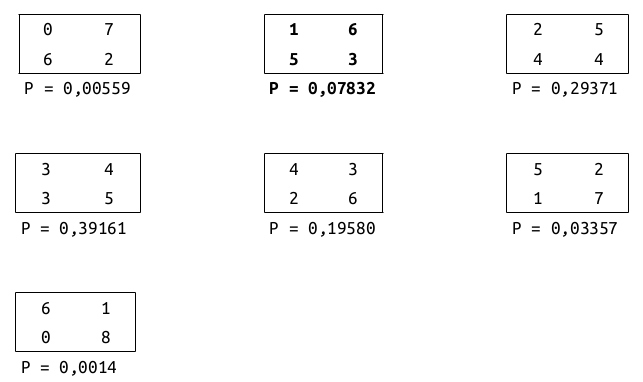
Figura 17.3: Todas as 7 tabelas possíveis de serem formadas, mantendo-se fixos os valores totais das linhas e colunas na tabela 17.7.

O valor de p do teste de Fisher-Irwin é obtido adicionando-se as probabilidades da tabela observada e de todas as demais que possuem probabilidades menores ou iguais à da tabela observada no estudo. A tabela observada possui probabilidade igual a 0,07832. As outras tabelas com probabilidades menores ou iguais a essa são as tabelas 1, 6 e 7 na figura 17.3. Logo:

valor de p = 0,07832 + 0,00559 + 0,03357 + 0,0014 = 0,1189

17.2.5.1 Teste exato de Fisher-Irwin no R

O conteúdo desta seção pode ser visualizado neste vídeo.

Pode-se realizar o teste exato de Fisher no R Commander para um certo conjunto de dados, seguindo o procedimento para realizar o teste qui ao quadrado mostrado na seção 8.3 do capítulo sobre medidas de associação. Nesta seção, vamos mostrar como realizar o teste exato de Fisher partindo diretamente da tabela 2x2, tomando como exemplo a tabela 17.7.

No R Commander, selecionamos a opção:

\[\text{Estatísticas} \Rightarrow \text{Tabelas de Contingência} \Rightarrow \text{Digite e analise tabela dupla entrada}\]

Na tela da figura 17.4, digitamos as células da tabela e selecionamos o teste exato de Fisher na aba Estatísticas (figura 17.5).

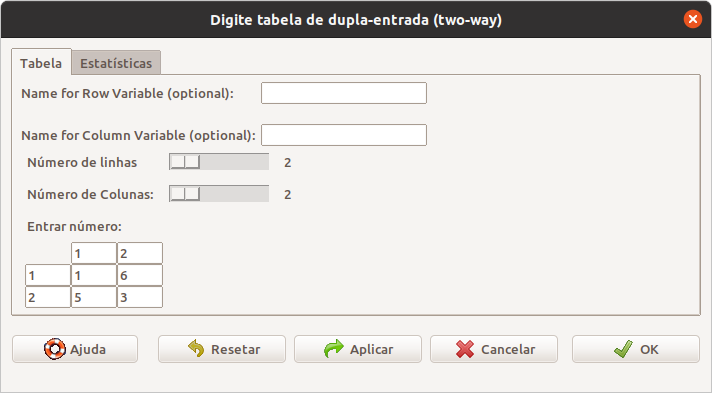
Figura 17.4: Entrada dos valores na tabela 2x2.

Figura 17.5: Seleção do teste exato de Fisher.

Os resultados são mostrados a seguir. Observem que primeiramente é realizado o teste qui ao quadrado de Pearson. Uma mensagem (não mostrada aqui) alerta que a aproximação pode estar incorreta. Ao final é mostrado o teste de Fisher, juntamente com a medida da razão de chances.

.Table <- matrix(c(1,6,5,3), 2, 2, byrow=TRUE)
dimnames(.Table) <- list("rows"=c("1", "2"), "columns"=c("1", "2"))

.Table  # Counts

##     columns
## rows 1 2
##    1 1 6
##    2 5 3

.Test <- chisq.test(.Table, correct=FALSE)
.Test

## 
##  Pearson's Chi-squared test
## 
## data:  .Table
## X-squared = 3.6161, df = 1, p-value = 0.05722

remove(.Test)
fisher.test(.Table)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  .Table
## p-value = 0.1189
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.001827082 1.768053629
## sample estimates:
## odds ratio 
##  0.1189474

remove(.Table)

Podemos ver que os valores de p, obtidos pelo teste de Fisher e pelo teste qui ao quadrado, são bastante diferentes, indicando que a aproximação do teste qui ao quadrado não é adequada neste exemplo.

17.3 Comparação de proporções em duas amostras dependentes

Os conteúdos desta seção e de suas subseções podem ser visualizados neste vídeo.

Nesta seção, consideraremos que as duas amostras, correspondentes aos níveis 1 e 2 do fator de exposição, ou correspondentes aos diferentes níveis do desfecho, não foram obtidas de maneira independente. Essa situação pode acontecer, por exemplo, nos seguintes casos:

1. Ensaio controlado randomizado cross-over: nesses estudos, o mesmo paciente experimenta os tratamentos investigados em sequência, de tal modo que cada paciente é o próprio controle;

2. Estudo de coortes onde, para cada indivíduo exposto ao fator em estudo, um indivíduo não exposto ao fator é selecionado com base em uma ou mais características cujos valores concordam com os valores do indivíduo exposto, utilizando um critério definido a priori, por exemplo, a idade do indivíduo não exposto não deve ser diferente daquela do indivíduo exposto por mais de dois anos e que ambos sejam do mesmo sexo. Dizemos que cada indivíduo não exposto foi pareado com um indivíduo exposto;

3. estudo de caso-controle onde, para cada caso, um controle é selecionado com base em uma ou mais características cujos valores concordam com os valores do caso. Dizemos que cada controle foi pareado com um caso.

Em todos esses casos, dizemos que as amostras são pareadas.

Supondo que estamos com um estudo de coortes, com o fator em estudo e o desfecho dicotômicos, onde cada indivíduo exposto ao fator em estudo foi pareado com outro indivíduo não exposto ao fator, num total de n pares, a tabela 2 x 2 usualmente é montada como mostra a tabela 17.8.

Tabela 17.8: Montagem de uma tabela 2x2 para comparação de proporções em estudos de coortes com amostras pareadas.

		Fator ausente
		Desfecho positivo	Desfecho negativo
Fator presente	Desfecho positivo	\(\textit{a}\)	\(\textit{b}\)	\(\textit{a+b}\)
Fator presente	Desfecho negativo	\(\textit{c}\)	\(\textit{d}\)	\(\textit{c+d}\)
		\(\textit{a+c}\)	\(\textit{b+d}\)	\(\textit{n = a+b+c+d}\)

A primeira célula da tabela, \(\textit{a}\), representa o número de pares onde os dois elementos do par tiveram o desfecho (ou o nível 1 do desfecho).

A segunda célula da tabela, \(\textit{b}\), representa o número de pares onde o elemento do par exposto ao fator (ou o nível 1 do fator) teve o desfecho (ou o nível 1 do desfecho) e o outro elemento do par não teve o desfecho (ou teve o nível 2 do desfecho).

A terceira célula da tabela, \(\textit{c}\), representa o número de pares onde o elemento do par exposto ao fator (ou o nível 1 do fator) não teve o desfecho (ou teve o nível 2 do desfecho) e o outro elemento do par teve o desfecho (ou o nível 1 do desfecho).

A quarta célula da tabela, \(\textit{d}\), representa o número de pares onde os dois elementos do par não tiveram o desfecho (ou tiveram o nível 2 do desfecho).

O total da tabela é o total de pares do estudo (n), ou 2n indivíduos.

Verifiquem a diferença entre essa tabela e a tabela para amostras independentes (tabela 17.1).

A partir da tabela 17.8, o risco do desfecho positivo entre os que possuem o fator é:

\(\begin{aligned} &\ p_1 = \frac{a+b}{n} \end{aligned}\)

O risco do desfecho positivo entre os que não possuem o fator é:

\(\begin{aligned} &\ p_2 = \frac{a+c}{n} \end{aligned}\)

Logo a diferença entre as duas proporções é dada por:

\[\begin{align} DAR = p_1 - p_2 = \frac{b-c}{n} \tag{17.8} \end{align}\]

O risco relativo é dado por:

\[\begin{align} RR = \frac{p_1}{p_2} = \frac{a+b}{a+c} \tag{17.9} \end{align}\]

A razão de chances é estimada por [Rothman, Greenland, and Lash (2011), página 286):

\[\begin{align} RC = \frac{b}{c} \tag{17.10} \end{align}\]

Para um estudo de caso-controle pareado, a tabela seria construída de maneira semelhante, apenas trocando as posições das variáveis fator de exposição e desfecho (tabela 17.9). A mesma fórmula (17.10) se aplica para o cálculo da razão de chances.

Tabela 17.9: Montagem de uma tabela 2x2 para comparação de proporções em um estudo de caso-controle com amostras pareadas.

		Desfecho negativo
		Fator presente	Fator ausente
Desfecho positivo	Fator presente	\(\textit{a}\)	\(\textit{b}\)	\(\textit{a+b}\)
Desfecho positivo	Fator ausente	\(\textit{c}\)	\(\textit{d}\)	\(\textit{c+d}\)
		\(\textit{a+c}\)	\(\textit{b+d}\)	\(\textit{n = a+b+c+d}\)

17.3.1 Teste de McNemar

Há diversos testes propostos para testar a hipótese nula de independência das variáveis em amostras pareadas. Fagerland et al. (Fagerland, Lydersen, and Laake 2014) discutem algumas delas. Vamos apresentar duas delas, possivelmente os dois testes mais frequentemente usados.

a) Teste de McNemar assintótico:

Para amostras suficientemente grandes, o erro padrão de p₁ - p₂ é dado por:

\(\begin{aligned} &\ EP(p_1-p_2) = \frac{\sqrt{b+c}}{n} \end{aligned}\)

e a estatística

\[\begin{align} \chi^2 = \left(\frac{p_1-p_2}{ EP[p_1-p_2]}\right)^2 = \frac{(b-c)^2}{b+c} \tag{17.11} \end{align}\]

segue uma distribuição qui ao quadrado com 1 grau de liberdade.

b) Teste de McNemar assintótico com correção de continuidade:

Este teste é semelhante ao anterior, porém com uma correção de continuidade:

\[\begin{align} \chi^2 = \left(\frac{|p_1-p_2|-1/n}{ EP[p_1-p_2]}\right)^2 = \frac{(|b-c|-1)^2}{b+c} \tag{17.12} \end{align}\]

A estatística \(\chi^2\) segue uma distribuição qui ao quadrado com 1 grau de liberdade.

Para se testar uma hipótese com um nível \(\alpha\) de significância, compara-se o valor obtido de (17.11) ou (17.12) com o valor correspondente a \(\chi^2_{1,\alpha}\).

17.3.2 Intervalos de confiança para a diferença de proporções, risco relativo e razão de chances

Para a estimativa dos intervalos de confiança para as medidas de associação expressas em (17.8), (17.9) e (17.10) também existem diversas propostas na literatura. Neste texto, vamos utilizar algumas recomendadas por Fagerland et al. (Fagerland, Lydersen, and Laake 2014).

17.3.2.1 Intervalo de confiança para a diferença de proporções

Um dos métodos recomendados por Fagerland et al. para o cálculo do intervalo de confiança para a diferença de proporções é chamado de Wald with Bonett–Price Laplace adjustment. Para o cálculo dos limites do intervalo de confiança, calcula-se inicialmente as duas quantidades:

\(\tilde{p_{12}} = \frac{b+1}{n+2}\), \(\tilde{p_{21}} = \frac{c+1}{n+2}\)

Então os limites do intervalo de confiança para p₁ - p₂ serão:

\(\begin{aligned} &\ P_i = (\tilde{p_{12}} - \tilde{p_{21}}) - z_{\alpha/2}\ \sqrt{\frac{\tilde{p_{12}}+\tilde{p_{21}}-(\tilde{p_{12}}-\tilde{p_{21}})^2}{n+2}} \end{aligned}\)

\(\begin{aligned} &\ P_s = (\tilde{p_{12}} - \tilde{p_{21}}) + z_{\alpha/2}\ \sqrt{\frac{\tilde{p_{12}}+\tilde{p_{21}}-(\tilde{p_{12}}-\tilde{p_{21}})^2}{n+2}} \end{aligned}\)

Limites fora do intervalo [-1, 1] são truncados.

17.3.2.2 Intervalo de confiança para o risco relativo

Um dos métodos recomendados por Fagerland et al. para o cálculo do intervalo de confiança para o risco relativo é chamado de Bonett–Price hybrid Wilson score.

Seja \(nd=a+b+c\) e definamos:

\(\begin{aligned} &\ A = \sqrt{\frac{b+c+2}{(a+b+1)(a+c+1)}} \end{aligned}\)

\(\begin{aligned} &\ B = \sqrt{\frac{1-\frac{a+b+1}{nd+2}}{(a+b+1)}} \end{aligned}\)

\(\begin{aligned} &\ C = \sqrt{\frac{1-\frac{a+c+1}{nd+2}}{(a+c+1)}} \end{aligned}\)

\(\begin{aligned} &\ z = \frac{A}{B+C}z_{\alpha/2} \end{aligned}\)

O intervalo do escore de Wilson para p₁ é dado por:

\(\begin{aligned} &\ [l_1, u_1] = \frac{2(a+b)+z^2 \pm \sqrt{z^2+4(a+b)\left(1-\frac{a+b}{nd}\right)}}{2(nd+z^2)} \end{aligned}\)

O intervalo do escore de Wilson para p₂ é dado por:

\(\begin{aligned} &\ [l_2, u_2] = \frac{2(a+c)+z^2 \pm \sqrt{z^2+4(a+c)\left(1-\frac{a+c}{nd}\right)}}{2(nd+z^2)} \end{aligned}\)

Finalmente o intervalo do risco relativo pelo método de Bonett–Price hybrid Wilson score é dado por:

\(\begin{aligned} &\ [RR_i, RR_s] = \left[\frac{l_1}{u_2}, \frac{u_1}{l_2}\right] \end{aligned}\)

17.3.2.3 Intervalo de confiança para a razão de chances

Um dos métodos recomendados por Fagerland et al. para o cálculo do intervalo de confiança para a razão de chances é chamado de Transformed Wilson score. Por esse método, calcula-se inicialmente os valores de L e S por meio da expressão abaixo:

\([L, S] = \frac{2b + z_{\alpha/2}^2 \pm z_{\alpha/2}\ \sqrt{ z_{\alpha/2}^2 + 4b\left(1-\frac{b}{b+c}\right)}}{2\left(b+c+ z_{\alpha/2}^2 \right)}\)

O intervalo de confiança para a razão de chances é dado então por:

\([RC_i, RC_s] = \left[\frac{L}{1-L}, \frac{S}{1-S}\right]\)

17.3.3 Comparação de proporções entre duas amostras dependentes no R

O pacote stats no R possui uma função chamada mcnemar.test que realiza as duas versões do teste de McNemar apresentadas na seção 17.3.1. O parâmetro correct = TRUE realiza o teste com a correção de continuidade, enquanto se fizermos correct = FALSE, o teste será realizado sem a correção de continuidade. Se nada for especificado, a função assumirá que correct = TRUE. Essa função não calcula os intervalos de confiança para as medidas de associação. Vide a ajuda para o teste de McNemar para verificar como utilizá-lo.

Uma função que tanto realiza o teste de McNemar quanto calcula os intervalos de confiança apresentados nas seções anteriores é a função paired_proportions, disponibilizada neste arquivo, cujo código fonte é mostrado no apêndice B.

Vamos supor que o arquivo paired_proportions.R tenha sido baixado na pasta temp do disco C do Windows. Para carregar esse arquivo e disponibilizar a função paired_proportions para ser utilizada numa sessão do R, podemos executar o comando a seguir:

source("C:\\temp\\paired_proportions.R")

Vamos ilustrar o uso da função paired_proportions, utilizando o conjunto de dados backpain do pacote HSAUR2 (GPL-2). Para instalar o pacote HSAUR2, use a função:

install.packages("HSAUR2")

Ao solicitarmos a ajuda para o conjunto de dados backpain, obtemos a figura 17.6.

Figura 17.6: Descrição das variáveis do conjunto de dados backpain do pacote HSAUR2.

O conjunto de dados backpain contém dados de um estudo de caso-controle para investigar se dirigir um carro é um fator de risco para dor lombar resultante de hérnia de disco intervertebral lombar aguda.

Os casos foram selecionados de pessoas que fizeram radiografias da parte inferior das costas e foram diagnosticadas como portadoras de hérnia de disco intervertebral lombar aguda.

Os controles foram retirados de pacientes internados no mesmo hospital que um caso com uma condição não relacionada à coluna vertebral e também pareados em idade e sexo, num total de 217 pares, consistindo de 89 pares femininos e 128 pares masculinos.

As variáveis no conjunto de dados são:
status – indica se o indivíduo é um caso ou um controle;
driver - indica se o indivíduo dirigia ou não;
suburban - indica se o indivíduo morava no subúrbio ou não;
ID - indica o par de indivíduos. Cada um dos 217 pares de indivíduos recebe um valor de ID diferente.

A presença da variável ID indica que se trata de um estudo com amostras pareadas.

A figura 17.7 mostra parte dos dados. Observem que cada valor de ID está associado a dois indivíduos, um caso e um controle.

Figura 17.7: Parte do conjunto de dados backpain do pacote HSAUR2.

Em seguida, execute a sequência de comandos a seguir para realizar o teste de McNemar e calcular o intervalo de confiança para a razão de chances.

library(HSAUR2)
data("backpain", package = "HSAUR2")
source('paired_proportions.R')
paired_proportions(data=backpain, id='ID', row='driver', col='status', 
                   row_ref='no', row_trt='yes', col_ref='control', 
                   col_out='case', case_control=TRUE, alpha=0.05)

##      control
## case  yes no
##   yes 144 41
##   no   19 13
## 
##  McNemar's Chi-squared test with continuity correction
## 
## data:  mat
## McNemar's chi-squared = 7.35, df = 1, p-value = 0.006706
## 
##   odds ratio Lower 95% CI Upper 95% CI 
##     2.157895     1.260716     3.693543

Para utilizar a função paired_proportions, o usuário deve carregar a função no R, por meio da função source, especificando entre aspas simples ou duplas o caminho no sistema de arquivos e o nome do arquivo que contém a função. No comando acima, o caminho foi especificado de acordo com a sintaxe do sistema operacional Linux.

Na chamada da função, o usuário deve especificar os seguintes parâmetros:

data - o data.frame a ser utilizado;
id – identificação dos pares – deve ser um variável da classe factor;
row – variável de exposição;
col – variável de desfecho;
row_ref – nível de referência da variável de exposição;
row_trt– outro nível de variável de exposição;
col_ref – nível de referência da variável de desfecho;
col_out – outro nível da variável de desfecho;
case_control – indica se o estudo é de caso-controle (TRUE) ou não (FALSE). O padrão é FALSE;
alpha – nível de significância (o padrão é 0,05).

A primeira saída da função monta a tabela 2x2 na forma semelhante à apresentada na tabela 17.9. Em seguida, os resultados do teste de McNemar são apresentados, seguido do intervalo de confiança para a razão de chances. Como os dados de backpain são relativos a um estudo de caso-controle e o pareamento foi baseado na variável de desfecho (status), os intervalos de confiança para a diferença de proporções e risco relativo não são apresentados.

Nesse exemplo, o valor de alfa foi de 5% e o teste de McNemar foi realizado com correção de continuidade. Caso se deseje outro nível de confiança, especifique o valor de alfa correspondente na variável alpha. Para não utilizar a correção de continuidade, especifique o parâmetro correct = FALSE. O exemplo abaixo utiliza o nível de confiança igual a 90% (alpha = 0.1) e não utiliza a correção de continuidade:

paired_proportions(backpain, 'ID', 'driver', 'status', 'no','yes','control', 
                   'case', case_control=TRUE, alpha = 0.1, correct = FALSE)

##      control
## case  yes no
##   yes 144 41
##   no   19 13
## 
##  McNemar's Chi-squared test
## 
## data:  mat
## McNemar's chi-squared = 8.0667, df = 1, p-value = 0.004509
## 
##   odds ratio Lower 90% CI Upper 90% CI 
##     2.157895     1.372335     3.393129

17.4 Poder estatístico e tamanho amostral

Ao planejar um estudo, é importante estimar previamente o tamanho amostral para que o teste de hipótese utilizado tenha um certo poder estatístico ou o intervalo de confiança tenha uma certa precisão.

Pode-se estimar o tamanho amostral para estudos em que uma única proporção esteja envolvida, quando duas proporções são comparadas em duas amostras independentes ou quando as amostras são pareadas, ou em casos mais genéricos. Não vamos considerar aqui todas as possibilidades. Vamos ilustrar o uso do R para o cálculo do tamanho amostral e poder estatístico para o caso de um estudo experimental onde duas amostras independentes são utilizadas.

Suponhamos que um estudo esteja sendo planejado para comparar um tratamento padrão com um tratamento experimental para um determinado tipo de câncer e o desfecho principal seja se houve ou não a remissão da doença após um determinado intervalo de tempo. Um certo número de pacientes serão submetidos ao tratamento padrão e o mesmo número será submetido ao tratamento experimental. Para estimar o tamanho amostral desse estudo, ou seja, o número n de pacientes em cada grupo, vamos partir das seguintes suposições:

1. Seja p₁ a proporção de pacientes que esperamos ter remissão da doença com o tratamento padrão;

2. Seja p₂ a proporção de pacientes que esperamos ter remissão da doença com o tratamento experimental;

3. Seja \(\alpha\) o nível de significância do teste e \(1 - \beta\) o poder estatístico do teste para detectar a diferença p₂ – p₁, caso ela realmente exista.

A partir dos dados acima, calculamos a média das duas proporções:

\(\begin{aligned} &\ \bar{p} = \frac{p_1 + p_2}{2} \end{aligned}\)

Fleiss (Fleiss 1981, página 41) apresenta a seguinte fórmula para o cálculo do tamanho amostral, quando a correção de continuidade no teste estatístico não é utilizada:

\[\begin{align} n = \left (\frac{(c_{1-\alpha/2}\ \sqrt{2\bar{p}(1-\bar{p})}-c_{1-\beta}\ \sqrt{p_1(1-p_1)+p_2(1-p_2)}}{p_2 - p_1}\right)^2 \tag{17.13} \end{align}\]

onde \(c_{1-\alpha/2}\) corresponde à probabilidade \(P (Z > c_{1-\alpha/2}) = \alpha/2\) (quantil \(1 - \alpha/2\)) na distribuição normal e \(c_{1- \beta}\) à probabilidade \((P (Z > c_{1- \beta}) = 1 - \beta\) (quantil \(\beta\)).

Vamos supor que p₁ = 0,60; p₂ = 0,70, \(\alpha\) = 5% e \(1-\beta\) = 80%.

Então:

  \(0,025 = P(Z > c_{1-\alpha/2} ) = P(Z > c_{0,975})\ \Rightarrow \ c_{0,975} = 1,96\) e

  \(0,80 = P(Z > c_{1- \beta}) = P(Z > c_{0,80})\ \Rightarrow\ c_{0,80} = 0,84\)

\(\begin{aligned} &\ n = \frac{(1,96\ \sqrt{2\ .\ 0,65\ .\ 0,35)}- 0,84\ \sqrt{0,6\ .\ 0,4 + 0,7\ .\ 0,3})^2}{(0,1)^2} = 356 \end{aligned}\)

17.4.1 Usando o R Commander para calcular o tamanho amostral

No R Commander, vamos carregar o plugin RcmdrPlugin.EZR. Para isso, selecionamos no menu a opção:

\[\text{Ferramentas} \Rightarrow \text{Carregar plug-in(s) do Rcmdr...}\]

Na tela com a lista de plugins disponíveis, selecionamos o RcmdrPlugin.EZR e pressionamos o botão OK (figura 17.8). Será preciso reiniciar o R Commander.

Figura 17.8: Selecionando o RcmdrPlugin.EZR.

Após a reinicialização do R Commander, selecionamos a opção:

\[\text{Stat. Analysis} \Rightarrow \text{Calc. sample size} \Rightarrow \text{Calc. sample size for comp. between two proportions}\]

A figura 17.9 mostra a tela para configurar os parâmetros para o cálculo do tamanho amostral. Nessa figura, configuramos os parâmetros de acordo com o exemplo ao final da seção anterior. Como as duas amostras são iguais, colocamos o parâmetro Sample size ratio igual a 1.

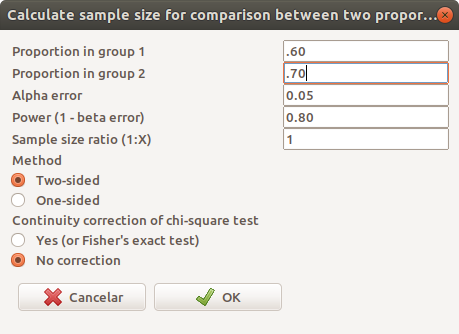
Figura 17.9: Configurando os parâmetros para o cálculo do tamanho amostral para o exemplo usado neste texto.

Ao clicarmos em OK na figura 17.9, o resultado é mostrado no R Commander, sendo o mesmo resultado obtido ao aplicarmos a fórmula (17.13). Além do resultado numérico, o R Commander exibe um gráfico que mostra o poder estatístico para diferentes valores de n (figura 17.10). A linha pontilhada horizontal corresponde ao poder estatístico igual a 80%.

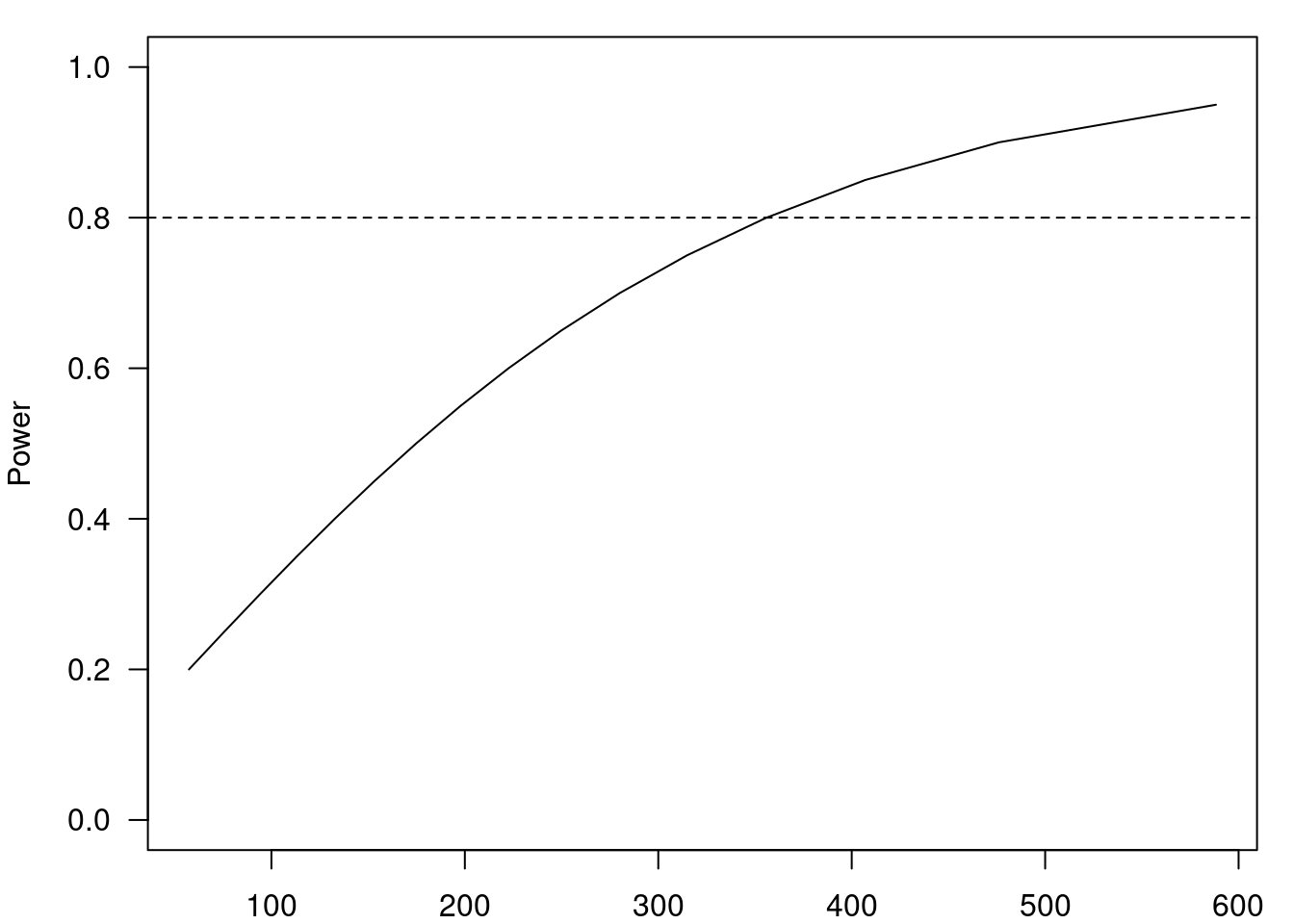
Figura 17.10: Tamanho amostral estimado para o exemplo considerado nesta seção.

##                      Assumptions
## P1                           0.6
## P2                           0.7
## Alpha                       0.05
##                        two-sided
## Power                        0.8
## N2/N1                          1
##                                 
## Required sample size   Estimated
## N1                           356
## N2                           356

Continuando o exemplo anterior, vamos supor que o grupo experimental foi planejado para ter 1,5 vezes o número de pacientes do grupo do tratamento padrão. Então, modificando a figura 17.9 e fazendo Sample size ratio igual 1,5 (figura 17.11), obtemos o resultado mostrado na figura 17.12.

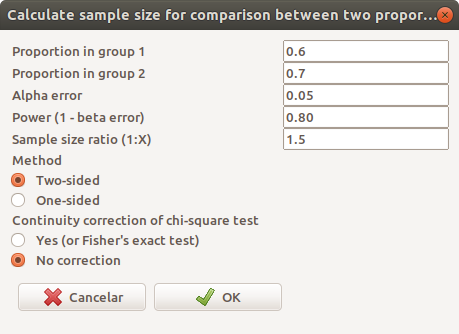
Figura 17.11: Alterando a razão entre o número de pacientes em cada grupo de tratamento para 1,5.

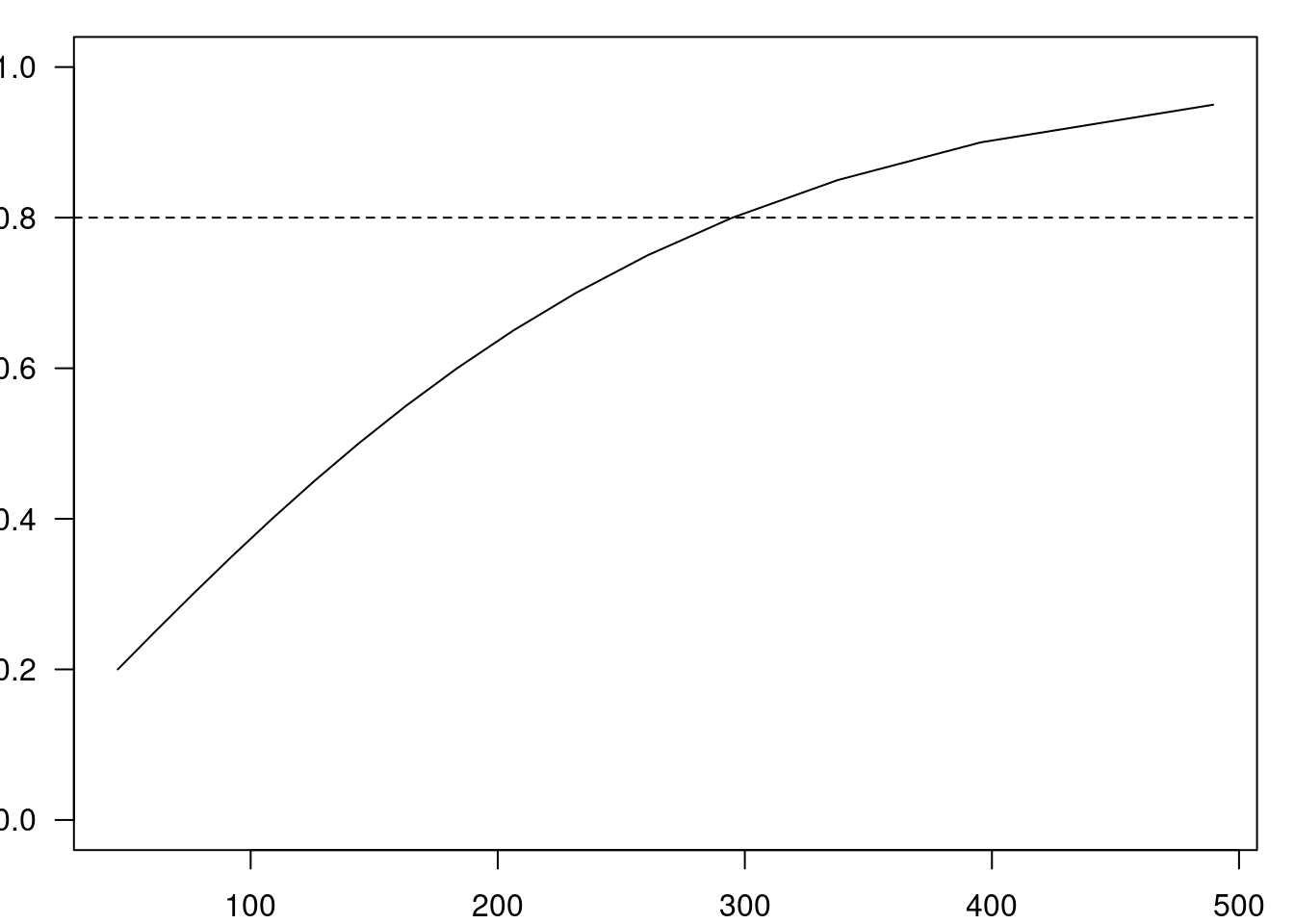
Figura 17.12: Tamanho amostral estimado para a configuração mostrada na figura 17.11.

##                      Assumptions
## P1                           0.6
## P2                           0.7
## Alpha                       0.05
##                        two-sided
## Power                        0.8
## N2/N1                        1.5
##                                 
## Required sample size   Estimated
## N1                           295
## N2                         442.5

Alternativamente, conhecendo-se o tamanho amostral, pode-se estimar o poder estatístico de um teste que compara duas proporções em duas amostras independentes por meio da opção:

\[\text{Stat. Analysis} \Rightarrow \text{Calc. sample size} \Rightarrow \text{Calc. power for comp. between two prop.}\]

Na tela de configuração dos parâmetros (figura 17.13), vamos utilizar as mesmas proporções, erro \(\alpha\) e erro \(\beta\) dos exemplos anteriores e vamos supor que os dois grupos tenham 40 pacientes.

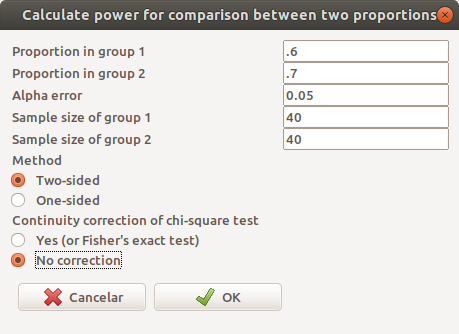
Figura 17.13: Configuração dos parâmetros para o cálculo do poder estatístico a partir do tamanho amostral.

Ao pressionarmos o botão OK, obtemos a curva poder estatístico x tamanho amostral (figura 17.14) e o poder estatístico igual a 15,2% para a configuração da figura 17.13, um valor bastante baixo.

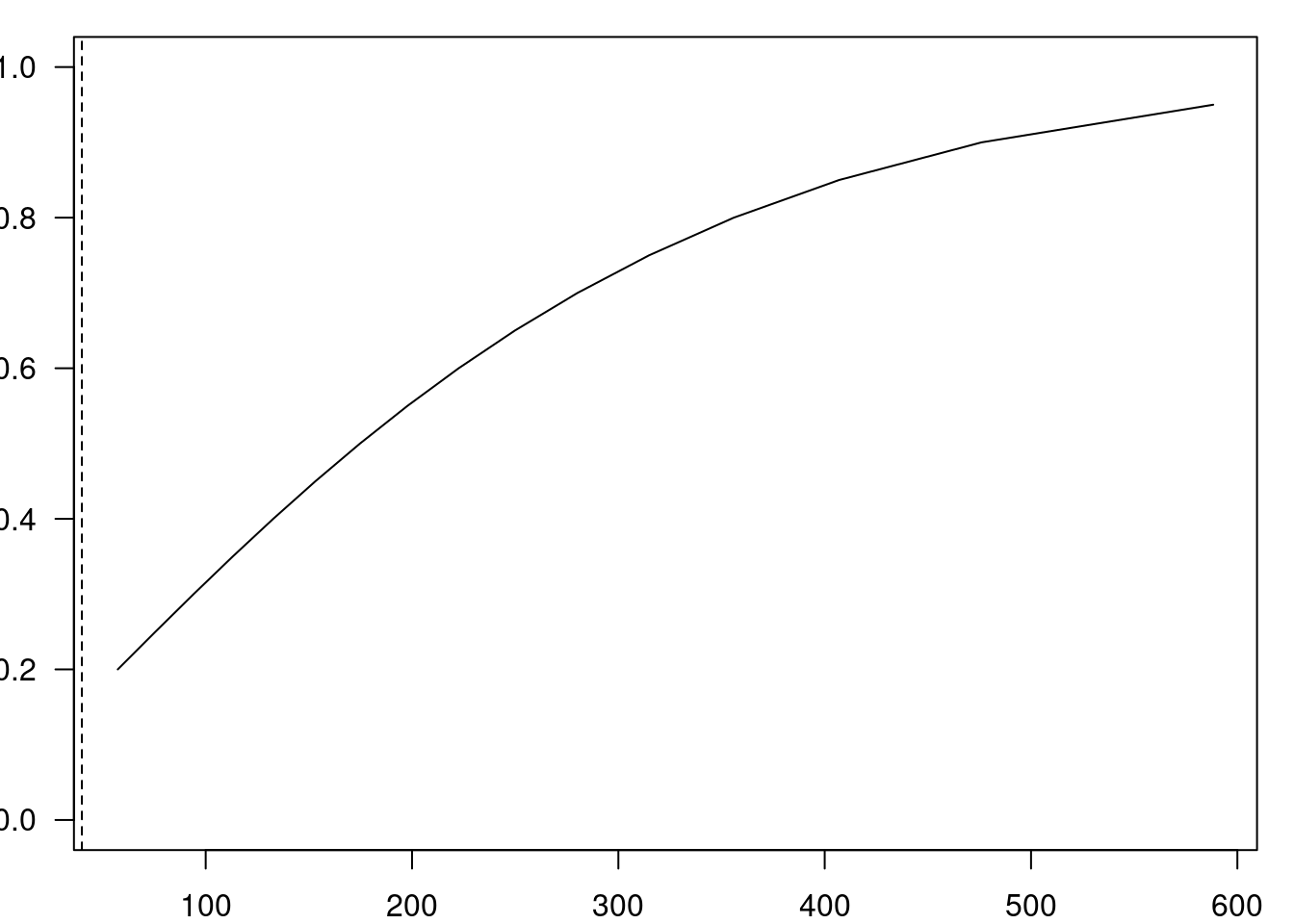
Figura 17.14: Poder estatístico de um teste de comparação de duas proporções com as configurações mostradas na figura 17.13.

##             Assumptions
## P1                  0.6
## P2                  0.7
## Alpha              0.05
##               two-sided
## Sample size            
## N1                   40
## N2                   40
##                        
##               Estimated
## Power             0.152

17.5 Tabelas r x c

Os conteúdos desta seção e da subseção 17.5.1 podem ser visualizados neste vídeo.

Nesta seção, iremos considerar a situação onde as variáveis de exposição e desfecho tenham r e c categorias (r ou c > 2), respectivamente, em vez de somente duas categorias, como nas seções anteriores. Vamos considerar somente o caso onde as amostras são independentes. No caso mais geral, uma tabela r x c (r linhas e c colunas) terá a estrutura conforme a tabela 17.10.

Tabela 17.10: Tabela r x c que verifica a associação entre duas variáveis categóricas com r e c níveis respectivamente.

	Desfecho Clínico
Exposição	Nível 1		Nível c	Total
Nível 1	n11	…	n1c	n1+=n11+…+n1c
…	…	…	…	…
Nivel r	nr1	…	nrc	nr+ =nr1+…+nrc
Total	n+1 = n11 + … + nr1	…	n+c=n1c+…+nrc	n=n1+ +…+nr+

As proporções em cada célula da tabela 17.11 são calculadas a partir da tabela 17.10, dividindo-se a frequência em cada célula pela soma de todas as frequências (n) da tabela.

Tabela 17.11: Proporções em cada célula da tabela 17.10, obtidas por meio da divisão da frequência de cada célula por n.

	Desfecho Clínico
Exposição	Nível 1		Nível c	Total
Nível 1	p11	…	p1c	p1+ =p11+…+p1c
…	…	…	…	…
Nivel r	pr1	…	prc	pr+ =pr1+…+prc
Total	p+1=p11+…+pr1	…	p+c=p1c+…+prc	p=p1+ +…+pr+

Sob a hipótese de independência das variáveis Exposição e Desfecho, a proporção esperada em cada célula seria dada pela expressão:

  \(p_{ij} = p_{i+}p_{+j}\), i = 1, …, r;   j =1,…, c

e a frequência esperada em cada célula é calculada de acordo com a tabela 17.12.

Tabela 17.12: Valores esperados em cada célula da tabela 17.10, sob a hipótese de independência.

	Desfecho Clínico
Exposição	Nível 1		Nível c	Total
Nível 1	E11 = (n1+ n+1)/n	…	E1c = (n1+ n+c)/n	n1+
…	…	…		…
Nivel r	Er1 = (nr+ n+1)/n	…	Erc = (nr+ n+c)/n	nr+
Total	n+1	…	n+c	n

Sob a hipótese nula (independência dos eventos), espera-se que os valores observados não sejam muito diferentes dos valores esperados. A estatística abaixo, generalização da expressão (17.3), segue aproximadamente uma distribuição qui ao quadrado, com (r-1)(c-1) graus de liberdade, quando a hipótese nula é verdadeira. Assim valores suficientemente altos de \(\chi^2\) levam à rejeição da hipótese nula.

\[\begin{align} \chi^2 = \sum_{i=1}^{r}\sum_{j=1}^{c}\frac{(O_{ij}-E_{ij})^2}{E_{ij}} \tag{17.14} \end{align}\]

A aproximação (17.14) é válida para valores suficientemente grandes nas células da tabela. Entretanto o que pode ser considerado “suficientemente grande” é uma questão aberta. Uma recomendação frequentemente citada é que o teste qui ao quadrado não deve ser usado caso uma frequência esperada seja menor que 2 ou se mais de 20% das frequências esperadas forem menores que 5 (Dawson and Trapp 2001). Nesses casos, deve-se usar o teste exato de Fisher, ou usar uma estratégia de reduzir o número de categorias em cada variável.

Como temos reforçado nesse texto, o teste de hipótese é apenas um dos elementos da análise estatística. Mais importante em uma tabela r x c é verificar os valores das medidas de associação e os respectivos intervalos de confiança. Há que se considerar que mais variáveis podem afetar as associações observadas em uma tabela r x c (que contém somente duas variáveis). Análises mais sofisticadas envolvendo variáveis categóricas utilizam modelagem estatística para identificar padrões nos dados observados. Esses modelos estão fora do escopo deste texto (Agresti 1996).

17.5.1 Análise de uma tabela r x c no R Commander

Vamos utilizar o conjunto de dados bacteria do pacote MASS (Venables and Ripley 2002) (GPL-2 | GPL-3). Esse conjunto de dados contém dados sobre testes sobre a presença da bactéria H. influenzae em crianças com otite média no norte da Austrália. As crianças foram randomizadas em três tratamentos (variável trt): placebo, medicamento (drug) e medicamento + encorajamento (drug+) para tomar o medicamento. A variável y indica a presença ou não de bactéria.

A presença de bactérias é investigada antes de iniciar o tratamento, na segunda, na quarta, na sexta e na décima-primeira semanas após o início do tratamento.

Vamos analisar a relação entre as variáveis tratamento e presença ou não de bactéria na 6^a semana.

Após carregarmos o conjunto de dados bacteria, reordenamos os níveis das variáveis y e trt:

bacteria$y <- with(bacteria, factor(y, levels=c('y','n')))
bacteria$trt <- with(bacteria, factor(trt, 
                                      levels=c('drug+','drug','placebo')))

Em seguida, selecionamos a opção do menu do R Commander:

\[\text{Estatísticas} \Rightarrow \text{Tabelas Contingência} \Rightarrow \text{Tabela de dupla entrada}\]

Na caixa de diálogo da figura 17.15, selecionamos a variável cujas categorias aparecerão nas linhas da tabela (em geral a variável de exposição) e a variável cujas categorias aparecerão nas colunas da tabela (em geral a variável de desfecho). No campo expressão (subset expression), digitamos a expressão lógica “week == 6” para incluir na análise somente os registros da 6^a semana.

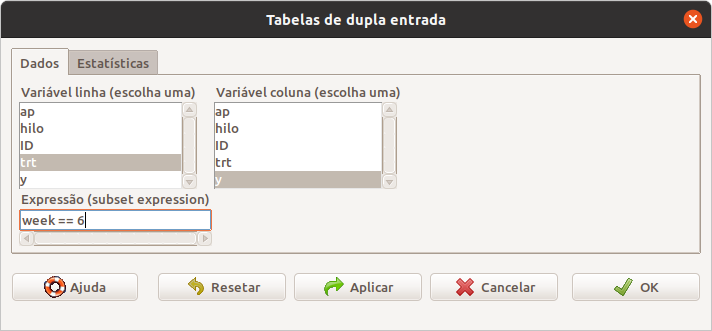
Figura 17.15: Selecionando as duas variáveis para o teste qui ao quadrado para uma tabela r x c e os registros que serão incluídos na análise.

Em seguida, na aba Estatísticas, o usuário seleciona o modo como a tabela será apresentada e os testes estatísticos (qui ao quadrado e/ou teste exato de Fisher, figura 17.16).

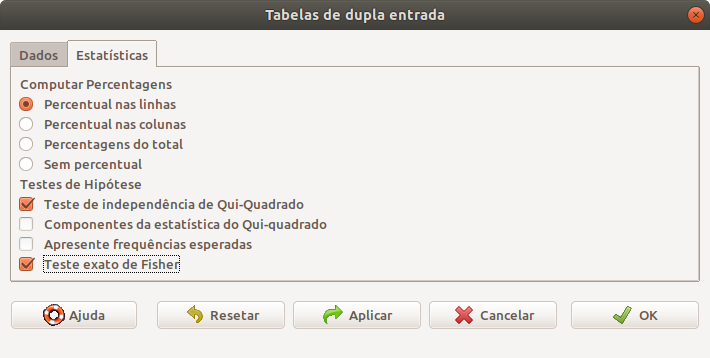
Figura 17.16: Selecionando os testes que serão realizados, bem como que percentuais serão mostrados a partir do teste qui ao quadrado para uma tabela r x c.

Ao clicarmos no botão OK, os resultados são apresentados.

## 
## Frequency table:
##          y
## trt        y  n
##   drug+    7  5
##   drug     6  5
##   placebo 16  1
## 
## Row percentages:
##          y
## trt          y    n Total Count
##   drug+   58.3 41.7   100    12
##   drug    54.5 45.5   100    11
##   placebo 94.1  5.9   100    17
## 
##  Pearson's Chi-squared test
## 
## data:  .Table
## X-squared = 6.9712, df = 2, p-value = 0.03064
## 
## 
##  Fisher's Exact Test for Count Data
## 
## data:  .Table
## p-value = 0.03146
## alternative hypothesis: two.sided

Foram identificadas bactérias em 94 % das crianças do grupo placebo, em apenas 54% das crianças no grupo medicamento e em 58% do grupo medicamento + estímulo para ingerir o medicamento.

O valor de p obtido por meio do teste qui ao quadrado é semelhante ao obtido pelo teste exato de Fisher. Usando o nível de significância de 5%, a hipótese nula de independência entre tratamento e presença de bactéria é rejeitada.

A análise deverá prosseguir para verificar os efeitos dos tratamentos e respectivos intervalos de confiança, mas também deverá considerar os outros instantes de tempo onde a presença de bactérias foram identificadas.

17.6 Exercícios

1. Com o conjunto de dados birthwt do pacote MASS (GPL-2 | GPL-3), faça as atividades abaixo.

   1. Obtenha as medidas de associação DAR, RR e RC e os respectivos intervalos de confiança ao nível de 95% para a relação entre as variáveis smoke (mãe fumante ou não durante a gravidez) e low (indicador de baixo peso ao nascer). Discuta os resultados em termos de força e precisão das medidas.
   2. Repita o item “a” para as variáveis ht (histórico de hipertensão da mãe) e low.

2. Com o mesmo conjunto de dados da questão 1, verifique a associação entre as variáveis race (raça da mãe) e low.

3. O conjunto de dados retinopathy do pacote survival (LGPL-2 | LGPL-2.1 | LGPL-3) contém dados sobre um ensaio de coagulação a laser como tratamento para atrasar a retinopatia diabética. Cada paciente teve um dos olhos tratados com um dos dois tipos de laser: xenônio ou argônio. A variável trt indica qual dos olhos de cada paciente foi tratado (0 = olho controle, 1 = olho tratado), a variável status indica se houve perda de visão no olho correspondente até o final do acompanhamento no estudo (0 = censurado, 1 = perda de visão) e a variável id identifica cada paciente (dois registros por paciente, um para cada olho). Use a função paired_proportions (seção 17.3.3) para verificar a associação entre o fato de um olho ser ou não tratado com ocorrência da perda de visão. A variável nas linhas é trt, a variável nas colunas é status, os níveis das variáveis trt e status são numéricos e o estudo não é um estudo de caso-controle (é um ensaio controlado randomizado). É preciso converter a variável id para fator. Obtenha as medidas de associação DAR, RR e RC e os respectivos intervalos de confiança ao nível de 90%. Discuta os resultados.

4. Considere o artigo “Estudo clínico, duplo-cego, randomizado, em crianças com amigdalites recorrentes submetidas a tratamento homeopático”, cujos resultados são apresentados na figura 17.17. Vamos analisar a associação entre os tipos de tratamento e a ocorrência de amigdalite, tomando o placebo como referência. Responda às questões abaixo.

   1. Você considera a apresentação dos resultados satisfatória? Justifique.
   2. Obtenha as medidas de associação DAR, RR e RC para esse estudo e os respectivos intervalos de confiança?
   3. Qual é a interpretação para o intervalo de confiança da DAR?
   4. Qual é o valor de p para essa associação. O que você pode dizer a respeito da significância estatística desse resultado?
   5. O que você tem a comentar sobre a precisão da estimativa da diferença absoluta de riscos?
   6. Obtenha o NNT para esse estudo.

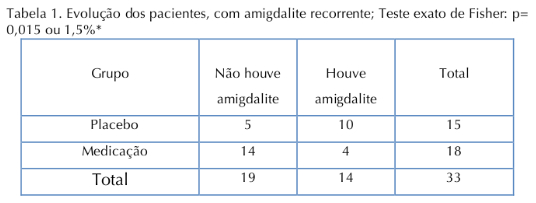
Figura 17.17: Tabela 1 do estudo de (Furuta, Weckx, and Figueiredo 2017) (CC BY).

5. Suponha que diversos ensaios controlados randomizados comparam o efeito de dois tratamentos A e B sobre um desfecho clínico dicotômico. Considere também que os estudos não apresentam nenhuma evidência de tendenciosidades e os tratamentos comparados não são os mesmos de estudo para estudo. Os resultados dos estudos são mostrados na figura 17.18 a seguir.

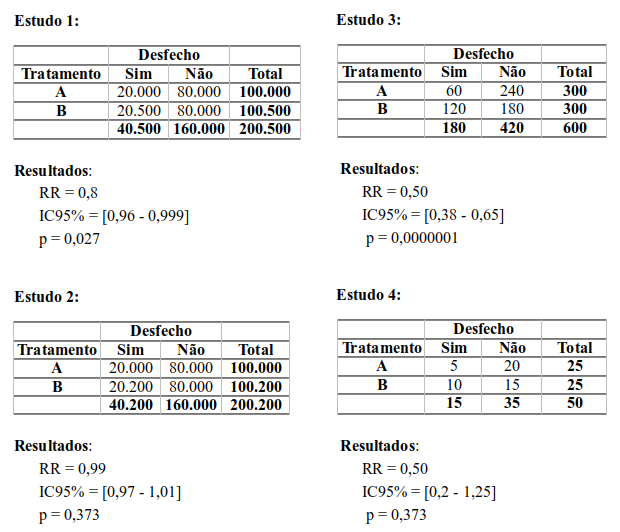
Figura 17.18: Diferentes resultados gerados a partir de tabelas 2x2.

Discuta cada resultado separadamente. A seguir, a partir de uma comparação dos resultados, comente a possível incidência de erro tipo I ou tipo II em cada estudo, as limitações de testes de hipótese e o valor de p e o efeito do tamanho amostral sobre os resultados.

Referências

Agresti, A. 1996. An Introduction to Categorical Data Analysis. New York: John Wiley & Sons, Inc.

Campbell, I. 2007. “Chi-Squared and Fisher–Irwin Tests of Two-by-Two Tables with Small Sample Recommendations.” Statistics in Medicine 26: 3661–75. https://doi.org/10.1002/sim.2832.

Dawson, B, and RG Trapp. 2001. Bioestatística Básica e Clínica. 3rd ed. Rio de Janeiro - Brazil: McGraw-Hill Interamericana do Brasil Ltd.

Fagerland, MW, S Lydersen, and P Laake. 2014. “Recommended Tests and Confidence Intervals for Paired Binomial Proportions.” Statistics in Medicine 33: 2850–75.

Fleiss, JL. 1981. Statistical Methods for Rates and Proportions. 2nd ed. New York: John Wiley & Sons.

Furuta, S E, Luc Louis Maurice Weckx, and C R Figueiredo. 2017. “Estudo Clínico, Duplo-Cego, Randomizado, Em Crianças Com Amigdalites Recorrentes Submetidas a Tratamento Homeopático.” Revista de Homeopatia 80 (1/2): 164–73.

Hjerkind, Kirsti Vik, Jo S Stenehjem, and Tom I L Nilsen. 2017. “Adiposity, Physical Activity and Risk of Diabetes Mellitus: Prospective Data from the Population-Based HUNT Study, Norway.” BMJ Open 7: e013142. https://doi.org/10.1136/bmjopen-2016-013142.

Pearson, ES. 1947. “The Choice of Statistics Tests Illustrated on the Interpretation of Data Classed in a 2 × 2 Table.” Biometrika 34 (1/2): 139–67.

Pearson, K. 1900. “On the Criterion That a Given System of Deviations from the Probable in the Case of a Correlated System of Variables Is Such That It Can Be Reasonably Supposed to Have Arisen from Random Sampling.” Philosophical Magazine Series, 5th series, 50 (302): 157–75.

Rothman, Kenneth J, Sander Greenland, and Timothy L Lash. 2011. Epidemiologia Moderna. 3rd ed. Porto Alegre: Artmed.

Severo, Isis Marques, Ricardo Souza Kuchenbecker, Débora Feijó Villas Boas Vieira, Amália Fátima Lucena, and Miriam Abreu Almeida. 2018. “Fatores de Risco Para Quedas Em Pacientes Adultos Hospitalizados: Um Estudo Caso-Controle.” Revista Latino-Americana de Enfermagem 26 (e3016). https://doi.org/http://dx.doi.org/10.1590/1518-8345.2460.3016.

Venables, WN, and BD Ripley. 2002. Modern Applied Statistics with S. 4th ed. New York: Springer. http://www.stats.ox.ac.uk/pub/MASS4.

Yates, F. 1934. “Contingency Tables Involving Small Numbers and the X2 Test.” Journal of the Royal Statistical Society 1 Supplement: 217–35.