3 Medidas de tendência central e dispersão

3.1 Introdução

Os conteúdos desta seção e das suas subseções podem ser visualizados neste vídeo.

Abaixo são apresentados os valores das variáveis idade gestacional, crib (Clinical Risk Index for Babies), fração inspirada de O₂ máxima (fiO2_maximo), peso ao nascimento e óbito de 10 recém-nascidos tratados em uma UTI neonatal. Esse arquivo de dados, chamado neonato, contém dados de mais de 300 recém-nascidos. Há uma série de outras variáveis que foram coletadas para esses recém-nascidos, mas não foram mostradas. Os dados apresentados de uma forma tabular não nos fornece uma boa ideia de como estão distribuídos e suas principais características.

##    ig_parto crib fio2_maximo peso_nascimento obito
## 1       232    2          NA            1185    No
## 3       235   NA          NA            1500    No
## 4       200    1          NA            1110    No
## 5       218   NA          21            1315    No
## 6       248   NA          21            1390    No
## 7       205   10         100             980    No
## 9       219   NA          30            1060    No
## 10      221    1          60            1095   Yes
## 11      186   16         100             500   Yes
## 12      211    1          60            1255   Yes

O primeiro passo para realizar uma análise de dados envolve a inspeção das variáveis individualmente. Essa exploração dos dados pode ser realizada por meio de tabelas de contingência para variáveis categóricas (capítulo 2), ou por meio de medidas numéricas para variáveis numéricas, além de recursos gráficos para ambos os tipos de variáveis. Os principais recursos gráficos serão apresentados no capítulo 4. Para as variáveis numéricas, as medidas numéricas mais utilizadas são as de localização (tendência central) e de dispersão.

Um gráfico bastante utilizado para mostrar a distribuição dos valores de uma variável numérica é o histograma que, de uma maneira resumida, mostra a frequência ou percentual dos valores em cada faixa de valores da variável numérica. A figura 3.1 mostra o histograma de frequência da variável idade gestacional do conjunto de dados neonato (gráfico superior) e da variável crib (gráfico inferior). As retas perpendiculares em ambos os gráficos indicam a média (vermelha) e a mediana (azul), respectivamente. As médias e medianas serão discutidas mais adiante. Especialmente o segundo histograma indica uma uma assimetria à direita no gráfico. Os valores das médias e medianas não coincidem e são razoavelmente distintos no histograma do crib.

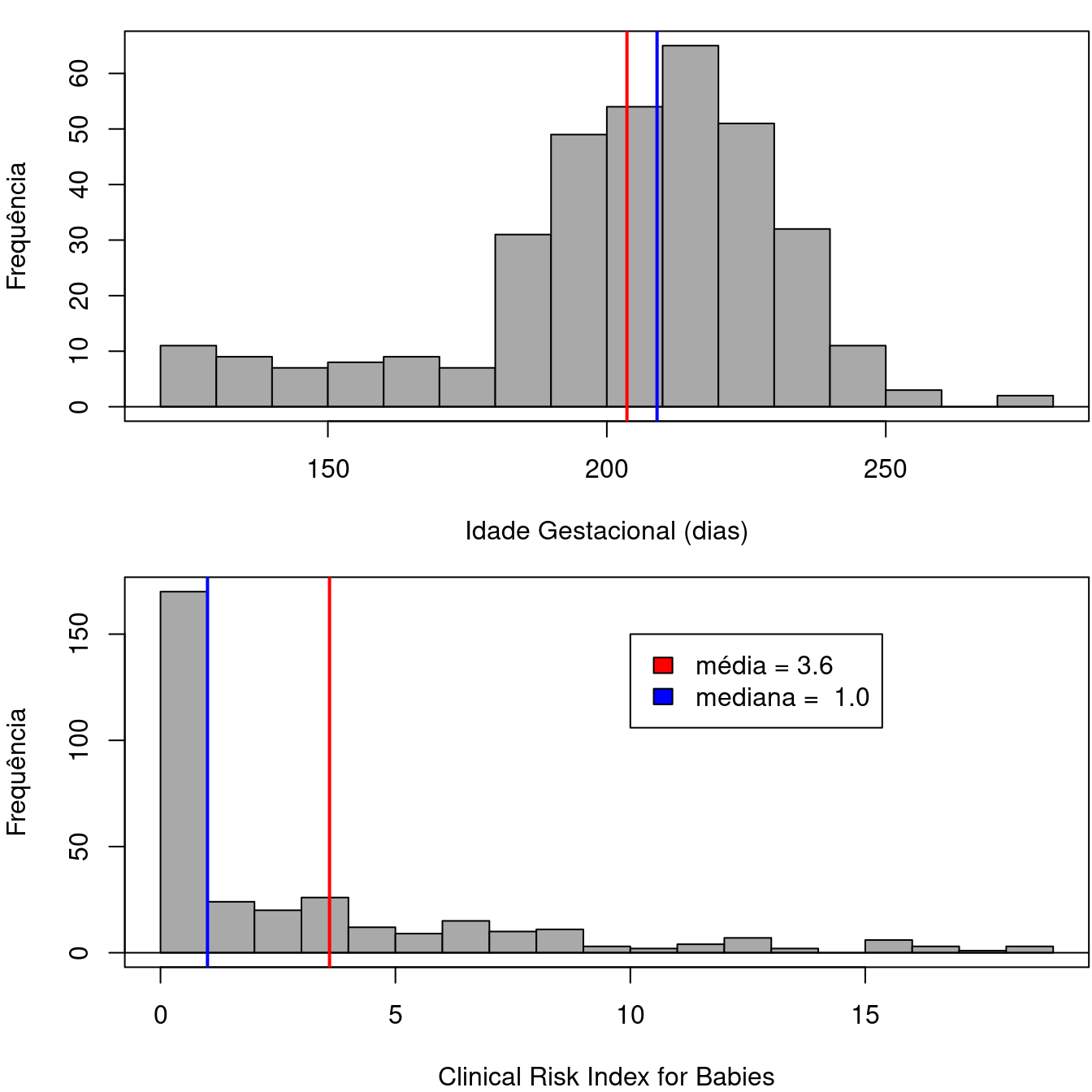
Figura 3.1: Exemplos de duas variáveis com distribuição assimétrica.

A figura 3.2 mostra o histograma da variável fração inspirada de O₂ máxima. Nesse caso, os valores parecem se concentrar em dois locais diferentes.

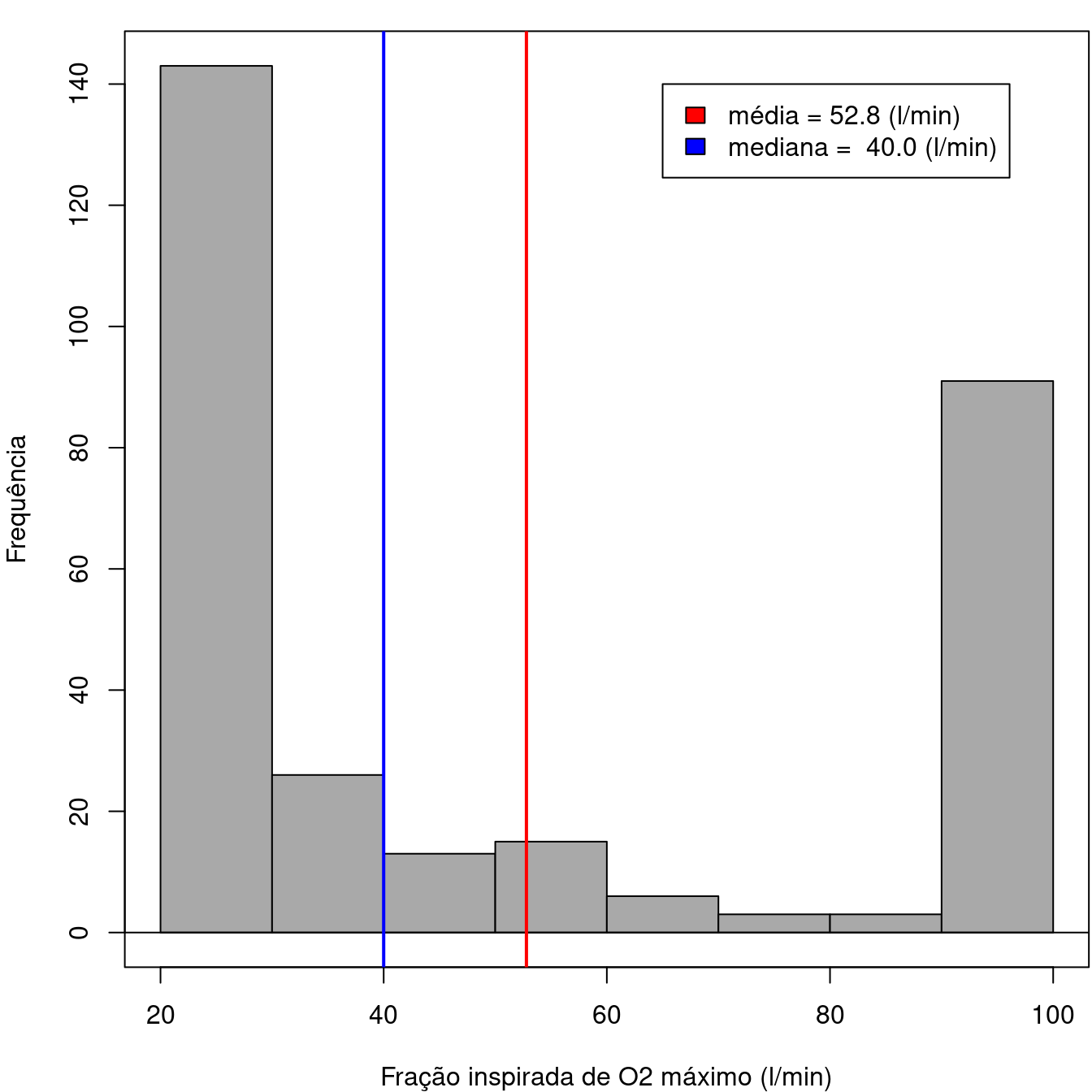
Figura 3.2: Exemplo de uma variável não distribuída em torno de um ponto central.

A figura 3.3 mostra a distribuição do peso ao nascimento para crianças que sobreviveram e as que foram a óbito. Pode-se observar, que a dispersão das duas distribuições são parecidas, mas o peso das crianças que sobrevivem tendem a ser maiores do que o peso das que vão a óbito. Ambas as distribuições são assimétricas, sendo uma para a direita e outra para a esquerda.

As medidas numéricas mais comuns utilizadas para resumir os dados são as medidas de tendência central, dispersão, simetria e curtose. Neste capítulo, serão apresentadas as principais medidas de tendência central e dispersão, que são as mais frequentes em relatórios e artigos científicos.

O primeiro conjunto de medidas numéricas caracteriza a tendência central ou ‘centro de massa’ dos dados ou distribuição. O segundo conjunto procura refletir o espalhamento dos dados em torno do centro; são as medidas de dispersão.

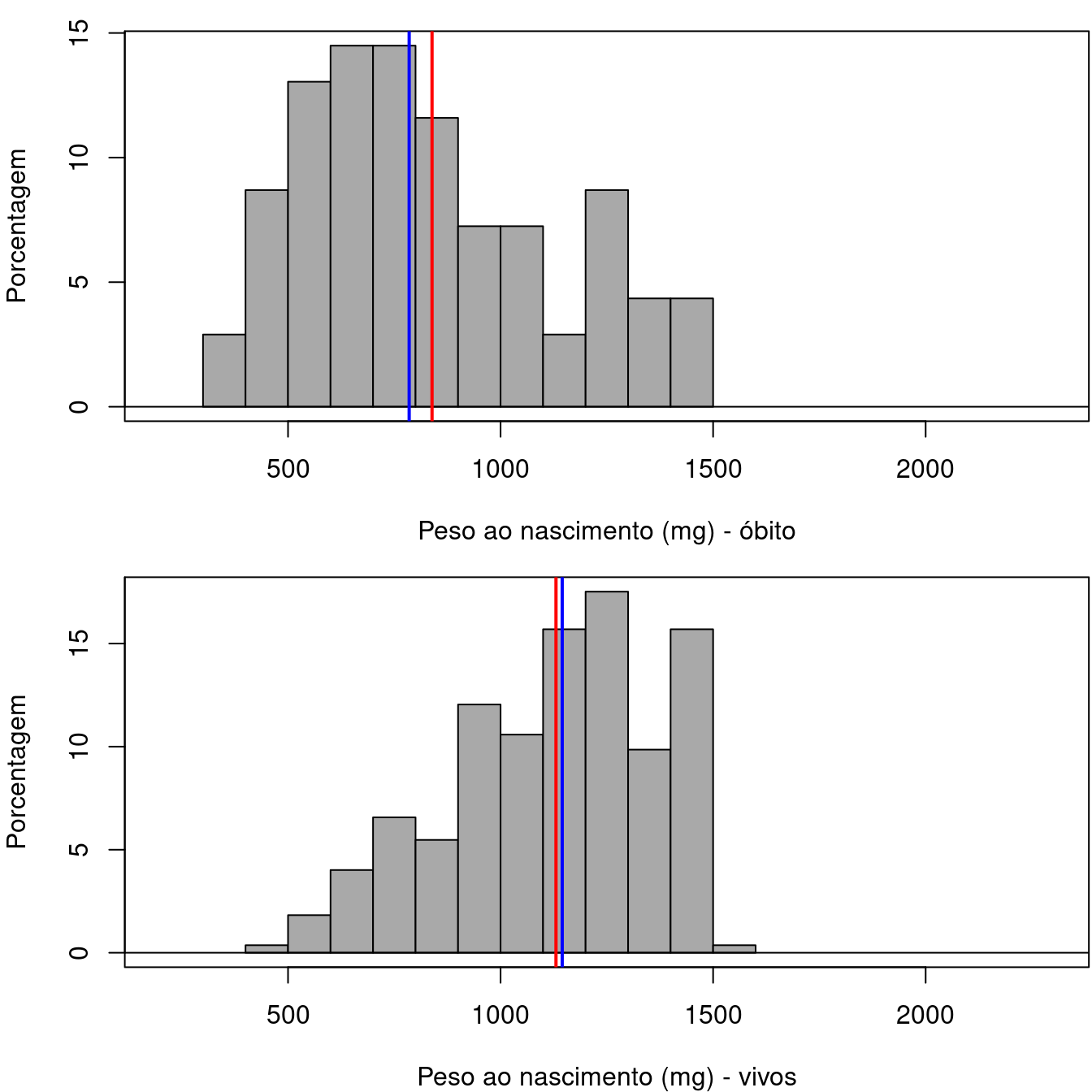
Figura 3.3: Variáveis com distribuições com medidas de tendência central diferentes.

3.2 Medidas de tendência central

As medidas de tendência central são aquelas que buscam refletir o ponto de equilíbrio dos dados. Não há uma única medida de tendência central, e a razão para isso será mostrada com exemplos.

Os conteúdos das subseções desta seção podem ser visualizados neste vídeo.

3.2.1 Média

A média, ou média aritmética (mean em inglês), é a mais conhecida, sendo de fácil obtenção. Assumindo que a variável x possua n valores x_i , i = 1, 2, …, n, a média aritmética é calculada por meio da expressão:

\[\bar{x} = \frac{\sum_{i=1}^{n}x_{i}}{n}\] Vamos considerar a variável x que contém 15 valores, criada por meio do comando abaixo. O sinal “<-” ou “=” significa que o resultado da operação à direita do sinal é atribuído ao objeto à esquerda do sinal. A função c cria um vetor com os elementos dentro dos parênteses, separados por vírgula.

x <- c(10, 9, 8, 12, 11, 7, 10, 8.5, 9.5, 6, 14, 13, 11, 12, 9)

Para obtermos a média de uma variável x no R, utilizamos a função mean:

mean(x)

## [1] 10

Nesse exemplo, a média dá uma boa ideia da tendência central dos dados, mas em outras situações ela pode ser enganosa. Um exemplo é a renda per capita média em um país com uma distribuição da renda bastante desigual, como o Brasil. Nesse caso, a renda média é bastante influenciada por indivíduos que possuem renda bem acima da maioria da população.

No exemplo da variável x acima, se substituirmos o primeiro valor de x por um que seja dez vezes a média, o que aconteceria com a média? Utilizando o R, podemos verificar como a média de x se altera.

O comando abaixo altera o primeiro valor de x para um valor igual a 10 vezes a média de x:

# substituindo o primeiro elemento de x por 10 vezes a média da variável
x[1] = 10*mean(x)

Vamos interpretar esse comando. Lembrem que a variável x contém os valores 10, 9, 8, 12, 11, 7, 10, 8.5, 9.5, 6, 14, 13, 11, 12 e 9. Cada valor da variável x pode ser acessado, bastando indicar a posição do valor (índice do valor) entre colchetes. Assim x[1] aponta para o primeiro elemento de x.

Então o comando x[1] = 10 * mean(x) atribui ao primeiro elemento de x o valor da média multiplicado (*) por 10. Na linha de comando do R, tudo que aparece após o sinal # é interpretado como comentário, apenas para esclarecer ao usuário a intenção do comando. Ele é ignorado pelo R.

Para visualizar o novo valor de x[1], execute o comando abaixo:

x[1]

## [1] 100

Agora, a nova média da variável x é:

mean(x)

## [1] 16

Assim um único valor bastante acima dos demais valores de uma variável deslocou a média para um valor acima de todos os outros valores da variável. Aqui temos um caso de valores extremos influenciando a média. Uma medida de tendência central que não é influenciada por valores extremos é a mediana.

3.2.2 Mediana

A mediana (median em inglês) é definida como o valor tal que 50% dos valores da variável estão acima da mediana e 50% estão abaixo. A obtenção da mediana é feita ordenando-se os dados e escolhendo-se o valor do meio. Por exemplo, se temos 21 valores, a mediana estará na 11^a posição. No caso de o número N de dados ser par, computamos a média dos dois valores ‘centrais’ (com 10 valores, a mediana será a média do 5^o e 6^o valor).

No R, temos a função median para fazer esse cálculo. Para a variável x, definida na seção anterior, o valor da mediana será obtido assim:

median(x)

## [1] 10

Observem que a mediana, mesmo com os dados tendo um valor 10 vezes maior que sua média, resulta em uma estimativa mais típica dos valores da variável x. A mediana é considerada uma medida robusta da tendência central, por não sofrer influências de valores extremos. Vamos verificar como a mediana foi calculada para a variável x. A função sort ordena a variável, conforme mostra a figura 3.4.

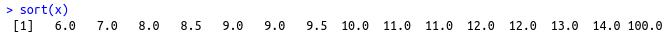
Figura 3.4: Ordenação dos valores da variável x em ordem crescente por meio do comando sort(x).

Como x possui 15 elementos, a mediana será o valor apontado pelo elemento na posição 8, depois que x foi ordenado. Esse valor é 10, como indicado pela seta azul na figura 3.5. O fato de o maior valor da variável ser 100, 1000 ou 10000000000 não terá nenhuma influência na determinação da mediana.

Figura 3.5: Posição da mediana da variável x indicada pela seta azul.

Assim, para dados que são assimétricos, a mediana é um melhor representante de um valor típico dos dados.

3.2.3 Moda

Considere a seguinte variável y que pode representar, por exemplo, a idade de pessoas que fazem parte de um grupo de pais que ensinam os seus filhos bem novos a nadar:

y = c(1, 1, 1, 2, 2, 2, 2, 3, 3, 31, 31, 32, 32, 32, 32, 33, 33, 33)
y

##  [1]  1  1  1  2  2  2  2  3  3 31 31 32 32 32 32 33 33 33

median(y)

## [1] 17

mean(y)

## [1] 17

A média e a mediana de y não refletem o valor típico de y, que contém idades de crianças bem pequenas e dos respectivos pais. Essa variável possui mais de um valor típico: um para as crianças e outro para os pais. Uma medida que pode ser usada nesses casos é a moda.

A moda é a medida de maior frequência em um conjunto de dados. Os passos para se obter a moda são:
1) encontrar todos os valores distintos da variável;
2) obter a frequência de cada valor distinto;
3) selecionar o valor (ou valores) com a maior frequência para obter a moda.

Seguindo esses passos para o exemplo acima, temos:

valores distintos: 1, 2, 3, 31, 32, 33
frequências:
1 → 3
2 → 4
3 → 2
31 → 2
32 → 4
33 → 3
os dois valores com a maior frequência são 2 e 32. Assim a variável y possui duas modas.

Essa variável é bimodal.

Como obter a moda no R? O R não possui uma função específica para obtenção da moda, entretanto podemos usar uma composição de funções e métodos de indexação para obtermos esse valor. Uma possibilidade é usar os seguintes comandos:

temp <- table(y)    # a função table gera uma tabela de frequências
                    # para a variável y
temp

## y
##  1  2  3 31 32 33 
##  3  4  2  2  4  3

Armazenamos a tabela de frequências de y, gerada a partir da função table em temp. Ao visualizarmos o conteúdo de temp, vemos a tabela de frequência igual à que calculamos manualmente. Na primeira linha aparece os elementos distintos de y e na linha abaixo as frequências de cada valor. Agora basta pegar os valores com contagem máxima, usando o comando a seguir:

names(temp)[temp == max(temp)]

## [1] "2"  "32"

Os valores obtidos para a moda foram 2 e 32, os mesmos obtidos manualmente. Vamos entender o comando acima. A função names(temp) retorna os valores distintos da variável y, ou a primeira linha da tabela temp:

names(temp)

## [1] "1"  "2"  "3"  "31" "32" "33"

A função max(temp) retorna a frequência máxima da tabela temp (4 nesse exemplo):

max(temp)

## [1] 4

A expressão temp == max(temp) vai retornar todos os itens de temp cujas contagens sejam iguais à frequência máxima. Logo temp[temp == max(temp)] retorna os elementos da tabela de frequência com frequência máxima:

temp[temp == max(temp)]

## y
##  2 32 
##  4  4

Finalmente names(temp)[temp == max(temp)] retorna os valores com frequência máxima.

Mesmo que, ao aplicarmos o processo acima, identifiquemos um único valor que possua a frequência máxima, pode acontecer que, ao inspecionarmos o histograma da variável, identificamos que a distribuição dos dados parece se concentrar em mais de um ponto, por exemplo a distribuição da variável fiO2_maximo (figura 3.2). Nesses casos, dizemos que a função possui mais de uma moda, porque existe mais de um local onde os valores parecem se concentrar. No exemplo do fiO2_maximo, diríamos que a variável é bimodal.

3.2.4 Discussão sobre medidas de tendência central

Que medida de tendência central deve ser usada ou apresentada em relatório ou artigo científico?

Depende dos dados! Como vimos nos exemplos acima, podem ocorrer diversas situações:

os dados estão distribuídos simetricamente em torno de um ponto central;
existem valores no conjunto de dados que se desviam marcadamente dos valores típicos (conhecidos em inglês por “outliers”);
as variáveis podem estar distribuídas de maneira assimétrica em maior ou menor grau;
os dados podem estar distribuídos em torno de mais de um valor;
etc.

No primeiro caso acima, a média é uma medida adequada. Já no terceiro caso, e às vezes no segundo, a mediana seria mais apropriada e, finalmente, no quarto caso, a moda seria a medida escolhida.

Assim o primeiro passo é inspecionar os dados e obter não somente as medidas de tendência central, como também conhecer como os dados estão dispersos em torno destas medidas, ou seja, precisamos também trabalhar com as medidas de dispersão, tema da seção seguinte.

3.3 Medidas de dispersão

Medidas de tendência central ou localização dos dados não dão a visão completa dos mesmos. Para melhor interpretarmos os dados, também necessitamos saber como estes estão ‘espalhados’, isto é, se os dados estão localizados em sua maioria em torno da medida de tendência central ou estão mais dispersos.

3.3.1 Amplitude

O conteúdo desta seção pode ser visualizado neste vídeo.

Suponhamos que, em um curso de estatística, tenhamos 12 alunos que obtiveram as seguintes notas finais: 50, 66, 72, 76, 78, 84, 85, 86, 88, 89, 92, 100. Para uma segunda turma, também de 12 alunos, as notas foram: 50, 78, 78, 80, 80, 83, 84, 84, 83, 83, 83, 100. No R, podemos entrar estes dados e produzir uma representação gráfica que irá refletir a distribuição das notas de cada turma.

x1 = c(50, 66, 72, 76, 78, 84, 85, 86, 88, 89, 92, 100)
x2 = c(50, 78, 78, 80, 80, 83, 84, 84, 83, 83, 83, 100)
mean(x1); mean(x2)

## [1] 80.5

## [1] 80.5

Os dois primeiros comandos criaram duas variáveis, cada uma com as notas de estatística de cada turma. O terceiro comando calculou as médias de cada turma que, coincidentemente, são iguais. Observem que, numa única linha de comando, foram executados duas funções de cálculo de médias, separadas por “;”. No R, o sinal “;” representa um separador de comandos.

Uma medida de dispersão simples é a amplitude (range em inglês), que é a distância entre o maior e o menor valor do conjunto de dados. Usualmente, ela é calculada por max(X) - min(X), onde X é a variável de interesse. A função range no R fornece o menor e o maior valor da variável entre parênteses:

range(x1); range(x2)

## [1]  50 100

## [1]  50 100

A partir da função range, a amplitude de cada uma das variáveis poderia ser obtida, subtraindo-se o primeiro valor do segundo valor gerado pela função range. A função diff calcula essa diferença. Podemos ver que a amplitude é a mesma para as variáveis x1 e x2.

diff(range(x1))

## [1] 50

diff(range(x2))

## [1] 50

Vamos ver uma representação gráfica simples para esses dados. Os três comandos abaixo criam dois gráficos para variáveis discretas, o primeiro para a variável x1 e o segundo para a variável x2 (figura 3.6).

library(RcmdrMisc)
par(mar = c(4, 4, 1, 1), mfcol=c(1, 2))
discretePlot(x1, scale="frequency", ylab = "Frequência")
discretePlot(x2, scale="frequency", ylab = "Frequência")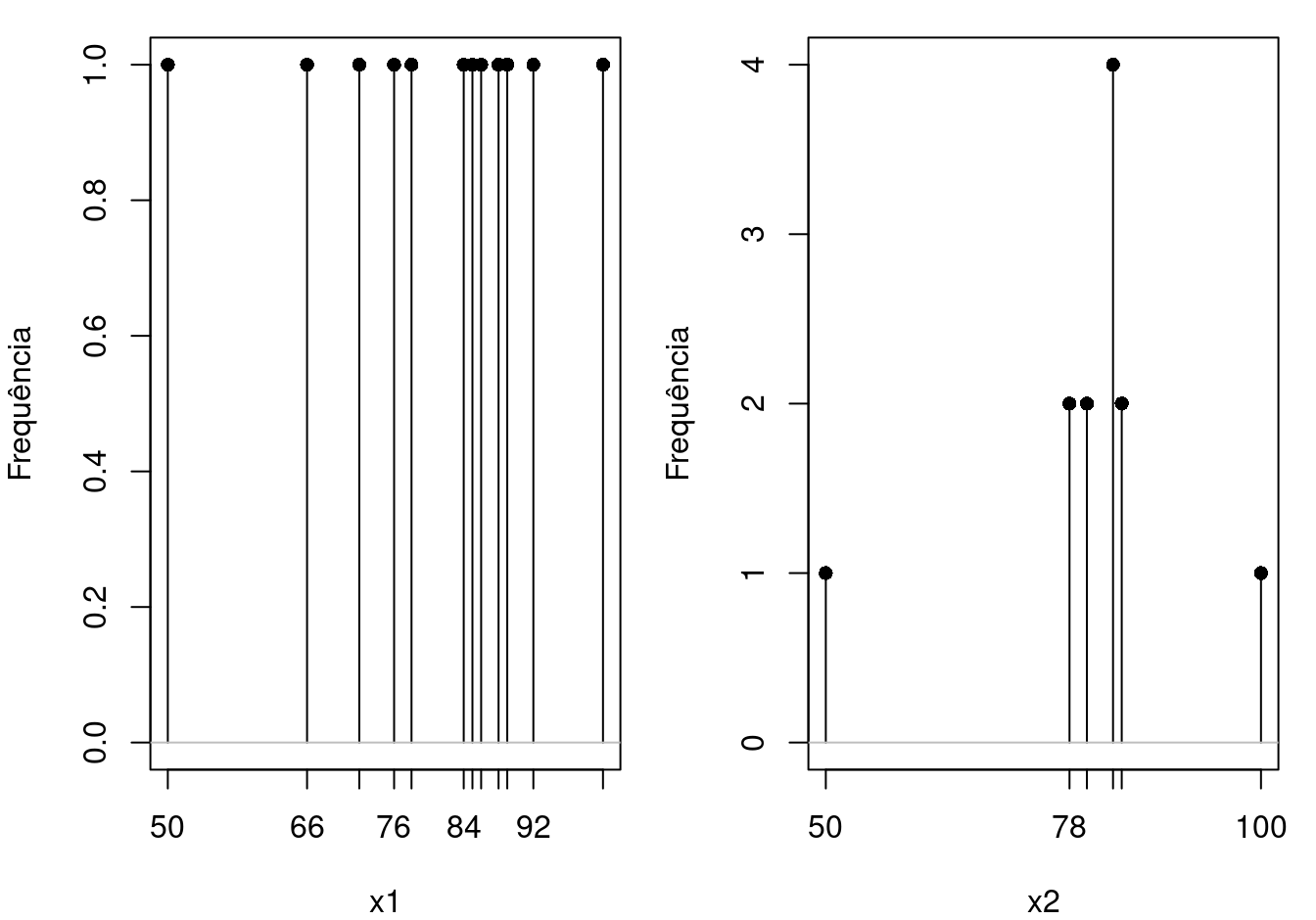

Figura 3.6: Gráfico de barras para as variáveis x1 e x2.

Observem que as distribuições têm diferentes formas, a mesma média e também a mesma amplitude, mas os valores da variável x1 estão mais espalhados do que os da variável x2. Devemos notar que a amplitude só considera os valores extremos, portanto não dá uma boa descrição da distribuição dos dados. Há muitas formas diferentes de construir variáveis com a mesma amplitude, mas diferentes distribuições dos valores. Uma vez que a amplitude considera os valores mais extremos de um conjunto de dados, ela não permite saber como eles estão distribuídos, ou se existem outliers. Precisamos de outras medidas de dispersão.

3.3.2 Distância interquartil

Os conteúdos desta seção e da seção 3.3.3 podem ser visualizados neste vídeo.

Uma medida de dispersão que não sofre a influência de valores extremos é a amplitude interquartil, ou distância interquartil (DIQ ou IQR - Interquatile range, em inglês). Antes vamos apresentar o conceito de quantil.

Os quantis dividem os valores ordenados de uma variável numérica em q partes essencialmente iguais, ou em q partes com a mesma proporção de valores. Essa divisão dá origem a q-quantis.

Alguns quantis têm nomes especiais:
• Os 100-quantis são chamados percentis
• Os 10-quantis são chamados decis
• Os 5-quantis são chamados quintis
• Os 4-quantis são chamados quartis
• Os 3-quantis são chamados tercis

Podemos intepretar os quantis como medidas de posição. Diversas medidas de dispersão podem ser definidas a partir de quantis. Possivelmente, a mais utilizada delas é a distância interquartil.

Para entendermos a distância interquartil, precisamos inicialmente definir os quartis. Quartis são quantis que dividem os valores da variável em quatro partes:
1) Q1 (primeiro quartil, ou quartil inferior) define o valor para o qual 25% dos valores estão abaixo dele;
2) Q2 (segundo quartil) é o valor que tem 50% dos valores abaixo e 50% acima (é a mediana);
3) Q3 (terceiro quartil ou quartil superior) define o valor que possui 75% dos dados abaixo dele.

O intervalo interquartil é a amplitude (distância) entre o primeiro e terceiro quartil

IQR = Q3 ‑ Q1

Há diversos algoritmos para o cálculo dos quartis. Assim, dependendo do algoritmo, valores ligeiramente diferentes poderão ser obtidos, tanto para os quartis quanto para a distância interquartil. Um algoritmo simples funciona como a seguir.

Determinando o primeiro quartil:
1. ordene os valores em ordem crescente;
2. seja n o número de valores. Divida n por 4 (obter 25% de n);
3. se essa divisão for um número inteiro, então o primeiro quartil é o valor obtido pela média aritmética entre o valor na posição indicada por essa divisão e o valor seguinte;
4. se a divisão não for inteira, arredonde o número para cima. Esse número dá a posição do primeiro quartil.

Vamos aplicar esse algoritmo à variável x1 no exemplo da seção anterior. Temos 12 elementos, logo 12/4 = 3. O número na posição 3 é 72, como mostra a seta azul na figura 3.7.

Figura 3.7: Posição indicada pela seta azul para o cálculo do primeiro quartil da variável x1.

Assim o primeiro quartil de x1 é a média aritmética entre 72 e o valor na posição seguinte (76). Logo:

Q1 = (72 + 76) / 2 = 74

Determinando o terceiro quartil:
1. Ordene os valores em ordem crescente;
2. seja n o número de valores. Divida 3n por 4 (obter 75% de n);
3. se essa divisão for um número inteiro, então o terceiro quartil é o valor obtido pela média aritmética entre o valor na posição indicada por essa divisão e o valor seguinte;
4. se a divisão não for inteira, arredonde o número para cima. Esse número dá a posição do terceiro quartil.

Vamos aplicar esse algoritmo à variável x1 no exemplo da seção anterior. Temos 12 elementos, logo (3 x 12)/4 = 9. O número na posição 9 é 88, como mostra a seta na figura 3.8.

Figura 3.8: Posição indicada pela seta azul para o cálculo do terceiro quartil da variável x1.

Assim o terceiro quartil de x1 é a média artimética entre 88 e o valor na posição seguinte (89). Logo:

Q3 = (88 + 89) / 2 = 88,5

A distância interquartil para a variável x1 é Q3 – Q1 = 14,5 (88,5 – 74). Para obtermos os quartis no R (ou qualquer quantil), usamos a função quantile. Para obtermos o primeiro quartil de x1, usamos a função quantile conforme mostrado a seguir:

quantile(x1, 0.25, type=2)

## 25% 
##  74

Para obtermos o terceiro quartil de x1, usamos a função quantile conforme mostrado a seguir:

quantile(x1, 0.75, type=2)

##  75% 
## 88.5

A função quantile admite 9 diferentes algoritmos, especificado pelo argumento type. Fazendo type = 2, será utilizado o algoritmo explicado acima.

Podemos obter o primeiro e o terceiro quartil com uma única chamada da função, da seguinte forma:

quantile(x1, probs = c(0.25, 0.75), type=2)

##  25%  75% 
## 74.0 88.5

Para a variável x2, os valores do primeiro e do terceiro quartil serão:

quantile(x2, probs = c(0.25, 0.75), type=2)

##  25%  75% 
## 79.0 83.5

A função IQR fornece a distância interquartil. Obtendo a distância interquartil de x1:

IQR(x1, type=2)

## [1] 14.5

Obtendo a distância interquartil de x2:

IQR(x2, type=2)

## [1] 4.5

A variável x2 possui uma dispersão menor do que a variável x1, quando utilizamos a distância interquartil, refletindo melhor a distribuição das variáveis x1 e x2.

A distância interquartil é uma medida de variabilidade mais estável ou ‘robusta’, pois ela não é influenciada por valores extremos, como é o caso da amplitude.

3.3.3 Percentis

Os percentis são quantis utilizados com bastante frequência. O percentil 10, indicado por P₁₀, designa o valor para o qual 10% dos valores da variável estão abaixo dele e assim por diante.

O primeiro quartil (Q1) é, portanto, igual ao P₂₅; a mediana é igual ao P₅₀, e o terceiro quartil (Q3) é igual ao P₇₅. Um algoritmo semelhante ao utilizado para o cálculo do quartil pode ser utilizado para os percentis.

Assim para calcular o percentil $\alpha$%:
a) ordene os valores em ordem crescente;
b) seja n o número de valores. Multiplique n por $\alpha$/100;
c) se essa divisão for um número inteiro, então P_$\alpha$ é o valor obtido pela média aritmética entre o valor na posição indicada por essa divisão e o valor seguinte;
d) se a divisão não for inteira, arredonde o número para cima. Esse número dá a posição de P_$\alpha$.

Vamos calcular o P₁₀ para a variável x1 no exemplo da seção anterior. Temos 12 elementos, logo 12 x 10/100 = 1,2. Como essa divisão não é inteira, arredondamos o quociente para cima. Essa é a posição do P₁₀ (seta azul na figura 3.9). Logo P₁₀ = 66.

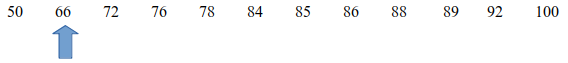
Figura 3.9: Posição indicada pela seta azul para o cálculo do percentil 10 da variável x1.

No R, para obtermos qualquer percentil, usamos a função quantile com o valor do percentual desejado. Logo, para obtermos o P₁₀ de x1, fazemos:

quantile(x1, 0.10, type=2)

## 10% 
##  66

Um exemplo da utilização de percentis são as curvas de crescimento, utilizadas para comparar o desenvolvimento de uma criança, por exemplo, com o crescimento esperado de uma população de crianças. A figura 3.10 mostra as curvas de crescimento (peso por idade) para meninas do nascimento até 5 anos, padronizadas pela Organização Mundial de Saúde (OMS). As curvas indicam, de baixo para cima, os percentis 3%, 15%, 50%, 85% e 97%, respectivamente. Na idade de 3 anos, por exemplo, a curva do percentil 3% indica que 3% das crianças pesam menos de 11 Kg (indicado pela seta vermelha na figura).

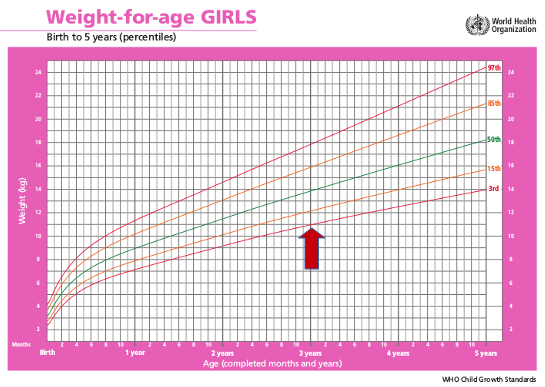
Curvas de crescimento padronizadas pela OMS. A seta indica o P3 do peso para a idade de 3 anos. Fonte: Organização Mundial de Saúde (CC BY-NC-SA 3.0 IGO).

Figura 3.10: Curvas de crescimento padronizadas pela OMS. A seta indica o P₃ do peso para a idade de 3 anos. Fonte: Organização Mundial de Saúde (CC BY-NC-SA 3.0 IGO).

3.3.4 Desvio padrão e variância

Os conteúdos desta seção e da seção 3.3.5 podem ser visualizados neste vídeo.

Um problema com as medidas de dispersão anteriores, como a amplitude e a distância interquartil, é que elas mostram somente as diferenças entre valores em determinadas posições, quando se ordenam os valores da variável. Existe alguma medida que indica a variabilidade de uma variável, mas que leva em conta todos os seus valores?

Sim. Uma primeira ideia é calcular o desvio de cada valor em relação à média $\begin{aligned} (x - \bar{x}) \end{aligned}$, somá-los e dividir o resultado pelo número de valores. O problema é que o desvio médio será sempre 0. Desvios negativos serão cancelados por desvios na outra direção, como mostra a expressão abaixo:
\[\frac{1}{n} \sum_{i=1}^{n}(x_{i}-\bar{x})=\frac{1}{n} \left(\sum_{i=1}^{n}x_{i}-\sum_{i=1}^{n}\bar{x}\right) =\frac{1}{n} \sum_{i=1}^{n}x_{i}-\frac{1}{n}\sum_{i=1}^{n}\bar{x}=\bar{x}-\bar{x}=0\]

Uma segunda possibilidade é calcular a média das distâncias de cada valor à média. A distância de cada valor à média é sempre positiva. Se o valor está acima da média, a distância é igual ao desvio. Se o valor estiver abaixo da média, a distância é igual ao oposto do desvio.

Uma outra alternativa é elevar cada desvio em relação à média ao quadrado, somá-los e dividir essa soma por n-1. Nesse caso, todas as parcelas da soma serão positivas e a medida de variabilidade assim obtida é chamada de variância (s²).

\[s^2 = \frac{1}{n-1} \sum_{i=1}^{n}(x_{i}-\bar{x})^2\]

A razão por que divide-se por n-1 e não por n será vista no capítulo sobre propriedades de estimadores (capítulo 13).

O desvio padrão (s) é calculado, extraindo-se a raiz quadrada da variância s², e é medido na mesma unidade da variável à qual ele se refere. \[s = \sqrt{s^2}\] O desvio padrão e a variância consideram todos os valores da variável para o seu cálculo e são bastante utilizados na análise estatística.

No R, temos como obter essas medidas, usando a função sd para o desvio padrão ou var para a variância.

var(x1); var(x2)

## [1] 176.6364

## [1] 124.8182

sd(x1); sd(x2)

## [1] 13.29046

## [1] 11.17221

Como nas medidas de distância interquartil, os desvios padrões de x1 e x2 também indicam uma maior dispersão para x1.

3.3.5 Discussão sobre as medidas de dispersão

Diversas medidas de dispersão foram apresentadas nas seções anteriores. A amplitude é uma medida bastante simplista de dispersão, já que ela mede a distância entre o maior e o menor valor, mas não fornece nenhuma indicação de como os valores estão distribuídos em torno de uma medida de tendência central, como a média e a mediana.

A variância e o desvio padrão são medidas bem mais adequadas para indicar a variabilidade dos dados e como eles estão dispersos, já que elas consideram como os dados estão agrupados.

Há uma conexão entre a média, o desvio padrão e amplitude. Se X for uma variável, n o número de valores, m a média aritmética e s o desvio padrão, Harding (Harding 1996) mostrou que:

\[m-s \sqrt{n-1} \leq X \leq m + s \sqrt{n-1}\]

Logo a amplitude é, no máximo, $2s \sqrt{n-1}$

A apresentação do 1^o, 2^o (Mediana) e 3^o quartis dá uma boa noção da dispersão dos dados e também indica se os dados estão distribuídos simetricamente em torno da mediana. Essas medidas são as mais frequentemente utilizadas para a construção dos diagramas de caixa (boxplot em inglês), que serão apresentados no próximo capítulo.

Para variáveis que seguem um distribuição normal (em forma de sino), o desvio padrão tem uma interpretação simples: 68,3% dos valores da variável estão situados a uma distância de um desvio padrão em torno da média aritmética (figura 3.11). Essa figura superpõe uma curva normal em um histograma com forma de sino. A distribuição normal será apresentada no capítulo 11.

Entretanto, para outras distribuições, a interpretação pode ser diferente. A figura 3.12 mostra quatro distribuições diferentes, todas com o mesmo valor do desvio padrão, mas que a probabilidade de selecionarmos aleatoriamente um valor da variável e ele estar na região compreendida entre a média $\pm$ desvio padrão varia de uma distribuição para outra. A distribuição indicada pela letra d é assimétrica em relação à média, ou seja, há uma probabilidade maior de se obter aleatoriamente valores abaixo da média do que acima dela; nesse caso, a mediana e os percentis P₂₅ e P₇₅ são melhores medidas de tendência central e dispersão do que a média e o desvio padrão.

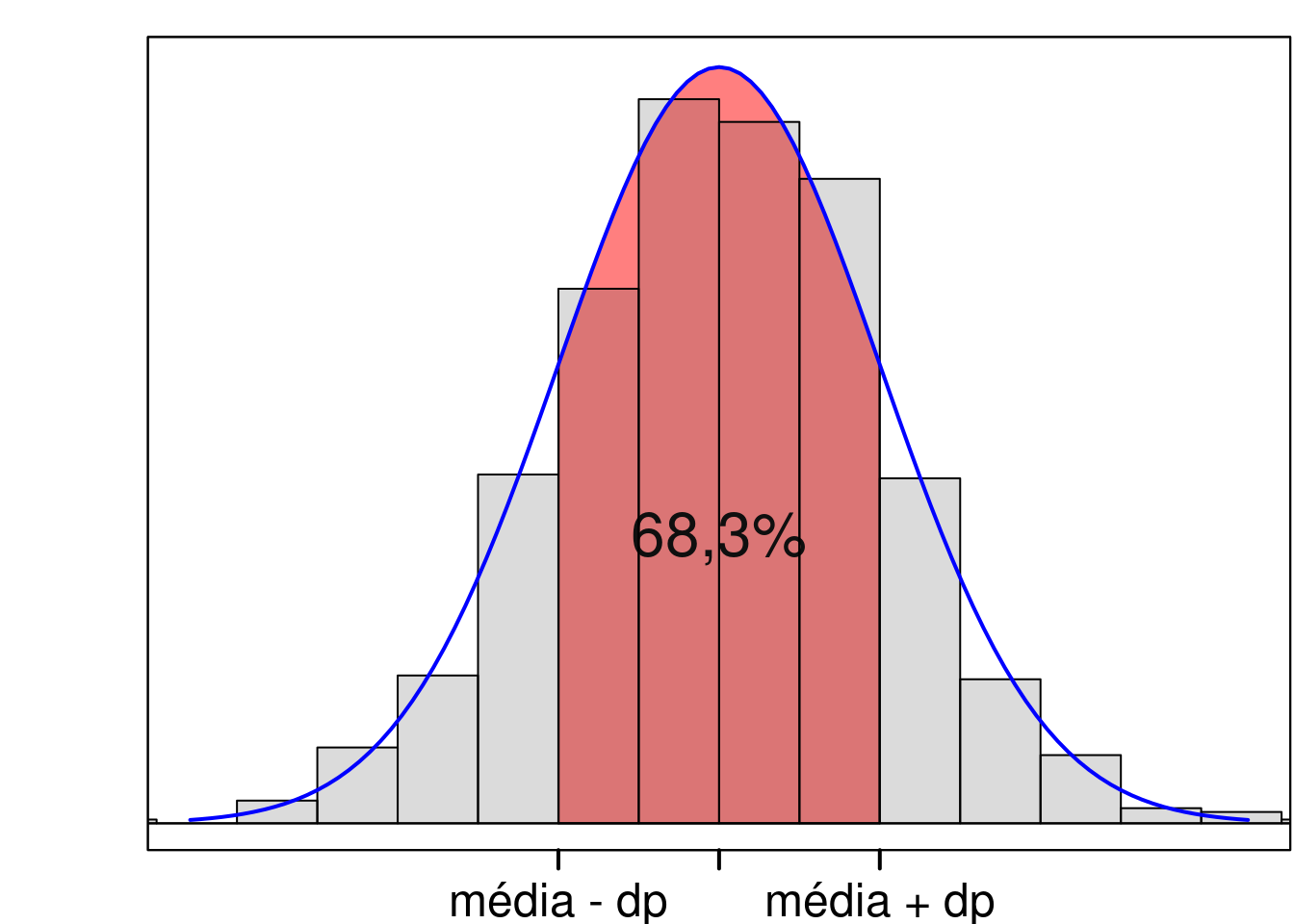
$Em variáveis que seguem uma distribuição normal, 68,3\% dos valores da variável estão situados a uma distância de um desvio padrão em torno da média aritmética.$

Figura 3.11: Em variáveis que seguem uma distribuição normal, 68,3% dos valores da variável estão situados a uma distância de um desvio padrão em torno da média aritmética.

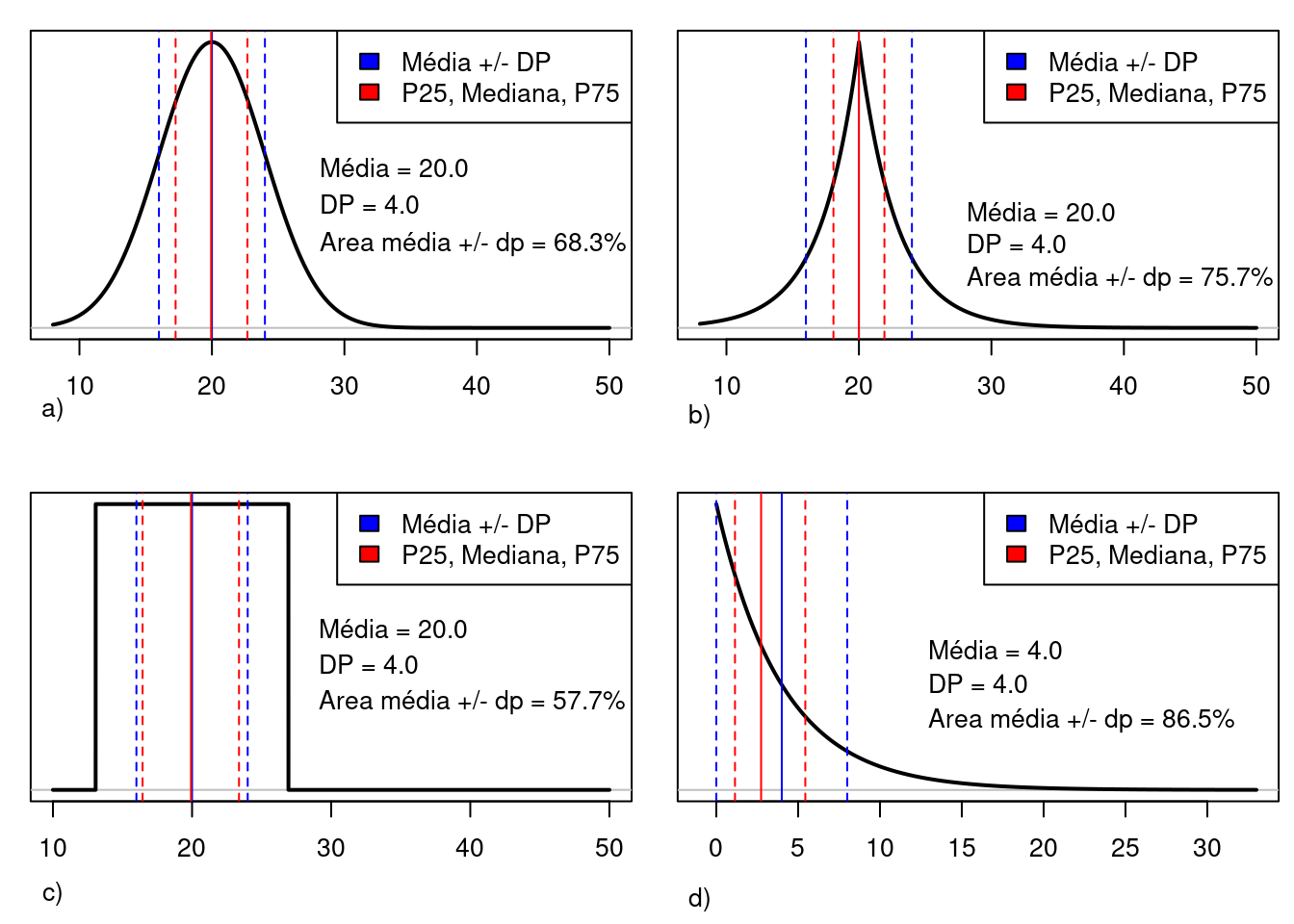
$Diferentes distribuições de dados que mostram diferentes probabilidades de os valores se situarem na região compreendida entre a média $\pm$ desvio padrão. Quando a distribuição é assimétrica (d), a mediana e os percentis P25 e P75 dos dados são melhores medidas de tendência central e dispersão.$

Figura 3.12: Diferentes distribuições de dados que mostram diferentes probabilidades de os valores se situarem na região compreendida entre a média $\pm$ desvio padrão. Quando a distribuição é assimétrica (d), a mediana e os percentis P₂₅ e P₇₅ dos dados são melhores medidas de tendência central e dispersão.

A figura 3.13 mostra uma distribuição empírica onde os dados se concentram em duas regiões distintas. Nesse exemplo, nem a mediana, P₂₅ e P₇₅ e a média e desvio padrão são boas medidas de tendência central e dispersão. É melhor caracterizar essa distribuição como bimodal.

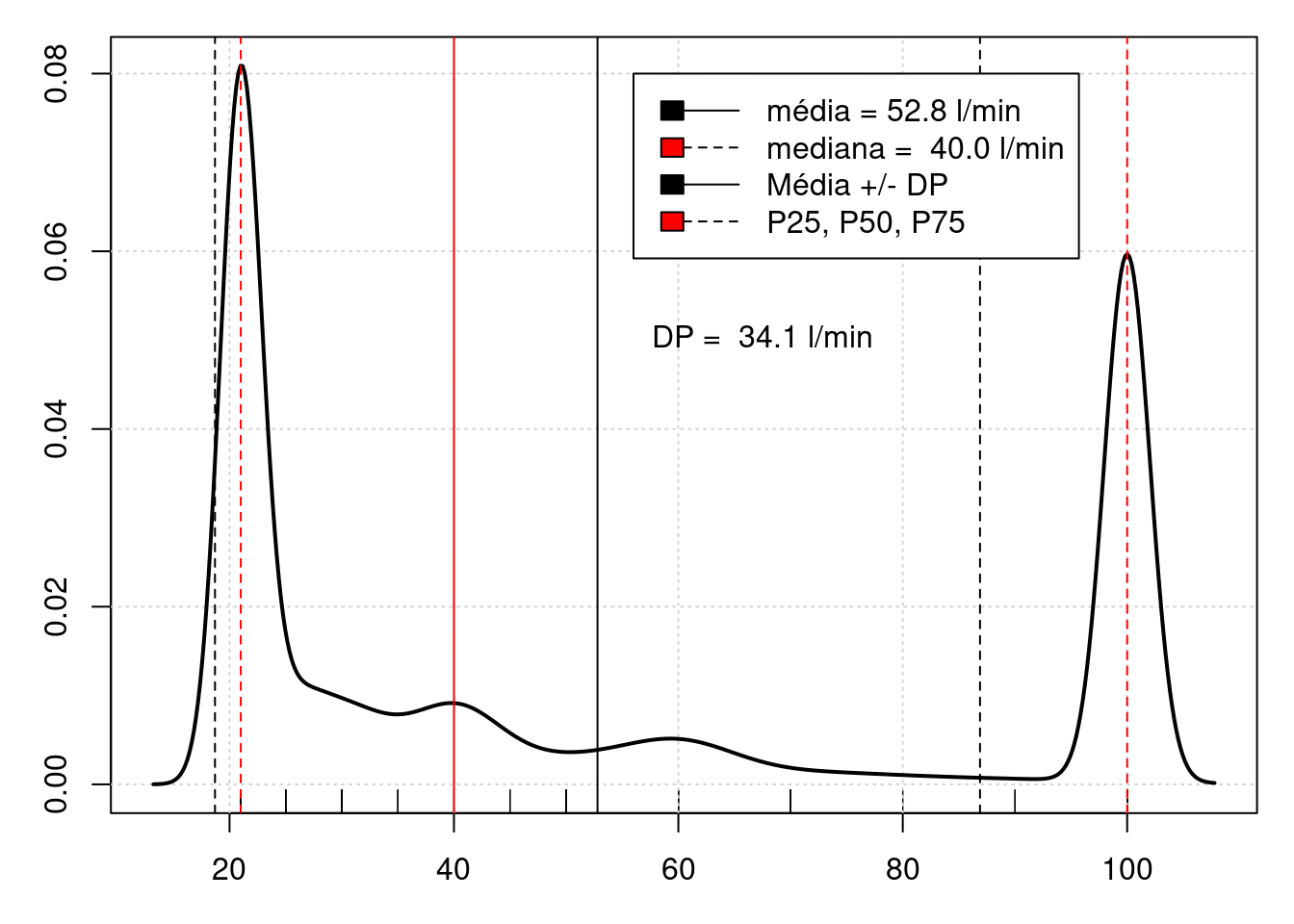
Figura 3.13: Distribuição bimodal.

O R tem uma função, summary, que fornece de uma única vez várias estatísticas descritivas discutidas aqui. Vamos utilizá-la para os valores de x2.

summary(x2)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   50.00   79.50   83.00   80.50   83.25  100.00

A função summary fornece o valor mínimo, o valor máximo, a média, a mediana, o primeiro e o terceiro quartil. Observem que os valores do primeiro e do terceiro quartil são ligeiramente diferentes daqueles que calculamos anteriormente. Isso acontece porque, na chamada da função summary, se não especificarmos o tipo de algoritmo, é utilizado por padrão um algoritmo diferente do que utilizamos para calcular os quartis.

3.4 Apresentação das estatísticas descritivas em publicações

Os conteúdos desta seção e de suas subseções podem ser visualizados neste vídeo.

Os relatórios e artigos científicos de estudos clínico-epidemiológicos geralmente apresentam as medidas de tendência central e dispersão de variáveis numéricas. A seguir, serão mostrados exemplos de apresentações inadequadas e adequadas dessas medidas.

3.4.1 Exemplos de formas inadequadas de apresentação da média e desvio padrão

A frase a seguir foi extraída de um parágrafo de um trabalho científico: “Foram avaliados 33 pacientes. A idade variou de 32 a 74 anos (média: 51,4 $\pm$ 10,5).”

Inicialmente, os autores apresentam a amplitude da idade (32 a 74 anos). O que significa a expressão entre parênteses: (média: 51,4 $\pm$ 10,5)? Se somarmos 51,4 com 10,5, o valor não é igual a 74, o valor máximo de idade. Também se subtrairmos 10,5 de 51,4, o valor não é igual a 32, o mínimo de idade. Possivelmente, os autores querem dizer que o valor 10,5 é o desvio padrão da idade. Não seria mais claro para os leitores se os autores simplesmente escrevessem que o desvio padrão é 10,5?

O vício apresentado acima é bastante frequente. A tabela 3.1 mostra um exemplo de como a média e o desvio padrão são frequentemente apresentados. O problema dessa forma de apresentação é que induz a uma interpretação equivocada do desvio padrão. O desvio padrão é uma medida da dispersão dos dados, não da faixa de variação em torno da média.

Tabela 3.1: Exemplo de uma apresentação inadequada da média e da dispersão de uma variável.
Variável	Média ± DP
Idade (anos)	56,4 ± 5,1
Glicemia de jejum (mg/dl)	90,2 ± 21,4

A tabela 3.2 mostra outro exemplo que coloca o desvio padrão entre parênteses após a média, que seria uma forma adequada, porém coloca o desvio padrão precedido do sinal $\pm$. O que os autores querem dizer com o sinal $\pm$ antes do desvio padrão?

Tabela 3.2: Outro exemplo de uma apresentação inadequada da média e da dispersão de uma variável.
Variável	Média (DP)
Idade (anos)	56,4 (±5,1)
Glicemia de jejum (mg/dl)	90,2 (±21,4)

A sentença a seguir também foi extraída de um estudo: “Os dados foram apresentados como médias $\pm$ desvios-padrão (DP), mediana e variação, de acordo com a distribuição de normalidade.” A que se refere a palavra variação? Ao desvio padrão, distância interquartil, ou amplitude? Os autores não esclarecem.

A tabela 3.3 mostra uma tabela com o mesmo problema do texto acima.

Tabela 3.3: Exemplo de uma apresentação inadequada da média e da dispersão de uma variável.
Variável	Mediana (Variação)
Estatura (m2)	1,60 (1,5 - 1,7)
Massa corporal (kg)	52,7 (44,8-60,8)

3.4.2 Exemplos de formas adequadas de apresentação da média, mediana, desvio padrão e primeiro e terceiro quartis

A tabela 3.4 mostra um exemplo que segue a boa prática para a apresentação da média e do desvio padrão: média seguida do desvio padrão entre parênteses.

Tabela 3.4: Exemplo de uma apresentação adequada da média e da dispersão de uma variável.
Variável	Média (DP)
Idade (anos)	56,4 (5,1)
Glicemia de jejum (mg/dl)	90,2 (21,4)

A tabela 3.5 mostra uma tabela que mostra a mediana e entre parênteses os valores do primeiro e terceiro quartil, que é uma forma clara e não ambígua de mostrar a dispersão de uma variável.

Tabela 3.5: Exemplo de uma apresentação adequada da mediana e da dispersão de uma variável.
Variável	Mediana (1^o quartil - 3^o quartil)
Estatura (m2)	1,60 (1,5 - 1,7)
Massa corporal (kg)	52,7 (44,8-60,8)

3.5 Escore z ou Escore padrão

Vamos considerar o seguinte exemplo, extraído do livro “Head First Statistics” (Griffiths 2008). Dois jogadores de um time de basquetebol, com diferentes habilidades, possuem os seguintes desempenhos:
Jogador 1: acerta 70% das cestas com um desvio padrão de 20%.
Jogador 2: acerta 40% das cestas com um desvio padrão de 10%.

Em um certo jogo, o jogador 1 teve 75% de acertos e o jogador 2, 60%. Qual jogador teve o melhor desempenho, levando em conta o seu desempenho histórico?

O jogador 1 acertou um maior percentual de cestas do que o jogador 2, mas isso era esperado em função de seu retrospecto. Entretanto, se levarmos em conta a média e o desvio padrão de cada jogador, verificamos que o jogador 2 teve uma atuação marcante nesse jogo: ele acertou 20% a mais do que o esperado (60% - 40%), 2 desvios padrões (2 x 10%) a mais do que a sua média.

O jogador 1 acertou apenas 5% a mais do que a sua média (75% - 70%), um quarto do desvio padrão (0,25 x 20%) acima de sua média.

Olhando por essa perspectiva, o jogador 2 teve o melhor desempenho, quando comparado com o seu desempenho normal. Essa medida que foi utilizada para a comparação é chamada escore z (z-score em inglês) ou escore padrão e é obtida pela fórmula: \[z = \frac{x-\bar{x}}{s}\] onde:
z = escore z
$\begin{aligned} \bar{x} = \text{média} \end{aligned}$
s = desvio padrão
x = valor a partir do qual iremos calcular o escore z.

Para o jogador 2, o escore z é: \[z = \frac{60-40}{10}=2\]

O escore z fornece um padrão para compararmos valores de diferentes conjuntos de dados. Ele informa quantos desvios padrões um dado valor está distante em relação à média. Um escore z positivo indica um valor acima da média, enquanto que um escore z negativo indica um valor abaixo da média.

O escore z é muito utilizado na análise estatística. A figura 3.14 mostra curvas de crescimento (peso por idade) para meninas do nascimento até 5 anos, padronizadas pela OMS, semelhantes às da figura 3.10, porém agora as curvas são construídas por meio dos escores z. Então, para uma menina de certa idade, mede-se o seu peso e verificamos qual o seu escore z aproximado, observando entre quais escores z o seu peso se situa na curva de crescimento. Assim é possível verificar como está o desenvolvimento dessa criança em relação ao esperado na população.

Os escores padrão (escores z) não são propriamente medidas de dispersão, mas sim uma forma de indicar como um valor se situa em relação aos valores da variável de onde ele se origina. Nesse sentido, ele pode ser utilizado para detectar possíveis dados desviantes (outliers) no conjunto de dados. Por exemplo, às vezes outliers são considerados aqueles dados que se afastam mais de 3 desvios padrões da média (escore z < -3 ou escore z > 3).

O escore z também pode ser usado para comparar diferentes valores em variáveis diferentes, mesmo quando essas variáveis possuem diferentes médias e desvios padrões.

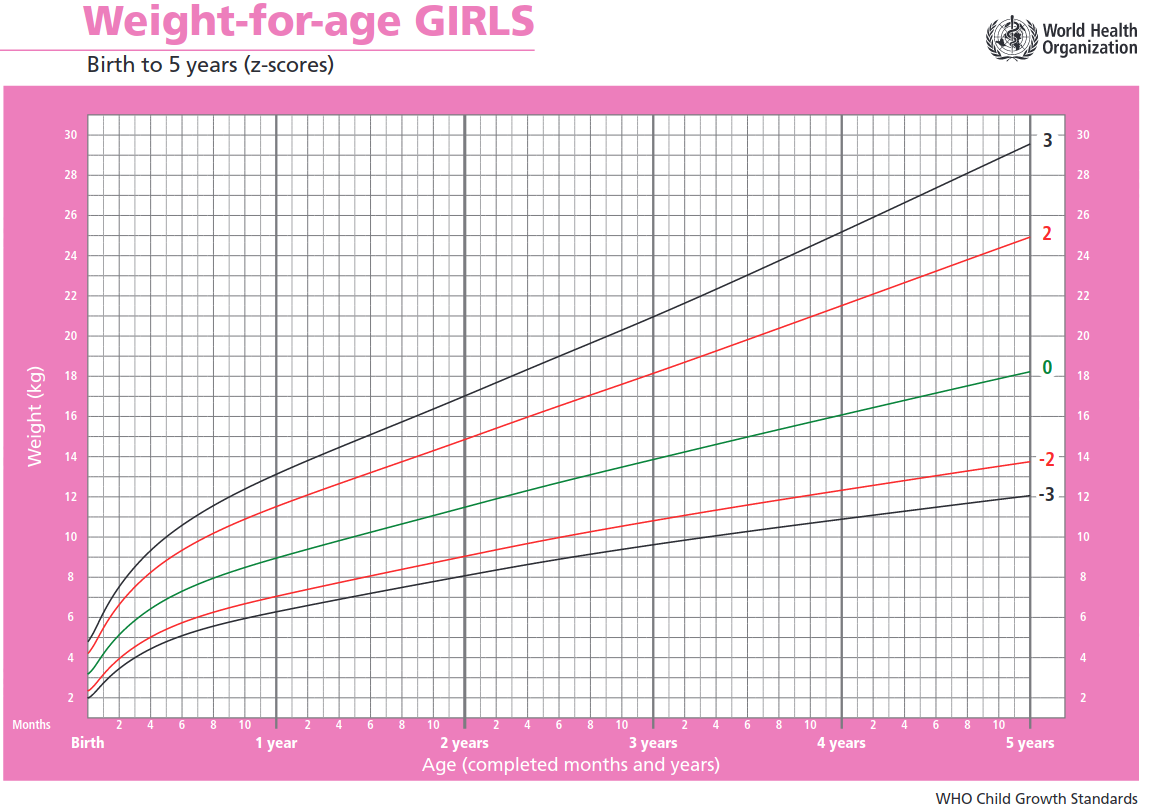
Curvas de crescimento padronizadas pela OMS, semelhante à da figura 3.10, porém as curvas são construídas a partir dos escores z. Fonte: Organização Mundial de Saúde (CC BY-NC-SA 3.0 IGO).

Figura 3.14: Curvas de crescimento padronizadas pela OMS, semelhante à da figura 3.10, porém as curvas são construídas a partir dos escores z. Fonte: Organização Mundial de Saúde (CC BY-NC-SA 3.0 IGO).

3.6 Obtendo estatísticas descritivas no R

Nesta seção, iremos utilizar o R Commander para obter as medidas de tendência central e dispersão de variáveis e também aprender mais alguns recursos dessa interface gráfica.

Os conteúdos das subseções desta seção podem ser visualizados neste vídeo.

3.6.1 Carregando conjuntos de dados de pacotes do R

Nesta seção, vamos carregar um outro conjunto de dados já disponível em um pacote do R. Trata-se do conjunto de dados juul2 do pacote ISwR (GPL-2 | GPL-3).

Nós já instalamos o pacote ISwR na seção 2.2.

Antes de abrirmos o conjunto de dados juul2, é preciso carregar o pacote ISwR. Na área de script do R Commander, digitamos library(ISwR) e, com o cursor na linha do comando, clicamos no botão Submeter (figura 3.15).

Figura 3.15: Tela do R commander, com a digitação da função library(ISwR) na área de Script.

A função library(ISwR) carregou a biblioteca ISwR. Para abrir o conjunto de dados juul2, vamos seguir um procedimento análogo ao utilizado para abrir o conjunto de dados stroke na seção 2.2, que será mostrado novamente a seguir.

Vamos selecionar a opção a seguir no R Commander:

\[\text{Dados} \Rightarrow \text{Conjunto de dados em pacotes} \Rightarrow \text{Ler dados de pacotes 'atachados'}\]

Na tela Leia dados do pacote, para ver a lista dos conjuntos de dados em ISwR, damos um duplo clique nesse pacote e uma lista de conjuntos de dados será mostrada à direita (figura 3.16). Rolamos essa lista e clicamos no conjunto de dados juul2 para selecioná-lo (figura 3.16).

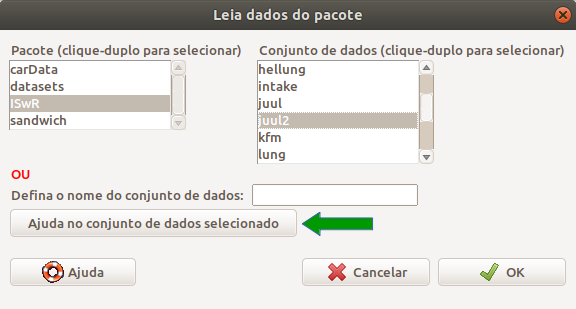
Figura 3.16: Visualizando a lista de conjuntos de dados do pacote ISwR e selecionando o conjunto juul2.

Para conhecermos a estrutura desse conjunto de dados, clicamos no botão Ajuda para o conjunto de dados selecionado (seta verde na figura 3.16). Uma descrição desse conjunto de dados será exibida na janela de seu navegador padrão (figura 3.17). Ao clicarmos no botão OK na figura 3.16, após termos selecionado juul2, esse conjunto de dados será carregado no R Commander (figura 3.18).

Figura 3.17: Texto com a descrição do conjunto de dados juul2 exibido no navegador padrão.

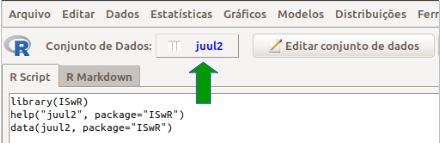
Figura 3.18: Tela do R Commander após o carregamento do conjunto de dados juul2. Observem a função que foi executada – data(juul2, package="ISwR") – e o nome do conjunto selecionado (seta verde).

Na área de mensagens do R Commander, aparece a seguinte mensagem abaixo do comando, indicando o número de registros e de variáveis no conjunto de dados juul2:

NOTA: Os dados juul2 tem 1339 linhas e 8 colunas.

3.6.2 Obtendo resumos numéricos pelo R Commander

O conjunto de dados juul2 possui 1339 registros, cada registro com valores de 8 variáveis. Ele contém uma amostra da distribuição da variável insulin-like growth factor (igf1), com os dados coletados em exames físicos, sendo a maior parte dos dados de pessoas em idade escolar, mas também inclui outras faixas etárias. Vamos obter algumas medidas de tendência central e dispersão para as variáveis idade e igf1.

No item de menu Estatística, clique em Resumos e, a seguir, em Resumos numéricos:

\[\text{Estatísticas} \Rightarrow \text{Resumo...} \Rightarrow \text{Resumos numéricos...}\]

Na tela Resumos Numéricos, selecionamos as variáveis na aba Dados. Para selecionarmos mais de uma variável, mantemos a tecla Ctrl pressionada enquanto clicamos nas variáveis desejadas. Nesse exemplo, vamos selecionar as variáveis age e igf1 (Figura 3.19). Em seguida, clicamos na aba Estatísticas (seta verde).

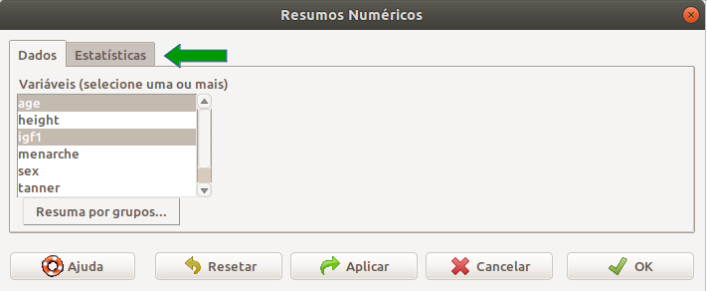
Seleção das variáveis para as quais um resumo numérico será mostrado. A seta verde indica a aba onde podem ser selecionadas as medidas que serão apresentadas.

Figura 3.19: Seleção das variáveis para as quais um resumo numérico será mostrado. A seta verde indica a aba onde podem ser selecionadas as medidas que serão apresentadas.

Na aba Estatísticas (figura 3.20), observem que as medidas média, desvio padrão, distância interquartil e quantis já estão marcadas. Se desejarmos outros quantis, basta digitá-los na caixa de texto com o rótulo Quantis, separados por vírgula, não esquecendo que o separador de decimal no R é o ponto. Ao clicarmos em OK, os resultados serão apresentados ou na console do RStudio (figura 3.21) ou na área de resultados (Output) do R Commander, caso o R Commander tenha sido carregado a partir do RStudio ou não, respectivamente.

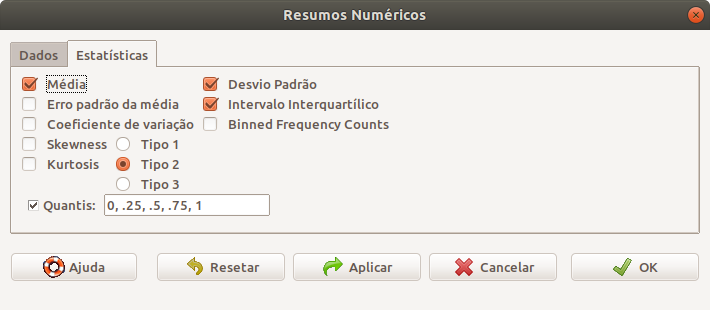
Figura 3.20: Tela para a seleção das medidas que serão apresentadas no resumo numérico.

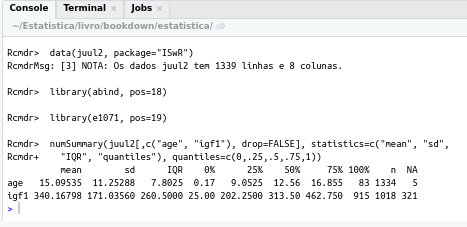
Figura 3.21: Resumos numéricos para as variáveis age e igf1.

Observem que as medidas são calculadas corretamente, mesmo considerando que, em alguns registros, alguns dados não foram preenchidos. Dados ausentes são indicados por NA (not available, em inglês). Os resultados indicam que 5 registros não possuem valores para idade e 321 registros não possuem valores de igf1.

Se formos usar as funções para obter essas medidas individualmente, poderemos ter problemas. Por exemplo, digitando a função mean(juul2$age) na área de script do R Commander e clicando no botão Submeter, o resultado será NA (figura 3.22). Isso ocorreu devido aos 5 registros sem valores de idade. O comando mean(juul2$age) também poderia ser executado na console do RStudio.

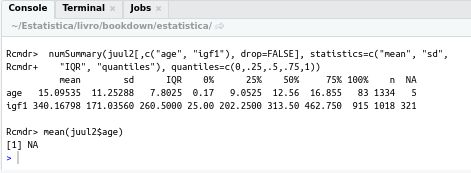
Figura 3.22: Resultado da função mean(juul2$age) na presença de valores ausentes.

Na função mean(juul2$age), a variável age é precedida do nome do conjunto de dados e do símbolo $. Essa é a sintaxe utilizada para referenciar uma variável que faz parte de um conjunto de dados:

conjuntoDeDados$nomeDaVariável

Para calcular a média, não incluindo os registros com valores ausentes, usamos o argumento na.rm=TRUE, o qual sinaliza para remover do cálculo os registros com valores ausentes. Assim, para obtermos a média de idade, usamos a função abaixo:

mean(juul2$age, na.rm=TRUE)

Agora a média será obtida corretamente (figura 3.23).

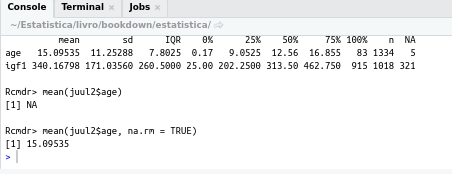
Figura 3.23: Obtendo a média de idade corretamente por meio da função mean(juul2$age, na.rm=TRUE).

3.6.3 R Markdown

O R Markdown é uma linguagem que permite que um relatório possa ser gerado a partir dos comandos que vão sendo executados no R. No R Commander, ele pode ser visualizado na aba R Markdown (seta verde na figura 3.24).

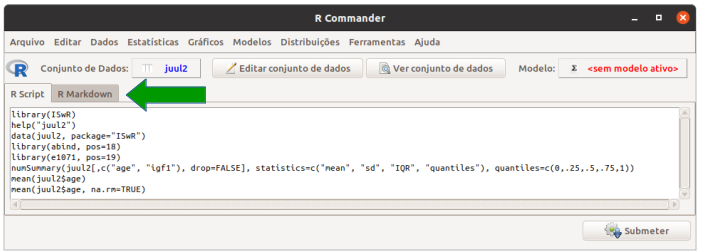
Figura 3.24: Acessando a aba R Markdown no R Commander.

Esse relatório pode ser personalizado pelo usuário. Por exemplo, no texto da figura 3.25, alteramos o título e o autor (seta verde na figura), depois selecionamos o comando help… (figura 3.26) e o apagamos (figura 3.27) para não exibir a ajuda do conjunto de dados em uma outra página web quando for gerado o relatório. Ao clicarmos no botão Gerar relatório, o relatório será apresentado no navegador padrão de seu computador (figura 3.28).

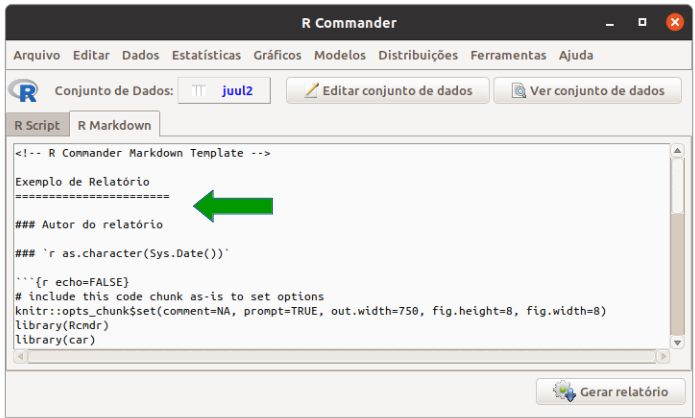
Figura 3.25: Personalizando o título e o autor do relatório no R Markdown.

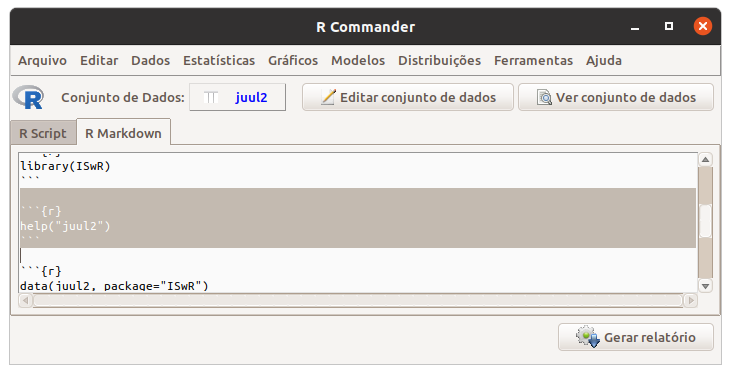
Figura 3.26: Selecionando partes do relatório para edição.

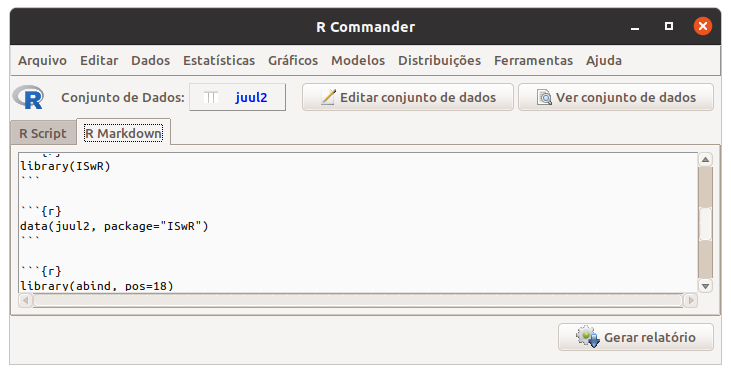
Figura 3.27: Remoção da área selecionada na figura 3.26.

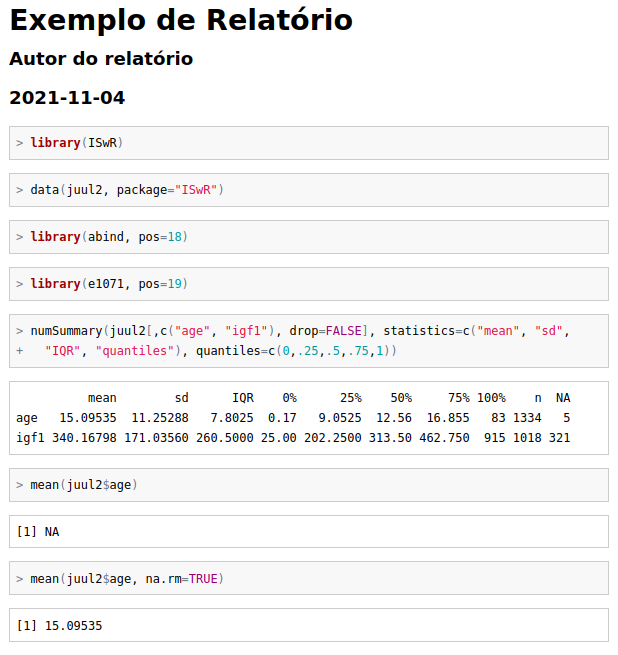
Figura 3.28: Relatório gerado pelo R Markdown em html para os comandos utilizados nesta seção.

3.6.4 Salvando scripts e arquivos do R Markdown

Todos os comandos utilizados numa seção do R Commander podem ser salvos em um arquivo. É possível também editar os comandos, inclusive removê-los, na janela de Script antes de salvá-lo. Em outra seção do R Commander ou R Studio, o arquivo salvo pode ser reaberto e os comandos executados, sem necessidade de executar cada um deles individualmente.

Para salvar o script no R Commander, selecionamos a seguinte opção:

\[\text{Arquivo} \Rightarrow \text{Salvar script como...}\]

Na janela Salvar como (figura 3.29), selecionamos a pasta onde o arquivo será gravado e digitamos o nome do mesmo na caixa de texto Nome do Arquivo. Vamos manter a extensão do arquivo (.R). Em seguida, clicamos no botão Salvar e o arquivo será gravado na pasta desejada.

Figura 3.29: Selecionando a pasta e digitando o nome do script a ser gravado.

Para salvar o arquivo gerado na aba R Markdown, selecionamos a seguinte opção.

\[\text{Arquivo} \Rightarrow \text{Salvar arquivo R Markdown como...}\]

Na janela Salvar como (figura 3.30), selecionamos a pasta onde o arquivo será gravado e digitamos o nome do mesmo na caixa de texto Nome do Arquivo. Vamos manter a extensão do arquivo (.Rmd). Em seguida, clicamos no botão Salvar e o arquivo será gravado na pasta desejada.

Figura 3.30: Selecionando a pasta e digitando o nome do arquivo do R Markdown a ser gravado.

3.7 Executando scripts no R Commander

Se, na aba R Script, selecionarmos um conjunto de comandos ao mesmo tempo e clicarmos no botão Submeter, os comandos serão executados em sequência de maneira automática (figura 3.31) e os resultados serão exibidos ou na console do R Studio ou na área de resultados (Output) do R Commander, caso o R Commander tenha sido carregado a partir do RStudio ou não, respectivamente.

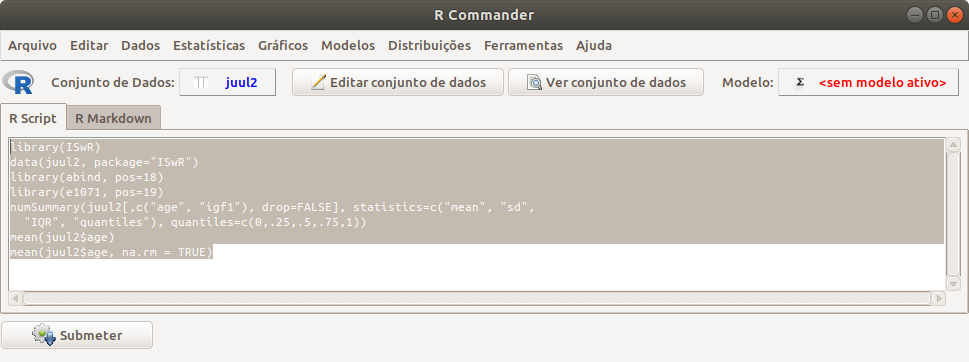
Figura 3.31: Execução automática e em sequência de um conjunto de comandos selecionados na aba R Script.

3.8 Exercícios

No estudo intitulado “Capacidade preditiva de indicadores antropométricos para o rastreamento da dislipidemia em crianças e adolescentes” (Quadros et al. 2015), os resultados de colesterol total, HDL, LDL e triglicerídios são apresentados na figura 3.32 por sexo e faixa etária.
1. A apresentação dos valores de média e desvio padrão são adequados? Justifique.
2. Qual a sua opinião sobre o por que de os autores apresentarem os resultados de triglicerídios como mediana e percentis 25 e 75 e não como média e desvio padrão?
3. Qual a distância interquartil de triglicerídeos para o sexo feminino?

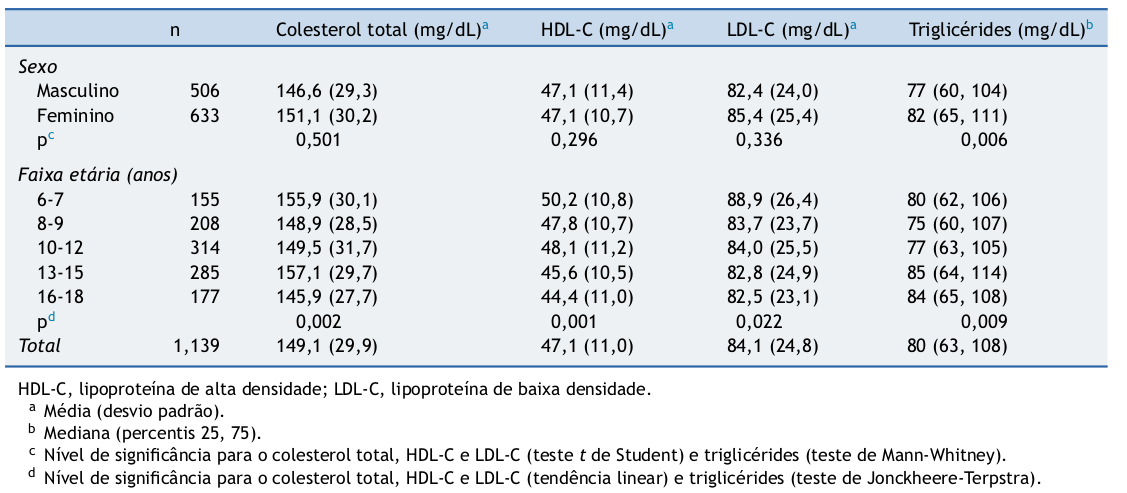
Figura 3.32: Tabela 2 do estudo de (Quadros et al. 2015) (CC-BY-NC-ND).

A tabela a seguir (figura 3.33) foi extraída de um estudo que avalia a associação entre o distúrbio ventilatório restritivo (DVR) e o risco cardiovascular e nível de atividade física em adultos assintomáticos.
1. Como são apresentadas as medidas de tendência central e dispersão para as variáveis numéricas?
2. Essa forma de apresentação é adequada? Justifique a sua resposta.
3. Se a resposta à questão (c) é negativa, que modo de apresentação você sugeriria?
4. Para a variável CVF, é correto afirmar que 68,3% dos valores estão situados entre 2,92 e 4,92 litros no grupo dos pacientes com padrão espirométrico normal? Justifique a sua resposta.

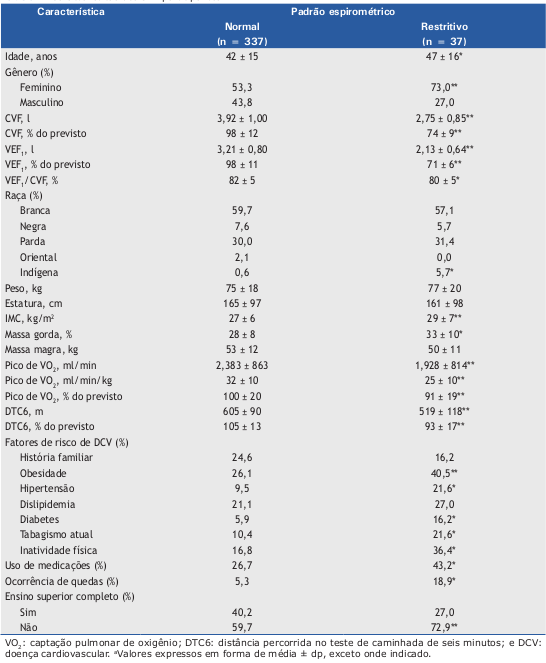
Figura 3.33: Tabela 1 do estudo de (Sperandio et al. 2016) (CC-BY-NC).

Com o conjunto de dados VA do pacote MASS (GPL-2 | GPL-3) do R, faça as atividades abaixo.
1. Verifique a ajuda para o conjunto de dados.
2. Carregue o conjunto de dados.
3. Visualize os registros do conjunto de dados.
4. Verifique as seguintes estatísticas para as variáveis diag.time e stime: mínimo, máximo, média, mediana, P₂₅, P₇₅ e número de observações.

Com o conjunto de dados Melanoma do pacote MASS do R, faça as atividades abaixo.
1. Verifique a ajuda para o conjunto de dados.
2. Carregue o conjunto de dados.
3. Visualize os registros do conjunto de dados.
4. Verifique as seguintes estatísticas para as variáveis time e thickness: mínimo, máximo, média, mediana, P₂₅, P₇₅ e número de observações.

Referências

Griffiths, Dawn. 2008. Head First Statistics. Cambridge: O’Reilly.

Harding, David. 1996. “The Range of a Set of Data.” Teaching Statistics 18 (1): 81.

Quadros, Teresa Maria Bianchini, Alex Pinheiro Gordia, Rosane Carla Rosendo Silva, and Luciana Rodrigues Silva. 2015. “Capacidade Preditiva de Indicadores Antropométricos Para o Rastreamento Da Dislipidemia Em Crianças e Adolescentes.” Jornal de Pediatria 91 (5): 455–63. https://doi.org/http://dx.doi.org/10.1016/j.jped.2014.11.006.

Sperandio, Evandro Fornias, Rodolfo Leite Arantes, Agatha Caveda Matheus, Rodrigo Pereira Silva, Vinícius Tonon Lauria, Marcello Romiti, Antônio Ricardo de Toledo Gagliardi, and Victor Zuniga Dourado. 2016. “Distúrbio Ventilatório Restritivo Sugerido Por Espirometria: Associação Com Risco Cardiovascular e Nível de Atividade Física Em Adultos Assintomáticos.” J Bras Pneumol 42 (1): 22–28. https://doi.org/http://dx.doi.org/10.1590/S1806-37562016000000030.