11 Funções densidade de probabilidades

11.1 Introdução

Até agora vimos os conceitos fundamentais da teoria de probabilidades e distribuição de probabilidades, assumindo que temos conhecimento da probabilidade de eventos ou que a variável aleatória é discreta. Vimos no capítulo 1 que, devido às limitações da precisão dos instrumentos de medida, a rigor, todas as variáveis numéricas poderiam ser consideradas discretas na prática. Entretanto é bastante útil realizar uma simplificação aqui e considerar uma situação teórica em que os instrumentos de medida possuem precisão ilimitada. Nesse caso, vamos considerar que variáveis numéricas como tempo, peso, altura, etc, podem assumir qualquer valor real dentro de um dado intervalo. Vamos agora verificar que, para obter probabilidades e distribuições de probabilidades para variáveis aleatórias contínuas, será preciso introduzir os conceitos de densidade de probabilidade e integral de uma função.

11.2 Histograma de variáveis contínuas. Recordação

Os conteúdos desta seção e das seções 11.3, 11.4 e 11.5 podem ser visualizados neste vídeo.

Vamos retornar a dois histogramas criados no capítulo 4 para visualizar a distribuição dos valores da variável igf1 (fator de crescimento semelhante à insulina tipo 1) do conjunto de dados juul2. Os histogramas são baseados na tabela 11.1, cópia da tabela 4.2.

O histograma de frequência relativa para a variável igf1 é mostrado na figura 11.1. Podemos considerar a frequência relativa de cada classe como a probabilidade de obtermos um valor dentro desta classe se escolhermos aleatoriamente um valor de igf1 dentre os valores possíveis de igf1 no conjunto de dados.

Tabela 11.1: Definição das classes de um histograma e respectivas frequências, frequências relativas e densidade de frequência relativa para a variável igf1 do conjunto de dados juul2.

Classe	Limite Inferior (\(\gt\))	Limite Superior (\(\leq\))	Frequência	Frequência Relativa (%)	Densidade de Frequência Relativa (x 10-3)
1	0	100	43	4,22	0,42
2	100	150	74	7,27	1,45
3	150	200	130	12,77	2,55
4	200	250	129	12,67	2,53
5	250	300	118	11,59	2,32
6	300	350	69	6,78	1,36
7	350	400	94	9,23	1,85
8	400	450	93	9,14	1,82
9	450	500	92	9,04	1,80
10	500	600	98	9,63	0,96
11	600	1000	78	7,66	0,19
			1018	100

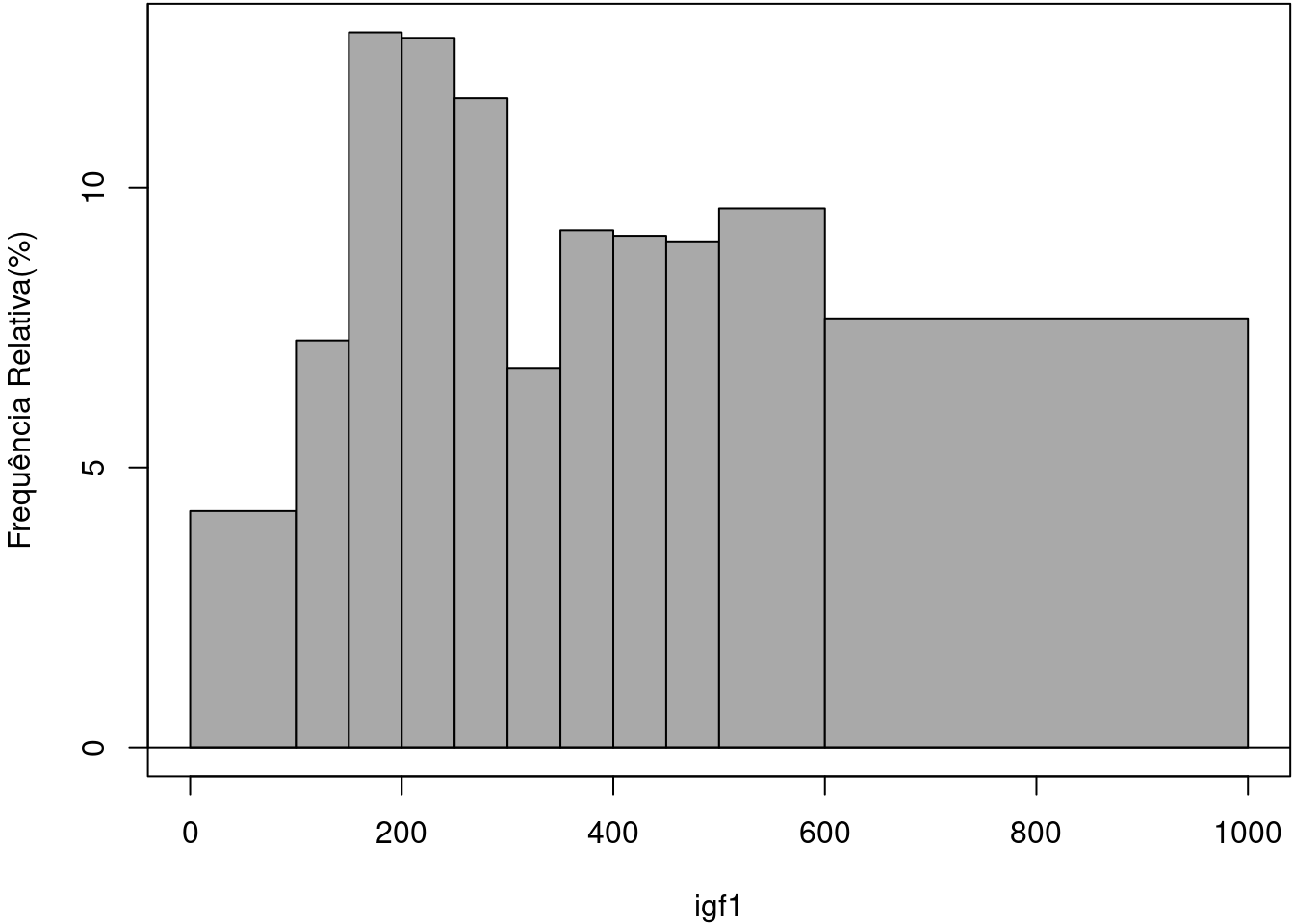
Figura 11.1: Histograma de frequência relativa da variável igf1 para as classes definidas conforme a tabela 11.1.

Relembrando a discussão apresentada no capítulo 4, observem que a classe 10, que vai de 500 a 600 possui 98 elementos (9,6% do total de valores de igf1) e a classe 11, que vai de 600 a 1000 possui 78 elementos (7,7% do total de valores de igf1). Apesar de o histograma mostrar que a altura da classe 10 é pouco maior do que a da classe 11, é importante ter em mente que os 98 elementos da classe 10 estão distribuídos em um intervalo de amplitude 100, enquanto que os 78 elementos da classe 11 estão distribuídos em um intervalo de amplitude 400 (1000 - 600), ou seja, a densidade da classe 10 é bem maior do que a da classe 11 e este fato não é mostrado pelo histograma de frequência relativa. Isso pode ser contornado, construindo-se o histograma de tal modo que a área de cada classe (amplitude da classe x altura) seja igual à sua frequência relativa. Para isso, dividimos a frequência relativa de cada classe por sua amplitude, obtendo então a densidade de frequência relativa da classe (coluna 6 da tabela 11.1). O histograma assim construído é denominado histograma de densidade de frequência relativa (figura 11.2).

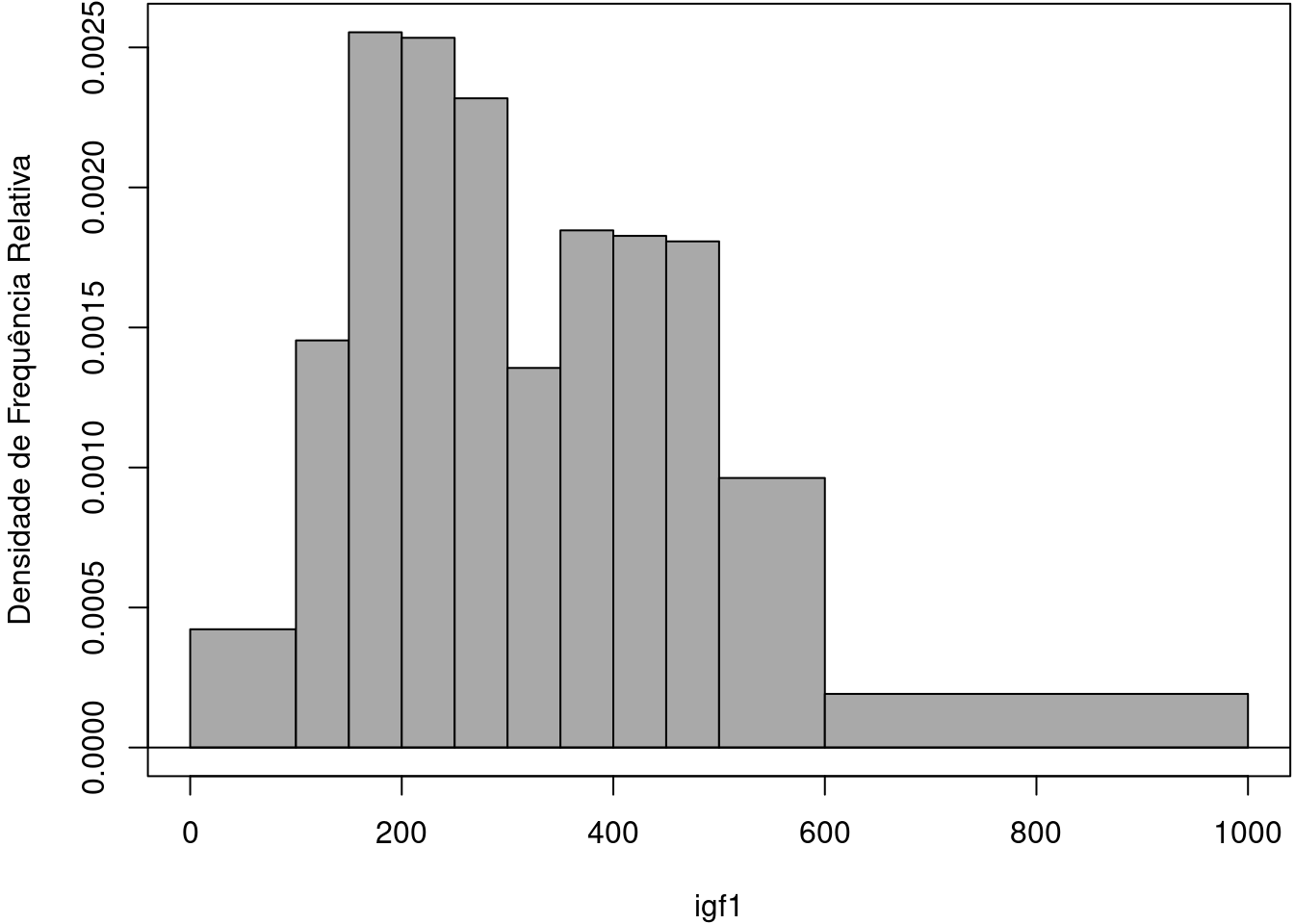
Figura 11.2: Histograma de densidade de frequência relativa da variável igf1 para as classes definidas conforme a tabela 11.1.

Observem agora que a altura da classe 11 é relativamente bem menor do que a das demais classes, refletindo o fato de que os 78 valores dessa classe estão distribuídos em uma faixa maior de valores do que as demais classes, mas a área dessa classe é igual à sua frequência relativa. Também observem que a área de cada classe sob o histograma de densidade de frequência fornece a frequência relativa daquela classe, ou a probabilidade de obtermos um valor dentro dessa classe se escolhermos aleatoriamente um valor de igf1 dentre os valores possíveis de igf1 no conjunto de dados.

Vamos aplicar esse raciocínio para chegarmos às funções densidade de probabilidade e funções de distribuição de probabilidades para variáveis contínuas.

11.3 Função densidade de probabilidade

Vamos inicialmente realizar um experimento que você pode reproduzir, acessando a aplicação Densidade de Frequência e Distribuição Acumulada. A tela inicial dessa aplicação é mostrada na figura 11.3. O experimento consiste em considerar uma variável aleatória que é o peso de uma pessoa escolhida aleatoriamente de uma população de pessoas com média 70 kg e desvio padrão de 10 kg. Inicialmente vamos escolher aleatoriamente 20.000.000 pessoas dessa população, de modo que teremos 20.000.000 valores da nossa variável aleatória. Histogramas de frequência relativa, densidade de frequência e distribuição cumulativa da densidade de frequência são então plotados para esses 20.000.000 valores, bem como uma tabela de frequência com as seis classes centrais dos histogramas é construída.

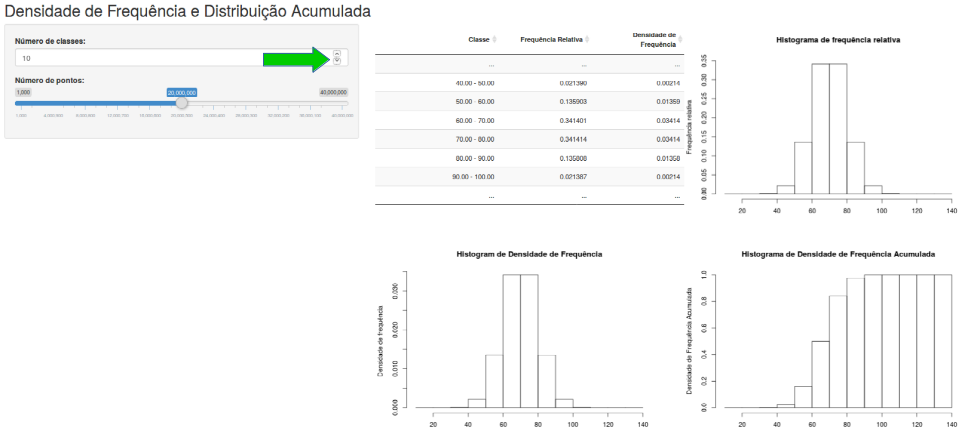
Figura 11.3: Tabelas de frequência, histogramas de frequência relativa, densidade de frequência e distribuição cumulativa de densidade de frequência para uma variável aleatória com média 70 e desvio padrão 10 para um certo número de classes no histograma (10 inicialmente) e um certo número de valores da variável aleatória escolhida aleatoriamente (inicialmente 20.000.000). O número de classes do histograma pode ser alterado ao clicarmos na seta para cima ou para baixo ou digitando o valor desejado na caixa de texto correspondente.

Vamos começar com 10 classes. Vamos variar esse número de classes de 10 para 100, e depois 1000, e ver o que acontece com o histograma da frequência relativa (figura 11.4). Para cada histograma, a amplitude (largura) de cada classe é a mesma.

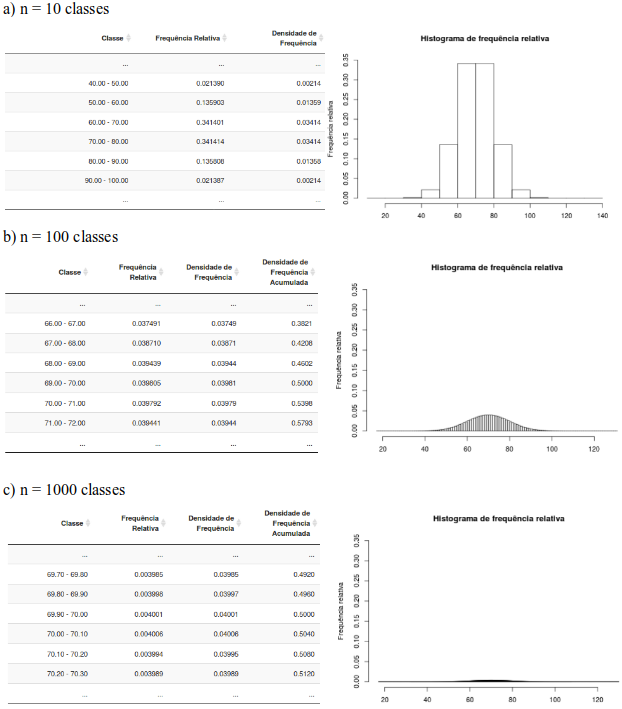
Figura 11.4: Tabela de frequência e histograma de frequência relativa da aplicação da figura 11.3, para diversos valores para o número de classes (a-10, b-100 e c-1000).

Observem que, à medida que o número de classes do histograma aumenta, o histograma se aproxima cada vez mais de uma linha contínua, a amplitude de cada classe diminui, assim como a frequência relativa de cada classe. O valor máximo da frequência relativa cai de ~ 0,34 para 10 classes para menos de 0,004 para 1000 classes.

Assim, se fizermos um exercício mental e aumentarmos o número de valores aleatórios extraídos da população indefinidamente e criarmos um histograma de frequência relativa aumentando indefinidamente o número de classes, veremos que a frequência relativa de cada classe irá aproximar-se cada vez mais de zero! Ora, ao aumentarmos indefinidamente o número de classes, a amplitude de cada intervalo irá convergir para zero e cada classe irá ser constituída de um único ponto. Como a frequência relativa de uma classe é uma estimativa da probabilidade de obtermos um valor dentro da classe, então a probabilidade de obtermos um valor específico dentre os valores possíveis da variável é zero!

Ao alterarmos o número de classes no histograma, a aplicação também mostra os respectivos histogramas de densidade de frequência e da distribuição cumulativa de densidade de frequência relativa (figura 11.5).

Observem que, analogamente aos histogramas de frequência relativa, os histogramas de densidade e distribuição cumulativa da densidade de frequência se aproximam de uma curva contínua à medida que o número de classes aumenta. Porém, ao contrário dos histogramas de frequência relativa, as alturas das classes no histograma de densidade de frequência não se aproximam de zero , mantendo-se relativamente constantes, à medida que o número de classes aumenta. Lembramos que a densidade de frequência de cada classe é obtida dividindo-se a frequência relativa da classe por sua amplitude. Assim, apesar de a frequência relativa de cada classe diminuir à medida que o número de classes aumenta, a amplitude da classe também diminui proporcionalmente, de modo que a densidade de frequência (divisão da frequência relativa pela amplitude da classe) tende a um valor constante.

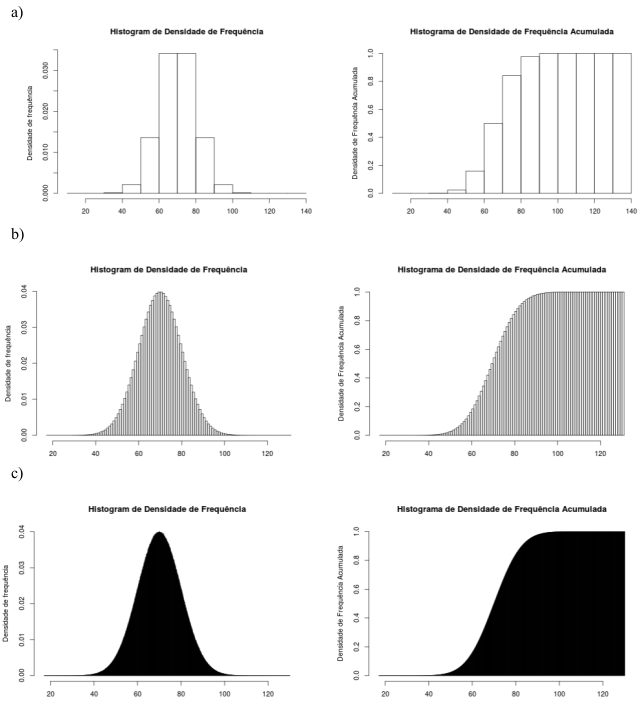
Figura 11.5: Histograma da densidade de frequência relativa e da distribuição cumulativa da densidade de frequência relativa da aplicação da figura 11.3, para diversos valores para o número de classes (a-10, b-100, c-1000).

Da mesma forma que interpretamos a frequência relativa como estimativas de probabilidades, podemos interpretar as densidades de frequências relativas como estimativas das densidades de probabilidades. Portanto não há sentido em termos uma distribuição de probabilidades para variáveis contínuas, já que a probabilidade de ocorrência de cada valor da variável é zero. Mas podemos falar numa função densidade de probabilidade.

Analogamente ao caso de uma variável discreta, a \(P(X \le x_0)\) para uma variável contínua é igual à probabilidade cumulativa para X = x₀, correspondendo à probabilidade de se obter um valor menor ou igual a x₀. À função \(F(x) = P(X \le x_0)\) para todos os valores de x, chamamos de função de distribuição (ou de probabilidade cumulativa). Vamos aprofundar um pouco mais a relação entre a função densidade de probabilidade e a função de distribuição, introduzindo o conceito de integral de uma função.

11.4 Integral da função densidade de probabilidade

Como obter a função de distribuição a partir da função densidade de probabilidade? Sabemos que o histograma da distribuição cumulativa da densidade de frequência relativa é obtido a partir do histograma da densidade de frequência relativa, somando-se, para cada ponto de uma dada classe, a área dessa classe e as áreas das classes que a precedem. Vamos rodar a aplicação Integracao (figura 11.6).

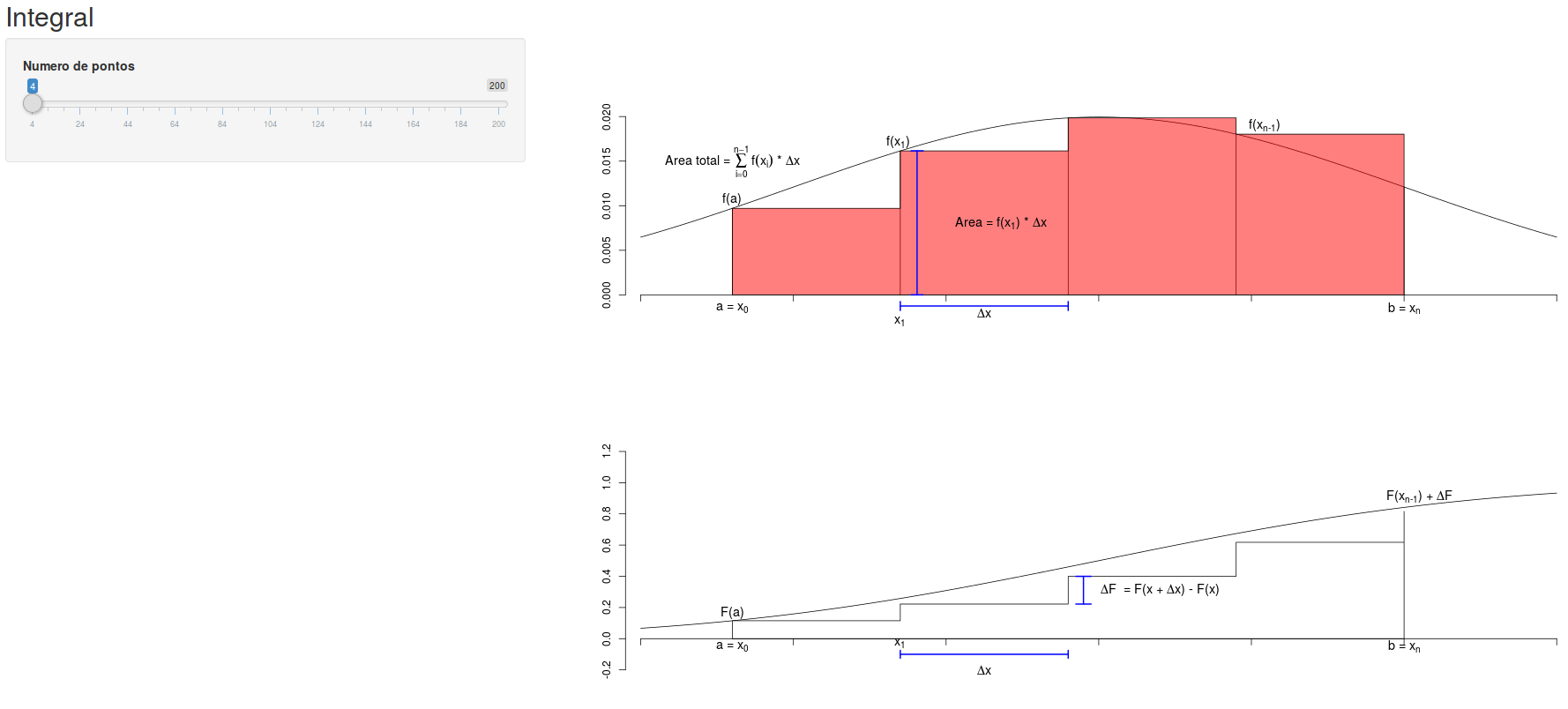
Figura 11.6: Obtenção aproximada da função de distribuição a partir da função densidade de probabilidade, construindo-se histogramas sucessivos com um número crescente de classes. A aplicação é iniciada com um histograma com quatro classes.

Nessa aplicação, vamos considerar que temos uma função densidade de probabilidade f(x) cuja curva está mostrada no gráfico superior e desejamos saber a probabilidade de obtermos um valor da variável aleatória X entre \(a\) e \(b\) (\(P(a \le X \le b)\)). A partir da função de distribuição (gráfico inferior), essa probabilidade seria dada por \(F(X=b) - F(X=a)\). Porém vamos supor que não conhecemos a função de distribuição e temos somente a função densidade de probabilidade. Poderíamos aproximar a área da função densidade de probabilidade entre \(a\) e \(b\) por quatro retângulos, cada um com base igual a \(\Delta x = (b - a) / 4\). Então o valor da função de distribuição em b seria igual à soma das áreas dos quatro retângulos mais o valor da função de distribuição em \(a\). O primeiro retângulo teria área igual a \(f(a).\Delta x\), o segundo retângulo área igual a \(f(x_1).\Delta x\), e assim por diante, de modo que a soma das áreas dos quatro retângulos poderia ser expressa por:

\(\begin{aligned} \ \text{Área} \sim F(X=b) - F(X=a) =\sum_{i=0}^{3}f(x_i)\Delta x \end{aligned}\)

Podemos observar que essa aproximação é um tanto imprecisa. Podemos melhorá-la, aumentando o número de classes (retângulos). Ao aumentarmos o número de classes para 8, obtemos a figura 11.7.

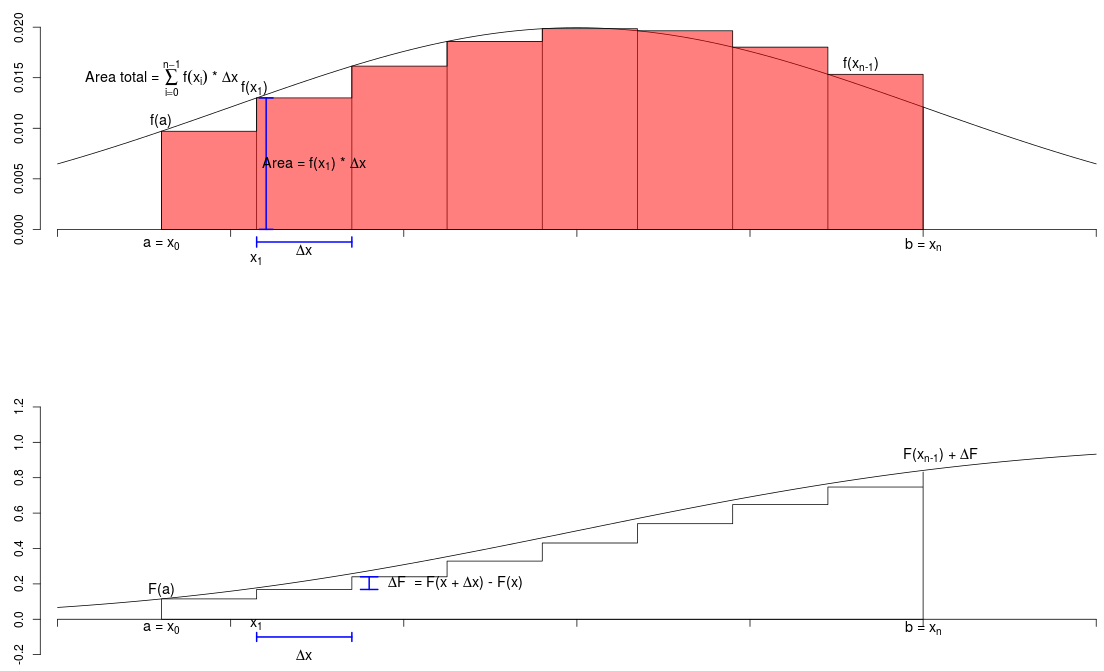
Figura 11.7: Obtenção aproximada da função de distribuição a partir da função densidade de probabilidade, utilizando um histograma com oito classes.

A aproximação é um pouco melhor, e a área dos 8 retângulos seria dada por:

\(\begin{aligned} \ \text{Área} \sim F(X=b) - F(X=a) =\sum_{i=0}^{7}f(x_i)\Delta x \end{aligned}\)

À medida que o número de classes aumenta, a aproximação fica cada vez melhor. Com 200 classes, obtemos a figura 11.8. A aproximação nesse caso já é bastante boa. O limite da soma das áreas dos retângulos obtida quando aumentamos indefinidamente o número de retângulos, sendo a amplitude de cada um deles cada vez menor, é a área sob a curva densidade de probabilidade compreendida entre os pontos \(a\) e \(b\). Esse limite é a integral da função densidade de probabilidade entre os pontos \(a\) e \(b\) e podemos escrever matematicamente:

\[\begin{align} \text{Área sob f(x) entre}\ a\ \text{e}\ b = F(X=b) - F(X=a) &=\int_{a}^{b}f(x)dx= \lim_{n\to\infty, \Delta x\to 0}\sum_{0}^{n}f(x_i)\Delta x \tag{11.1} \end{align}\]

onde o símbolo \(\int\) é o sinal de integração. O conceito de integração é um conceito fundamental do cálculo e possui inúmeras aplicações, além do cálculo de probabilidades. Por exemplo, dada a função de velocidade de um corpo, a área sob o gráfico da velocidade, ou seja, a integral da velocidade, fornece a distância percorrida. Em um outro exemplo, dada a densidade linear de uma barra, a integral da densidade linear fornece a massa da barra.

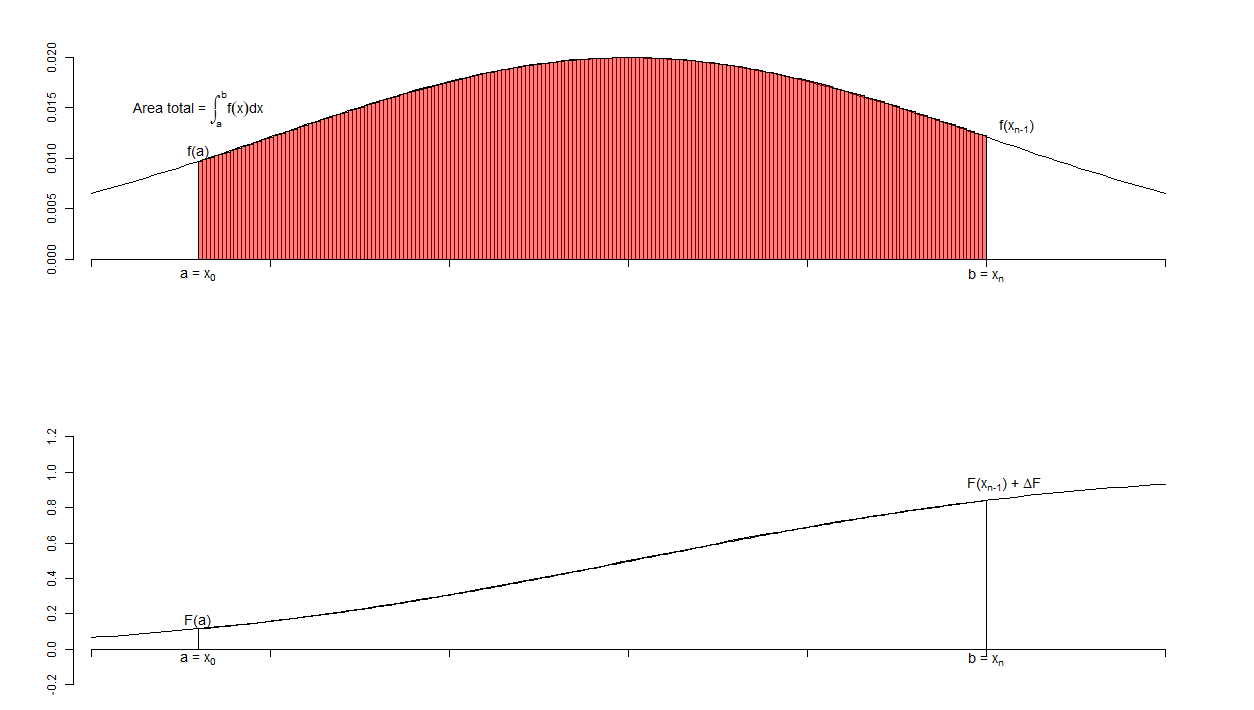
Figura 11.8: Obtenção aproximada da função de distribuição a partir da função densidade de probabilidade, utilizando um histograma com 200 classes.

11.5 Propriedades da função densidade de probabilidade

As propriedades descritas no capítulo 7 sobre probabilidades, bem como o teorema de Bayes se aplicam diretamente para funções densidade de probabilidades, lembrando apenas que agora estamos trabalhando com funções de densidade e não mais com valores de probabilidades específicas. Em particular, sendo f(x) uma função densidade de probabilidade, teremos:

(P1): f(x) é uma função sempre positiva;

(P2): Para o evento impossível, f(x) = 0;

(P3): Para o espaço amostral S que corresponde ao evento certo, \(\int_{-\infty}^{\infty}f(x)dx=1\), ou seja, a área total sob o gráfico da função densidade de probabilidade é sempre igual a 1;

(P4): Se um evento X for dividido em eventos disjuntos, ou mutuamente exclusivos, X₁, X₂, …, X_n (ou seja, se X_i, i = 1, 2, …, n, ocorre, os demais não ocorrerão), então a probabilidade do evento X será a soma das probabilidades de cada um dos eventos X_i. Matematicamente, isso será expresso por \(f(x)=\sum_{1}^{n}f(X_i)\). Levem em conta que cada evento X_i aqui pode se referir a um intervalo do conjunto dos números reais;

(P5): Se X e Y são dois eventos, então f(x,y) = f(x)f(y|x), onde f(y|x) é a função densidade de probabilidade condicional

Para o teorema de Bayes, como f(x,y) = f(x).f(y|x) = f(y).f(x|y), obtemos:

\[\begin{align} f(x|y) = \frac{f(x).f(y|x)}{f(y)} \tag{11.2} \end{align}\]

Para funções densidade de probabilidades, estamos trabalhando com funções contínuas, necessitando em muitos casos de resolver integrais para calcular probabilidades.

O valor esperado de uma variável aleatória X cuja função densidade de probabilidade é dada por f(x) é definido pela expressão:

\[\begin{align} E(X) &=\int_{-\infty}^{\infty} xf(x)dx \tag{11.3} \end{align}\]

e a variância é definida por :

\[\begin{align} var(X) &=\int_{-\infty}^{\infty} (x-E[X])^2f(x)dx = E[X^2]-(E[X])^2 \tag{11.4} \end{align}\]

A seguir, serão apresentadas algumas das principais funções densidade de probabilidade, a saber: distribuição uniforme, distribuição exponencial e distribuição normal.

11.6 Distribuição uniforme

Uma variável aleatória contínua X possui uma distribuição uniforme quando a sua função densidade de probabilidade possui um valor constante em um intervalo \([a, b]\) e zero fora desse intervalo. Logo, se f(x) é a função densidade da variável aleatória X, então:

\[\begin{align} \begin{split} f(X) = \begin{cases} \frac{1}{b-a},\ se\ a \le X \le b\\ 0,\ \text{caso contrário} \end{cases} \end{split} \tag{11.5} \end{align}\]

O valor constante é igual ao inverso da amplitude do intervalo \([a, b]\), porque a área sob o retângulo como base igual a \((b - a)\) tem que ser igual a 1. Lembremos que a área sob o gráfico da função densidade de probabilidade é igual a 1.

Por meio do R Commander, podemos visualizar o gráfico de um conjunto de funções de distribuição contínuas, de modo análogo ao caso de distribuições discretas. A figura 11.9 mostra como acessar a caixa de diálogo para obter o gráfico da distribuição uniforme.

Figura 11.9: Interface do R Commander com os menus de acesso para configurar o gráfico de uma distribuição uniforme.

A caixa de diálogo para estabelecer os parâmetros da distribuição uniforme é mostrada na figura 11.10. Os valores mínimo e máximo correspondem aos limites do intervalo \([a, b]\). Nesse exemplo, os valores para \(a\) e \(b\) são respectivamente 0 e 1. O gráfico da função de densidade de probabilidade é mostrado na figura 11.11a e o da função de distribuição de probabilidade cumulativa na figura 11.11b.

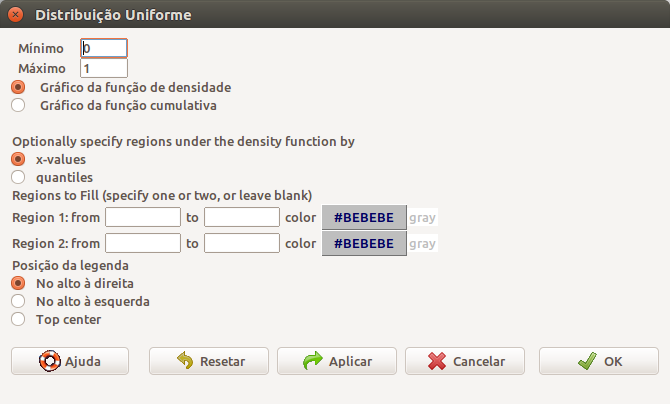
Figura 11.10: Caixa de diálogo do R Commander para configurar os parâmetros e gerar o gráfico de uma distribuição uniforme.

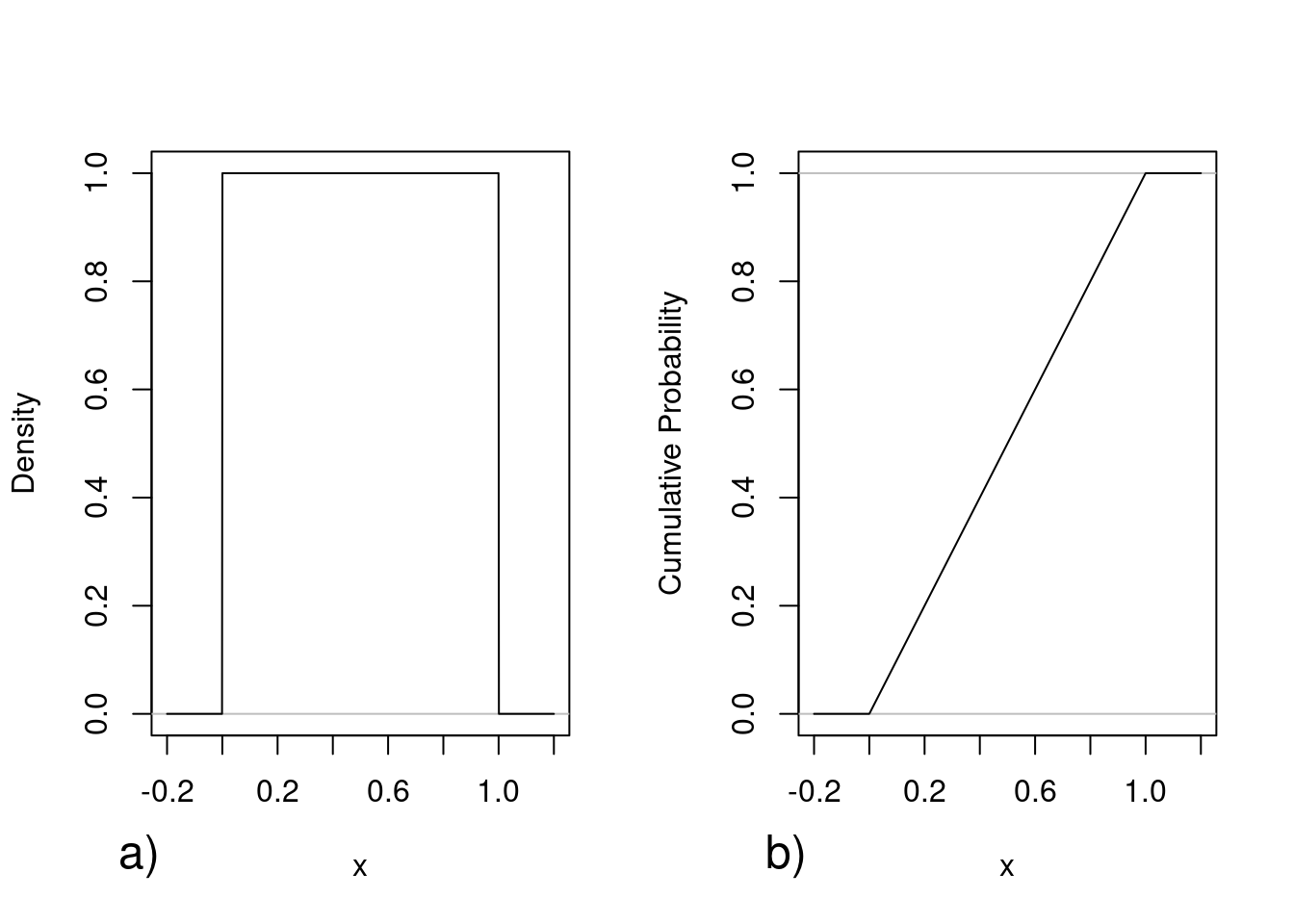
Figura 11.11: Gráfico da função de densidade de probabilidade (a) e o da função de distribuição de probabilidade cumulativa (b) para a distribuição uniforme com mínimo = 0 e máximo = 1.

Exemplo 1: dada uma distribuição uniforme com valores mínimo igual a 50 e máximo igual a 70, calcule a probabilidade de se obter um valor entre 50 e 55.

A função densidade de probabilidade dessa distribuição uniforme é dada por:

\(\begin{aligned} f(X) = \begin{cases} \frac{1}{20},\ se\ 50 \le X \le 70\\ 0,\ \text{caso contrário} \end{cases} \end{aligned}\)

Então a probabilidade de se obter um valor entre 50 e 55 é igual à área sob o gráfico da distribuição uniforme para os valores de X situados entre 50 e 55. Essa área é representada pela área hachurada da figura 11.12. Essa figura é obtida a partir da caixa de diálogo para obter o gráfico da distribuição uniforme (figura 11.10), estabelecendo os valores mínimo e máximo iguais a 50 e 70, respectivamente, e especificando os valores da Region1 from 50 to 55.

Logo:

\(\begin{aligned} \ P(50 \le X \le 55) = \frac{1}{20}(55-50)=0,25 \end{aligned}\)

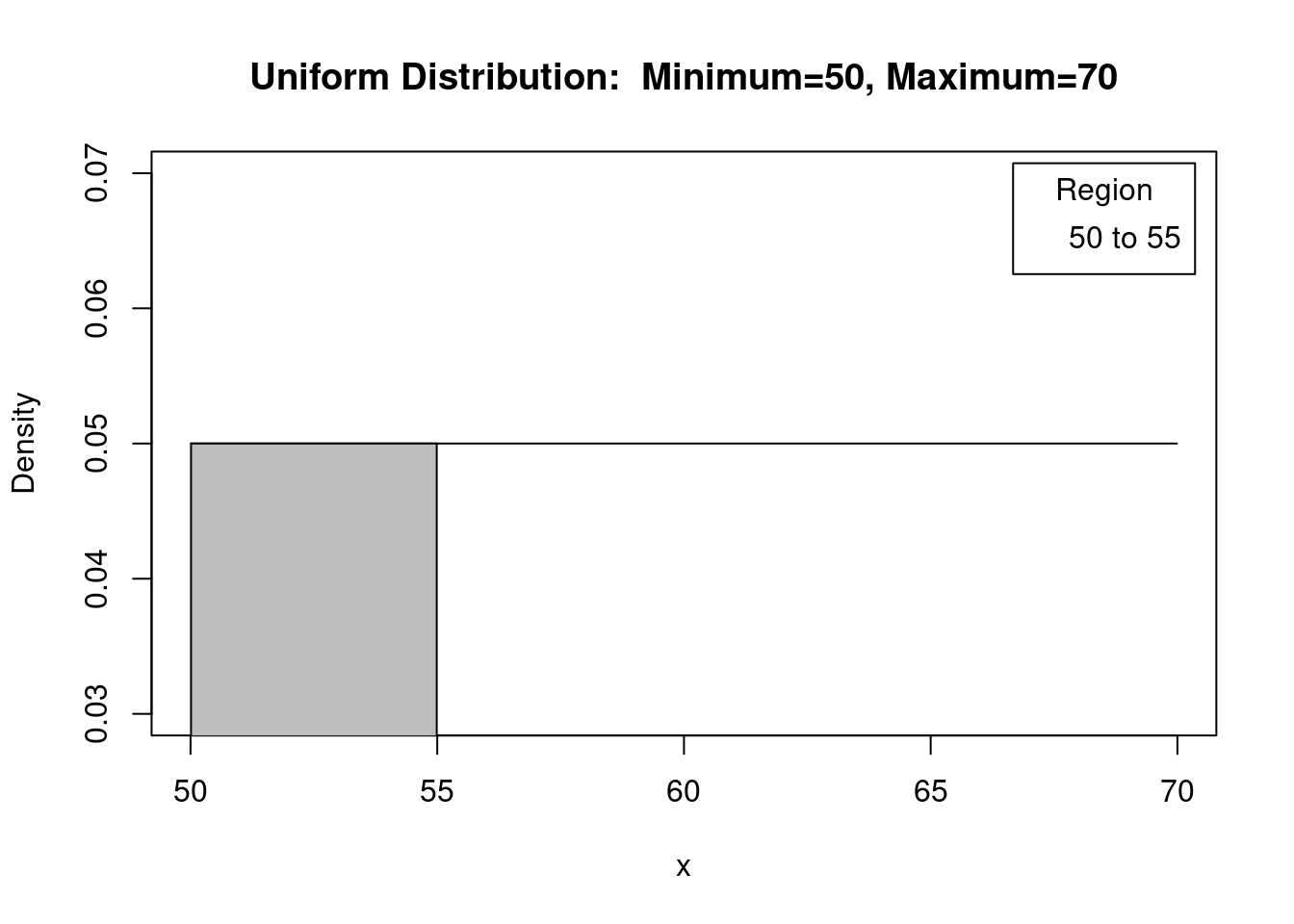
Figura 11.12: Gráfico da função de densidade de probabilidade para a distribuição uniforme com mínimo = 50 e máximo = 70. A área hachurada representa a probabilidade de se obter aleatoriamente um valor entre 50 e 55.

A probabilidade do exemplo 1 poderia também ser obtida a partir do R Commander por meio do item de menu Probabilidades da Uniforme (vide figura 11.9). Ao selecionarmos essa opção, a caixa de diálogo da figura 11.13 será exibida.

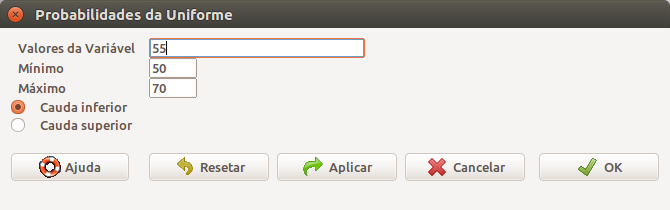
Figura 11.13: Caixa de diálogo para obtermos a probabilidade de selecionarmos aleatoriamente um valor entre 50 e 55 para a distribuição uniforme com mínimo = 50 e máximo = 70.

Fixando os valores mínimo e máximo, digitando 55 em Valores da Variável, selecionando a cauda inferior e pressionando o botão OK, obtemos a probabilidade desejada.

O valor esperado de uma distribuição uniforme com valores mínimo = \(a\) e máximo = \(b\) é:

\[\begin{align} E[X]=\frac{a+b}{2} \tag{11.6} \end{align}\]

ou seja, o ponto médio entre \(a\) e \(b\).

A variância de uma distribuição uniforme com valores mínimo = \(a\) e máximo = \(b\) é:

\[\begin{align} var(X)=\frac{(b-a)^2}{12} \tag{11.7} \end{align}\]

obtida por meio da resolução da integral \(\int_{a}^{b}\left(x-\frac{a+b}{2}\right)^2\frac{1}{b-a}dx\)

11.7 Distribuição normal ou gaussiana

O conteúdo desta seção pode ser visualizado neste vídeo.

A função densidade de probabilidade normal é a mais importante das distribuições contínuas, uma vez que possui vasta aplicação em modelagem e inferência estatística. Essa função tem uma forma de sino e sua equação é:

\[\begin{align} f(X) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{(X-\mu)}{\sigma})^2} \tag{11.8} \end{align}\]

Ela é abreviadamente representada como N(\(\mu\), \(\sigma\)²), onde os parâmetros \(\mu\) e \(\sigma\) são respectivamente o valor esperado, ou a média da distribuição, e o desvio padrão. A figura 11.14 mostra o gráfico da função densidade de probabilidade N(0,1), que é conhecida como distribuição normal padronizada ou distribuição normal padrão.

Figura 11.14: Gráfico da função densidade de probabilidade da distribuição normal padrão.

A figura 11.15 mostra os gráficos das funções densidade de probabilidade de duas distribuições normais, N(170, 16) e N (190, 16), que diferem somente no valor da média. A figura 11.16 mostra os gráficos das funções densidade de probabilidade de duas distribuições normais, N(170, 4) e N (170, 16), que diferem somente no valor do desvio padrão. Como é de se esperar, a média indica a localização da função densidade e o desvio padrão indica o quanto o gráfico se concentra em torno da média.

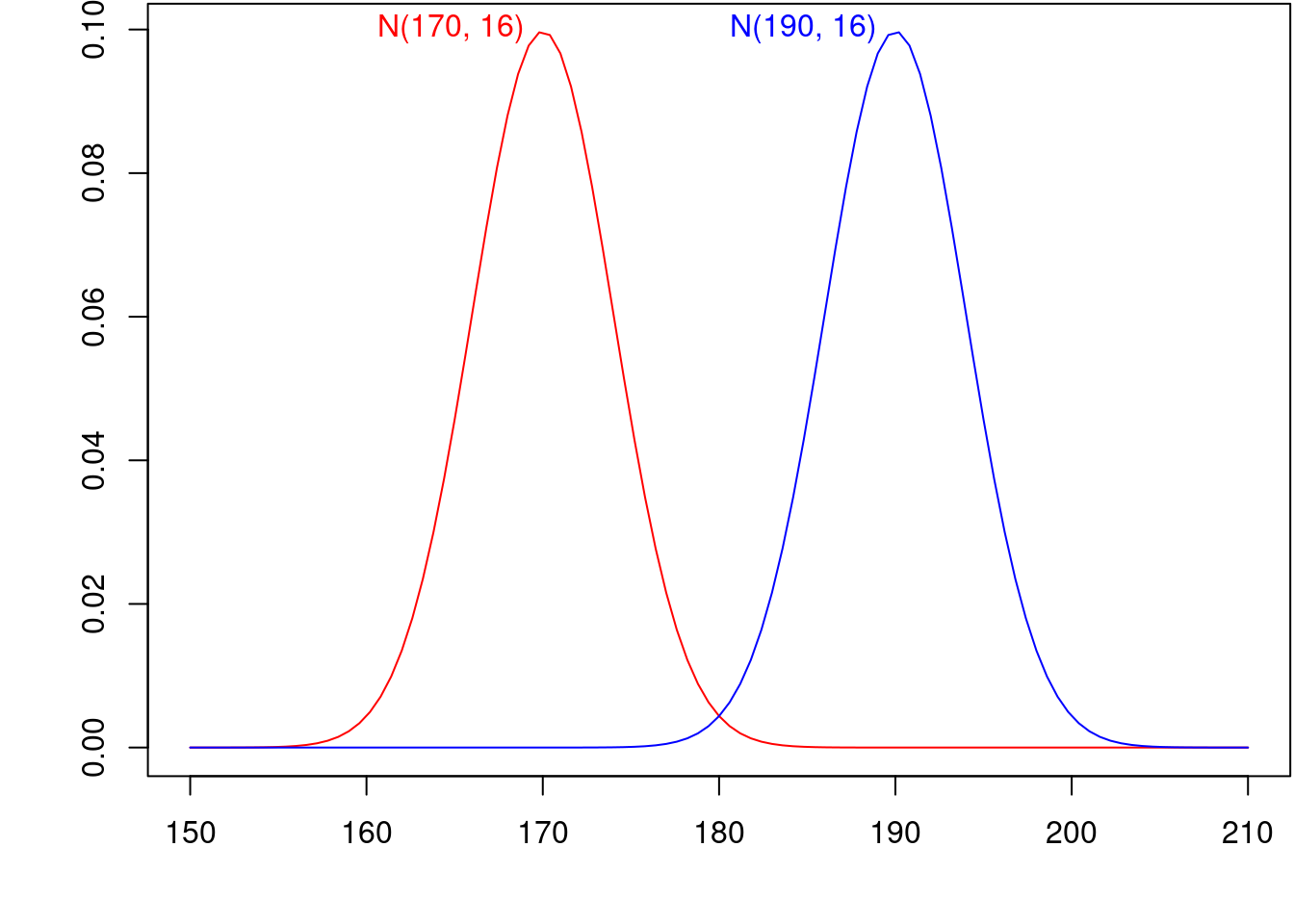
Figura 11.15: Gráfico da função densidade de probabilidade de duas distribuições normais que diferenciam somente no valor da média.

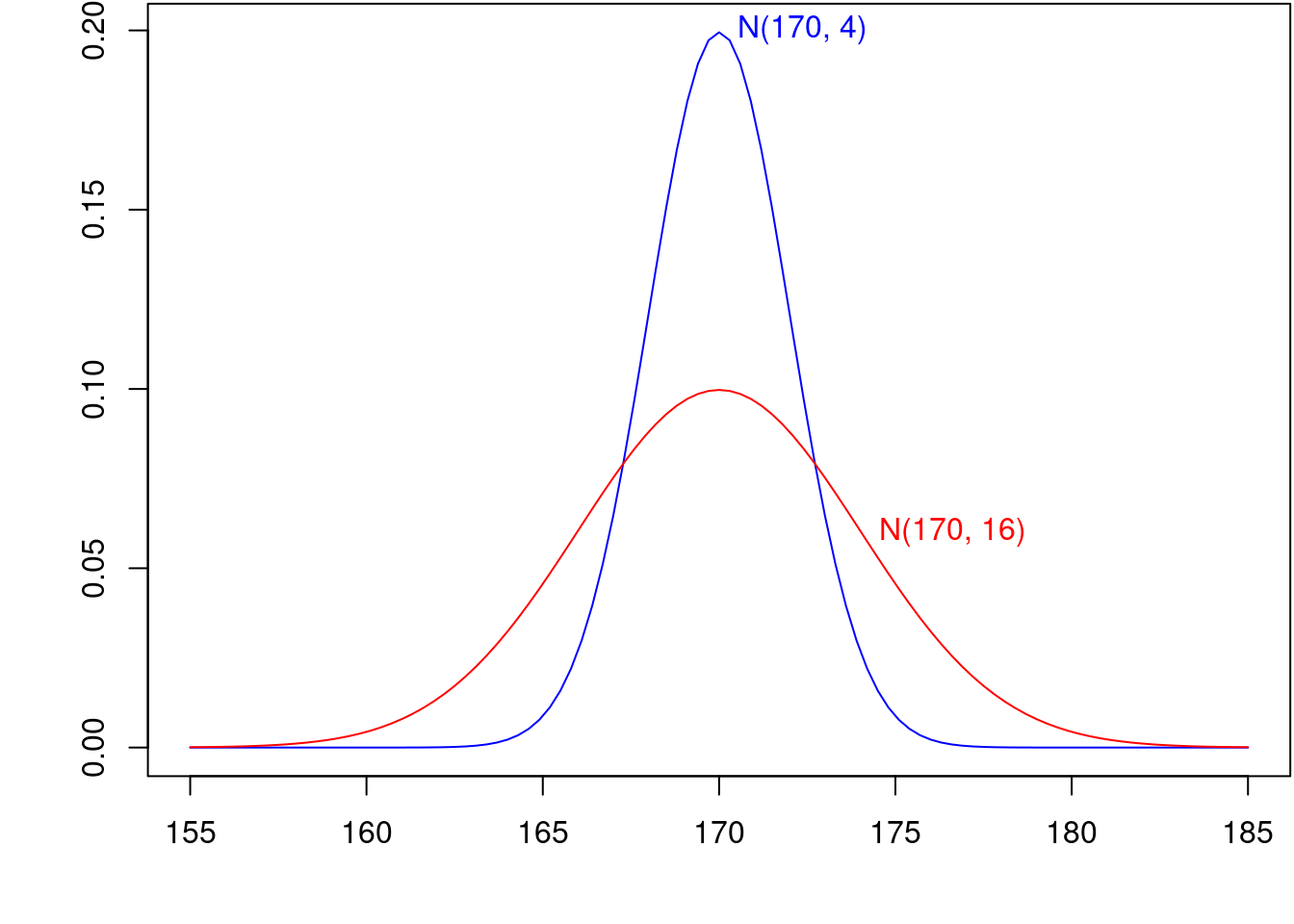
Figura 11.16: Gráfico da função densidade de probabilidade de duas distribuições normais que diferenciam somente no valor do desvio padrão.

Uma variável aleatória X com distribuição normal N(\(\mu\), \(\sigma\)²) pode ser convertida à normal padronizada Z, com distribuição N(0,1), usando a expressão:

\[\begin{align} Z = \frac{X-\mu}{\sigma} \tag{11.9} \end{align}\]

A transformação para a variável Z padronizada produz um número que expressa quantos desvios padrões o valor da variável original X está distante da média, ou seja, obtemos uma medida padronizada da distância do valor de X à média. Por exemplo, Z = 1, indica que o dado está a 1 desvio padrão da média, Z = 1,5 indica que o valor de X dista exatamente 1,5 desvios padrões da média e assim por diante.

A função normal não possui uma integral analítica, ou seja, se quisermos obter a probabilidade de X \(\le\) x₀ para uma N(\(\mu\), \(\sigma\)²), teríamos que resolver a integral:

\(\begin{aligned} f(x_0)=P(X\leq x_0) = \int_{-\infty}^{x_0}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx \end{aligned}\)

por métodos numéricos. Felizmente, podemos recorrer ao uso de tabelas onde a integral da N(0,1) para diferentes valores encontra-se tabulada ou, então, recorrer a um programa de computador como o R. O uso de tabelas requer alguns cuidados, fundamentalmente porque não há uma padronização de como os valores são tabelados. O R fornece, por meio da função pnorm, a área sob a curva da função densidade de probabilidade de uma variável aleatória com distribuição normal qualquer de \(-\infty\) até o valor x₀ de interesse especificando o parâmetro lower.tail = TRUE, ou de x₀ até \(+\infty\) especificando o parâmetro lower.tail = FALSE.

Exemplo 2: Uma população de homens tem altura com distribuição normal, \(\mu\) = 170 cm e \(\sigma\) = 4 cm, isto é, N(170, 16). Qual a probabilidade de que um indivíduo selecionado aleatoriamente dessa população tenha a altura entre 165 cm a 174 cm?

Estamos interessados em calcular P(165 \(\le\) X \(\le\) 174). Para calcularmos essa probabilidade, teríamos que calcular a área sob a função densidade de probabilidade da N(170, 16), situada entre 165 e 174. Para obtermos o gráfico da distribuição normal no R Commander, selecionamos a opção:

\[\text{Distribuições} \Rightarrow \text{Distribuições Contínuas} \Rightarrow \text{Dist. Normal} \Rightarrow \text{Gráfico dist. normal}\]

A figura 11.17 mostra como configurar os parâmetros da distribuição normal e selecionar a região que será preenchida (entre 165 e 174) e a figura 11.18 mostra o gráfico da função densidade de probabilidade e a área entre 165 e 174 cm.

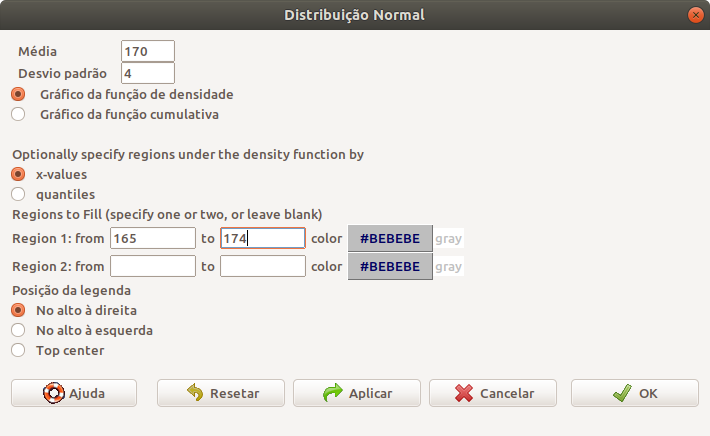
Figura 11.17: Caixa de diálogo para gerar um gráfico de uma distribuição normal. Especificando os limites de uma região, fará com que a área sob o gráfico entre esses limites seja preenchida.

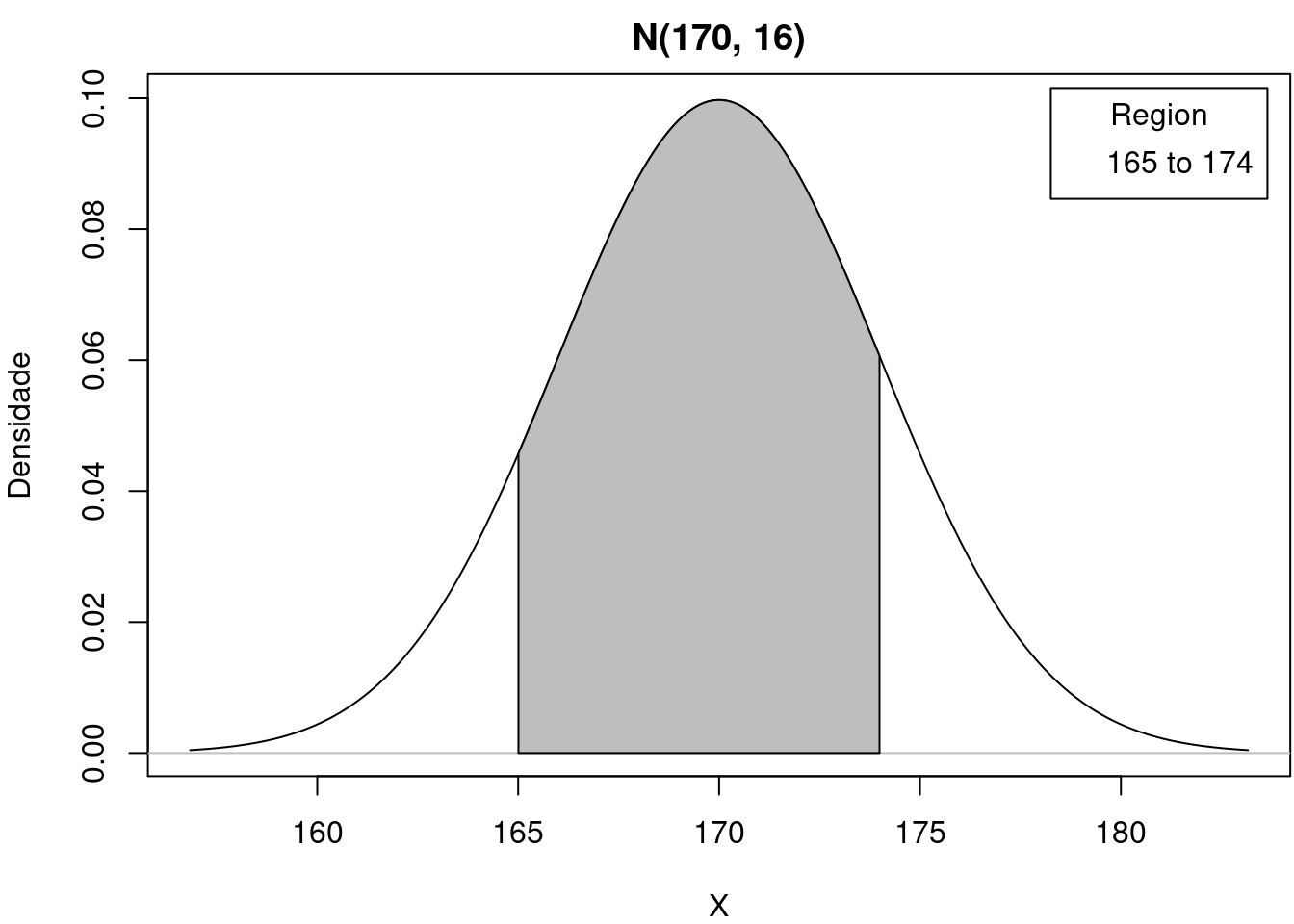
Figura 11.18: A área preenchida representa a probabilidade de se selecionar aleatoriamente um homem da população com altura entre 165 e 174 cm.

A área preenchida na figura 11.18, ou seja, a probabilidade de se selecionar aleatoriamente um indivíduo com altura entre 165 e 174, pode ser calculada por meio da área preenchida do gráfico à direita na figura 11.19 menos a área preenchida do gráfico à esquerda

\(P(165 \le X \le 174) = P(X \le 174) - P(X \le 165)\)

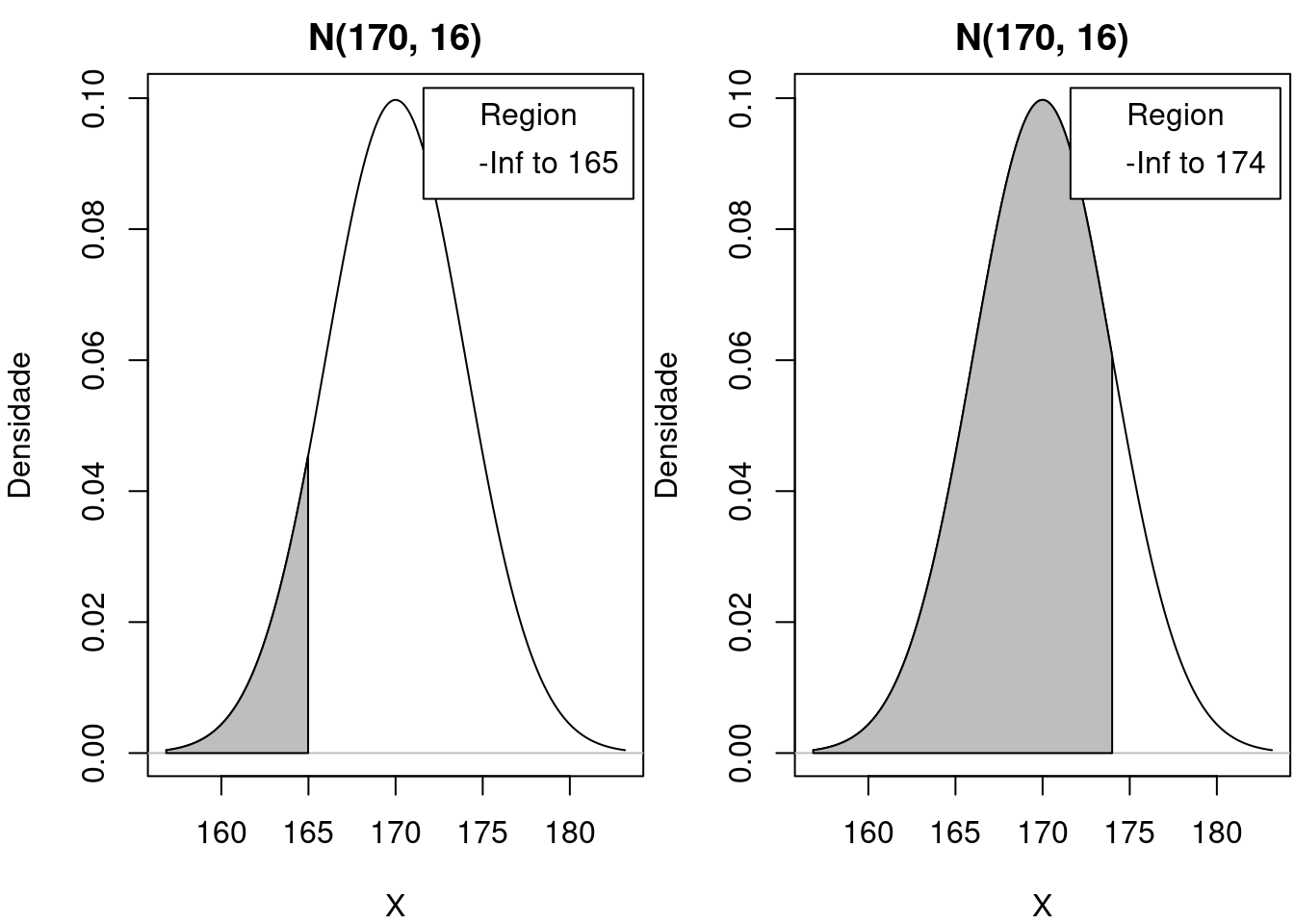
Figura 11.19: A área preenchida na figura 11.18 pode ser calculada por meio da área preenchida do gráfico à direita menos a área preenchida do gráfico à esquerda

As duas probabilidades P(X \(\le\) 174) e P(X \(\le\) 165) podem ser calculadas no R Commander por meio da opção:

\[\text{Distribuições} \Rightarrow \text{Distribuições Contínuas} \Rightarrow \text{Dist. Normal} \Rightarrow \text{Probabilidades da Normal...}\]

A figura 11.20 mostra como calcular a probabilidade P(X \(\le\) 174).

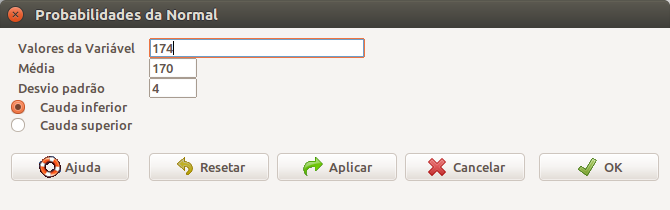
Figura 11.20: Caixa de diálogo para calcularmos a probabilidade P(X \(\le\) 174).

A função para calcular a probabilidade P(X \(\le\) 174) é dada a seguir:

pnorm(c(174), mean=170, sd=4, lower.tail=TRUE)

## [1] 0.8413447

Analogamente, obtemos P(X \(\le\) 165):

pnorm(c(165), mean=170, sd=4, lower.tail=TRUE)

## [1] 0.1056498

O comando abaixo calcula \(P(165 \le X \le 174) = P(X \le 174) - P(X \le 165)\):

pnorm(174, mean=170, sd=4, lower.tail=TRUE) - 
    pnorm(165, mean=170, sd=4, lower.tail=TRUE)

## [1] 0.735695

11.7.1 Valores importantes da variável Z padronizada

(Z1): Regra 68-95
A probabilidade de extrairmos um indivíduo da população e o valor observado da variável estar dentro do intervalo de um desvio padrão abaixo ou acima da média (isto é, entre -1 e 1 para a distribuição normal padrão) é 68% (0,6826). Similarmente, a probabilidade de extrairmos um indivíduo da população e o valor observado da variável estar dentro do intervalo de dois desvios padrões abaixo ou acima da média é 95% (0,9544).

(Z2): Quartis
Para uma curva normal padronizada (Z), o primeiro quartil é -0,67 e o terceiro quartil é 0,67. Ou seja, para uma variável aleatória com distribuição normal, é de 50% a probabilidade de extrairmos um indivíduo da população e o valor observado da variável estar dentro de 2/3 de desvios padrões em torno da média.

(Z3): Valores extremos (outliers)
Em um diagrama de boxplot no R, por padrão, outliers são valores que estão a mais de 1,5 vezes o intervalo ou faixa inter-quartilica (IQR), antes do Q1 (primeiro quartil) ou após o Q3 (terceiro quartil). Como conhecemos Q1 e Q3 para a normal, o IQR = 0,67 -(-0,67) = 1,34

Usando o valor acima, temos que valores extremos são aqueles menores do que -2,68 (-0,67 - 1,5 x 1,34) ou maiores do que 2,68 (0,67 + 1,5 x 1,34) desvios padrões. A probabilidade de se observar valores extremos é, portanto:

P(z < -2,68) + P(z > 2,68) =  0,0037 + 0,0037 = 0,0074, 

isto é, menor que 1%.

No R, para obtermos P(X < -x₀ ou X > x₀), com x₀ = 2,68, usamos a seguinte função:

pnorm(-2.68) + pnorm(2.68, lower.tail = FALSE)

## [1] 0.007362216

A função distribuição normal, que também é conhecida como gaussiana, tem sua importância em primeiro lugar, porque diversas medições físicas são aproximadas muito bem por essa distribuição. Por exemplo, se o erro de medição de uma quantidade desconhecida é o resultado da soma de diversos pequenos erros que podem ser positivos ou negativos e que ocorrem aleatoriamente, então a distribuição normal pode ser utilizada para modelar esse erro.

Outro aspecto é que diversas variáveis aleatórias que não são normalmente distribuídas podem ser transformadas, por exemplo tomando o logaritmo ou a raiz quadrada da variável de interesse, e o resultado da transformação pode ser aproximadamente normalmente distribuído.

11.7.2 Aproximação da distribuição binomial pela normal

Em muitas situações, podemos aproximar a distribuição binomial, que é uma distribuição discreta pela distribuição normal. Essa aproximação é adequada quando, no modelo B(n,p), n é grande e p não está muito próximo de 0 ou 1. Por exemplo, para n > 20 e 0,3 < p < 0,7, temos uma boa aproximação. Outros autores consideram que a aproximação é boa para np > 5 e n(1-p) > 5. A vantagem de usarmos essa aproximação é que, para problemas com n grande, o cálculo das probabilidades da binomial é trabalhoso, caso sejam feitos manualmente. Atualmente, com o uso de computadores, essa dificuldade foi minimizada mas, mesmo assim, em diversas situações, a aproximação é útil.

Para usarmos a aproximação normal para a binomial, fazemos \(\mu = np\) e \(\sigma\)² = np(1-p), que são justamente a média e a variância da binomial. A figura 11.21 ilustra a aplicação Binomial x Normal, que mostra um gráfico da distribuição normal sobreposto ao gráfico da binomial para diferentes combinações de n e p. Observem que, para n = 12 e p = 0,1, a aproximação não é boa. Já para n = 10 e p = 0,5 (figura 11.22), a aproximação parece bastante razoável. Vamos utilizar essa aproximação para calcularmos probabilidades da binomial, usando a distribuição normal.

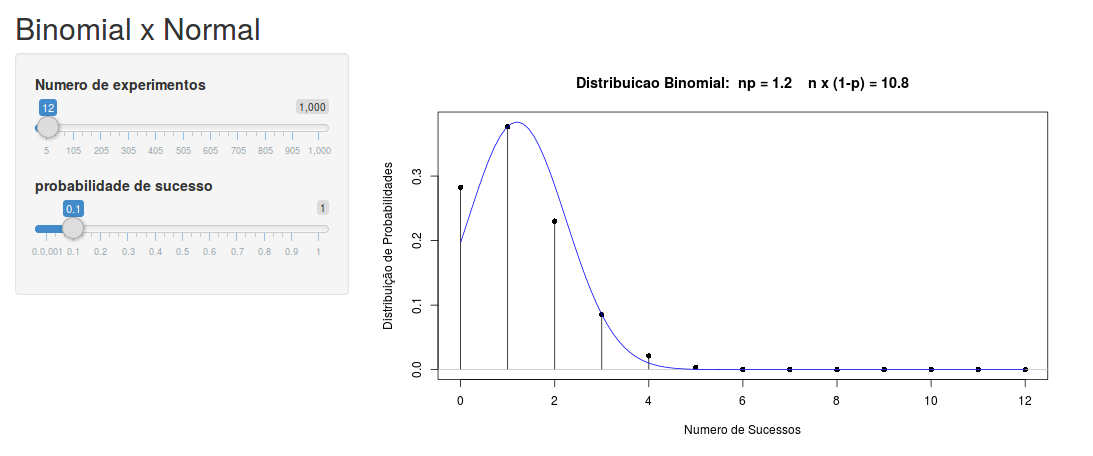
Figura 11.21: Aplicação para verificar a relação entre a distribuição normal e a distribuição binomial.

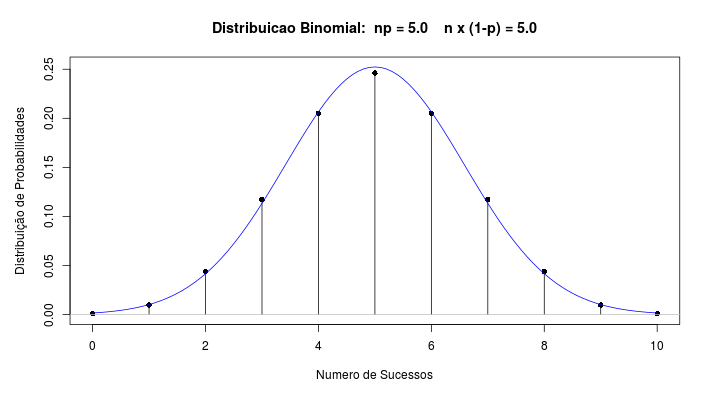
Figura 11.22: Gráficos das distribuições N(5, 2,5) e B(10, 0,5). A aproximação usando a normal parece bastante razoável.

Vamos calcular a probabilidade de obtermos um número de sucessos entre 5 e 8 (P(5 \(\le\) X \(\le\) 8)) para a distribuição binomial B(12; 0,5). Usando o R Commander, conforme visto no capítulo anterior, podemos calcular essa probabilidade, usando o comando a seguir:

pbinom(8, size=12, prob=0.5,lower.tail=TRUE) -
    pbinom(4, size=12, prob=0.5,lower.tail=TRUE)

## [1] 0.7331543

Usando uma aproximação normal para essa distribuição binomial, N(6, 3), poderíamos pensar em calcular a área sob a função densidade da normal, compreendida entre 5 e 8 (figura 11.23).

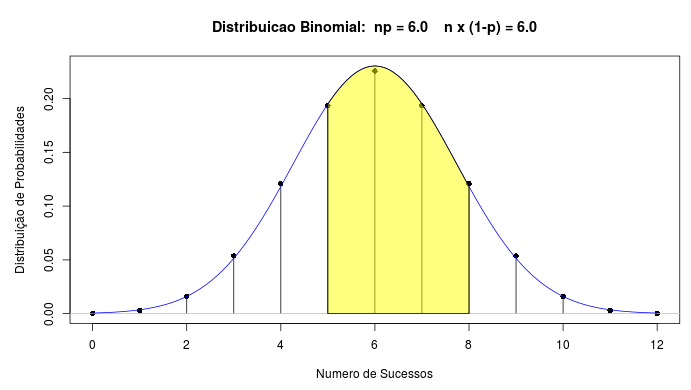
Figura 11.23: Gráficos das distribuições N(6, 3) e B(12, 0,5). A área em amarelo representa a área sob o gráfico da distribuição normal entre 5 e 8.

A área em amarelo na figura 11.23 pode ser calculada por meio da expressão abaixo:

pnorm(8, mean=6, sd=1.732, lower.tail=TRUE) -
    pnorm(5, mean=6, sd=1.732, lower.tail=TRUE)

## [1] 0.5940547

O resultado P(5 \(\le\) X \(\le\) 8) = 0,594 é bastante diferente do valor real (0,733), obtido anteriormente. Devemos ter em mente, porém, que a função densidade de probabilidade da distribuição normal é uma função contínua e, para obtermos as probabilidades da binomial, devemos realizar uma correção de continuidade. Para esse exemplo, essa correção implica em calcularmos a área entre 4,5 e 8,5 (figura 11.24).

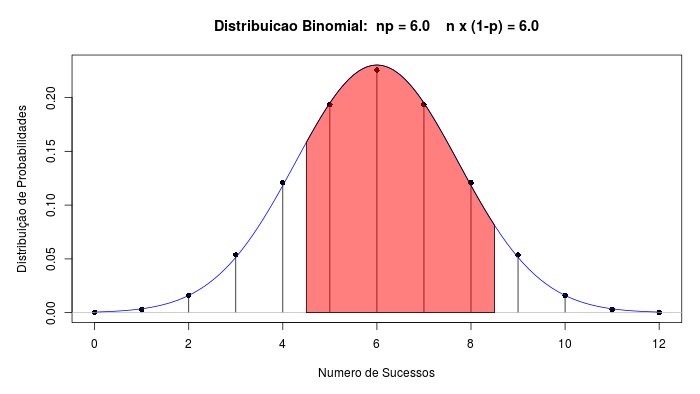
Figura 11.24: Gráficos das distribuições N(6, 3) e B(12, 0,5). A área em vermelho representa a área sob o gráfico da distribuição normal entre 4,5 e 8,5.

Para calcular P(4,5 \(\le\) X \(\le\) 8,5), usamos o comando a seguir:

pnorm(8.5, mean=6, sd=1.732, lower.tail=TRUE) -
    pnorm(4.5, mean=6, sd=1.732, lower.tail=TRUE)

## [1] 0.7323175

O resultado, P(4,5 \(\le\) X \(\le\) 8,5) = 0,732, é bastante próximo do valor real.

Assim, ao aproximarmos a distribuição binomial pela normal, devemos aplicar correções de continuidade. Que tipo de correção você aplicaria para calcular P(X \(\le\) 5) para a distribuição B(12; 0,5)? E para calcular P(X \(\ge\) 8)? E para calcular P(X < 5)? E para calcular P(X > 8)? E para calcular P(X = 8)?

11.7.3 Aproximação da distribuição de Poisson pela normal

A distribuição de Poisson também pode ser aproximada pela distribuição normal para valores suficientemente grandes do parâmetro \(\lambda\). A figura 11.25 ilustra a aplicação Poisson x Normal, que mostra um gráfico da distribuição normal sobreposto ao gráfico da distribuição de Poisson para diferentes valores de \(\lambda\). A média e a variância da distribuição normal são iguais a \(\lambda\). Observem que, para \(\lambda\) = 2, a aproximação não é boa (figura 11.26). Já para \(\lambda\) = 15 (figura 11.27), a aproximação melhora bastante. Podemos adotar este critério: a partir de \(\lambda\) = 15, a distribuição normal com média e variância iguais a \(\lambda\) é uma boa aproximação para a distribuição de Poisson com parâmetro \(\lambda\). Ao calcularmos probabilidades usando essa aproximação, também devemos adotar a correção de continuidade, analogamente ao caso da distribuição binomial.

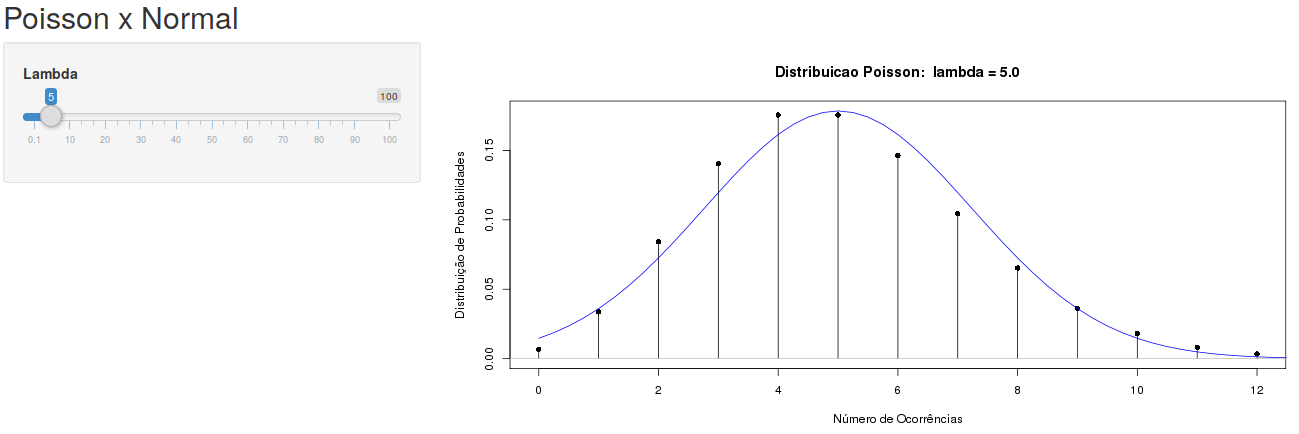
Figura 11.25: Aplicação para verificar a relação entre a distribuição normal e a distribuição de Poisson.

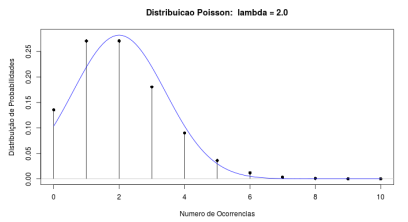
Figura 11.26: Gráficos das distribuições Pois(2) e N(2, 4). A aproximação da normal não é boa.

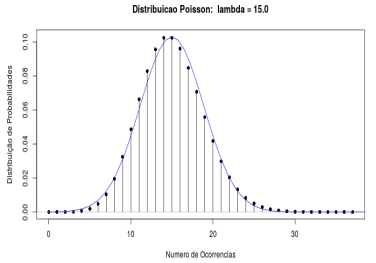
Figura 11.27: Gráficos das distribuições Pois(15) e N(15, 15). A aproximação da normal parece bastante razoável.

11.8 Distribuição exponencial

Uma variável aleatória contínua X possui uma distribuição exponencial com parâmetro \(\lambda\) quando a sua função densidade de probabilidade for dada por:

\[\begin{align} \begin{split} f(X) = \begin{cases} \lambda e^{-\lambda X},\ se\ X > 0 \\ 0,\ \text{caso contrário} \end{cases} \end{split} \tag{11.10} \end{align}\]

Essa é uma distribuição importante, utilizada para estudos que envolvem o intervalo de tempo entre eventos. Está intimamente associada à variável aleatória de Poisson, que estuda o número de eventos que ocorrem em um dado intervalo de tempo. O parâmetro \(\lambda\) corresponde à taxa média de eventos na unidade de tempo (ou distância, ou outra unidade de interesse).

A figura 11.28 mostra gráficos da função exponencial para três valores diferentes do parâmetro \(\lambda\). Cada um dos gráficos pode ser obtido a partir do R Commander, acessando a caixa de diálogo para obter o gráfico de uma distribuição exponencial a partir do menu mostrado na figura 11.9.

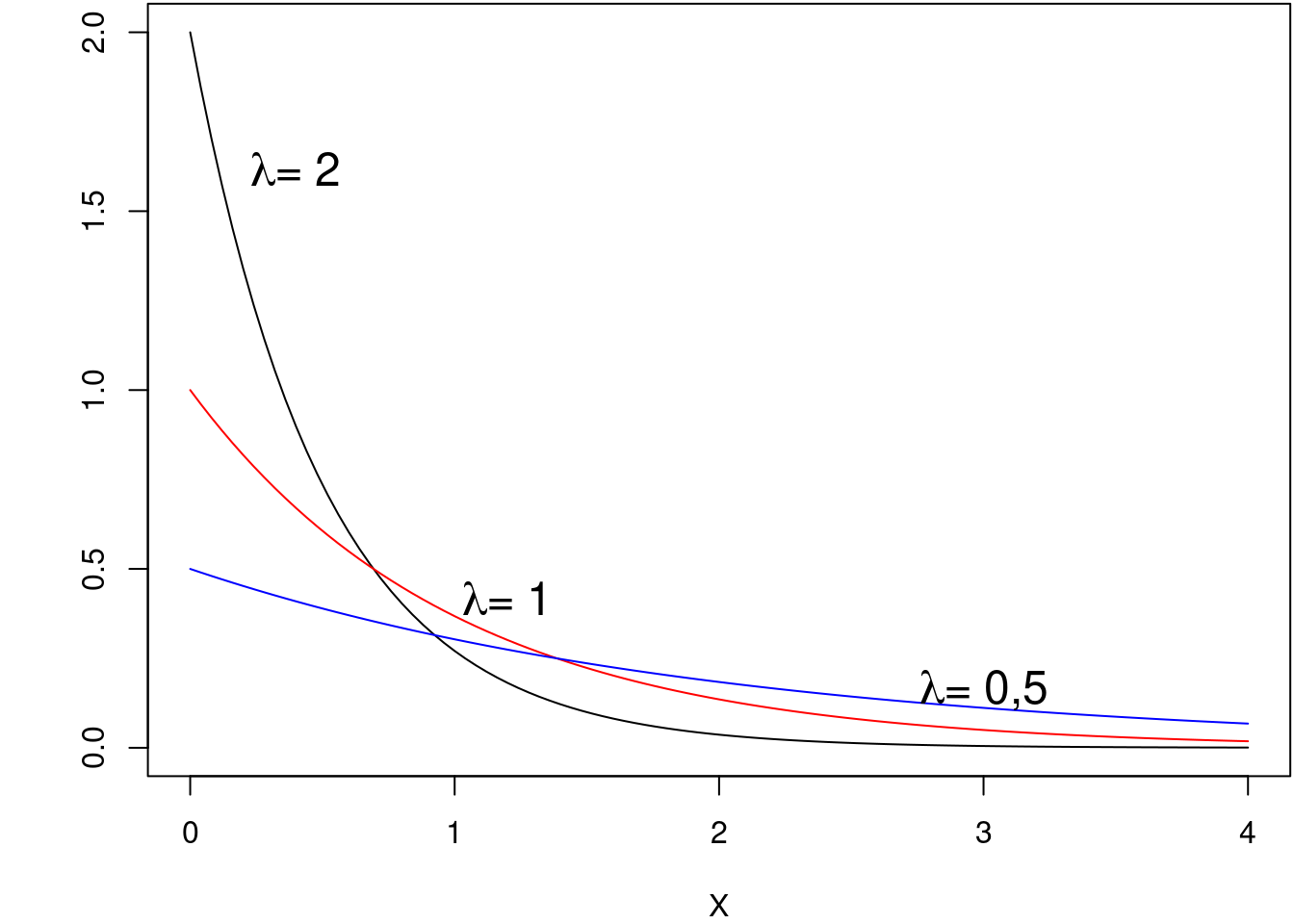
Figura 11.28: Gráficos da função de densidade de uma distribuição exponencial para \(\lambda\) = 0,5; 1 e 2, respectivamente.

O valor esperado e a variância da distribuição exponencial são dados por:

\[\begin{align} E[X] =\int_{0}^{\infty}x\lambda e^{-\lambda x}dx = \frac{1}{\lambda} \tag{11.11} \end{align}\]

\[\begin{align} var(X) =\int_{0}^{\infty}\left(x-\frac{1}{\lambda}\right)^2\lambda e^{-\lambda x}dx=\frac{1}{\lambda^2} \tag{11.12} \end{align}\]

Logo a variância de uma variável aleatória com distribuição exponencial é igual ao quadrado da média.

A função de distribuição cumulativa da distribuição exponencial é facilmente obtida. Seja T uma variável aleatória com distribuição exponencial e parâmetro \(\lambda\). Se t > 0, então temos:

\(\begin{aligned} \ F(t) = P(T\leq t) = \int_{0}^{t}\lambda e^{-\lambda x}dx = 1-e^{-\lambda t} \end{aligned}\)

Uma propriedade importante da função densidade exponencial é que ela não possui “memória”, ou seja:

\(\begin{aligned} \ P(T >r + s|T>r) = P(T>s) \end{aligned}\)

ou seja, a probabilidade condicional do evento “encontrarmos um intervalo de tempo maior que a soma de dois intervalos r+s, dado que o intervalo de tempo é maior do que a primeira parcela da soma” é independente dessa parcela. Essa propriedade pode ser demonstrada, notando que

\(P(T > s) = 1 - P(T \le s) = 1 - F(s) = e^{-\lambda s}\)

\(P(T > r + s|T >r) = \frac{P(T > r+s\ e\ T>s)}{P(T > r)} = \frac{P(T > r+s)}{P(T > r)}\)

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \frac{1-F(r+s)}{1-F(r)}\)

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \frac{e^{-\lambda(r+s)}}{e^{-\lambda r}} = e^{-\lambda s}\)

Existe uma relação importante entre a distribuição de Poisson e a função densidade exponencial. Para a distribuição de Poisson, consideramos o número de eventos em um dado intervalo t. Se os eventos ocorrem a uma taxa de \(\lambda\) eventos por unidade de tempo, então a média da distribuição de Poisson será \(\mu = \lambda t\). Lembrando da expressão da distribuição de Poisson, podemos estimar qual é a probabilidade de termos zero eventos em um dado intervalo t, isto é,

\(\begin{aligned} \ P(X=0) = Pois(\lambda t) = \frac{ e^{-\lambda t}(\lambda t)^0}{0!} = e^{-\lambda t} \end{aligned}\)

Se agora considerarmos a variável aleatória T, correspondente ao tempo entre um instante genérico e o instante em que o evento ocorre, esse valor será maior que um dado t, desde que não ocorra nenhum evento até esse ponto, isto é, ele será igual a P(X = 0) acima:

\(\begin{aligned} \ P(T>t) = e^{-\lambda t} \end{aligned}\)

Logo teremos

\(\begin{aligned} \ P(T\leq t) = 1-e^{-\lambda t} \end{aligned}\)

que nada mais é do que a função distribuição cumulativa da exponencial. Concluindo, para um processo de Poisson, o intervalo entre eventos segue uma distribuição exponencial.

Exemplo 3: Se o tempo de vida médio de um componente eletrônico é igual a 100 horas, temos que a taxa de falhas por hora será \(\lambda\)= 1/100. Supondo que o tempo de vida desse componente possua uma distribuição exponencial, para obtermos a probabilidade de que o componente falhe antes de 50 horas, temos que usar a função distribuição de probabilidade (que é a cumulativa)

F(x) = 1 - e^{-\(\lambda\)t} , com t = 50.

Logo obtemos para a probabilidade desejada

P(T \(\le\) 50) = F(50) = 1 - e^-50/100 = 0,393

11.9 Transformação de variáveis e variáveis independentes

Sejam X e Y duas variáveis aleatórias contínuas, tal que \(Y = aX + b\), onde \(a\) e \(b\) são números reais quaisquer, ou seja, Y é uma transformação linear de X. Analogamente ao caso das variáveis aleatórias discretas, para variáveis contínuas, ao realizarmos uma transformação linear de variáveis, as seguintes fórmulas para o valor esperado e variância se aplicam:

\[\begin{align} E[Y] &= aE[X] + b \tag{11.13} \\ var(Y) &= a^2 var(X) \tag{11.14} \end{align}\]

Sejam X e Y duas variáveis aleatórias independentes e Z uma variável aleatória, tal que:

\(Z = X + Y\)

Então:

\[\begin{align} E[Z] &= E[X] + E[Y] \tag{11.15} \\ var(Z) &= var(X) + var(Y) \tag{11.16} \end{align}\]

Esses resultados se estendem para uma soma de n variáveis independentes.

Em particular, se X e Y são normalmente distribuídas, com distribuição \(N(\mu, \sigma^2)\), então Z também será normalmente distribuída com distribuição \(N(2\mu, 2\sigma^2)\).

Exemplo 4: Dadas n variáveis aleatórias independentes X₁, X₂, …, X_n obtidas de uma distribuição normal N( \(\mu\), \(\sigma\)²), obter o valor esperado e a variância das novas variáveis:

\(\begin{aligned} &\ S_n = X_1 + X_2 + \dots + X_n \\ &\ T_n = \frac{S_n}{n} \end{aligned}\)

Solução: Como S_n é uma soma de n variáveis independentes com a mesma distribuição normal, então ela terá uma distribuição normal cuja média é \(n\mu\) e cuja variância é \(n\sigma^2\). Logo:

\(\begin{aligned} &\ \boldsymbol{S_n \sim N(n\mu, n\sigma^2)}. \end{aligned}\)

Como T_n é uma transformação linear de S_n, podemos aplicar as fórmulas (11.13) e (11.14), estendendo-as para n variáveis. Logo:

\(\begin{aligned} &\ \text{média de } T_n = \frac{1}{n}E[S_n] = \frac{n\mu}{n} = \mu \\ &\ \text{variância de } T_n = \frac{1}{n^2}var(S_n) = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n} \end{aligned}\)

Portanto T_n possui a mesma média de cada uma das parcelas da soma, porém a sua variância é a variância de uma das parcelas dividida por n. T_n possui uma dispersão menor do que cada uma das parcelas, para n > 1. Iremos discutir esse resultado com mais detalhes no capítulo 13.

Como S_n é normalmente distribuída, então:

\(\begin{aligned} &\ \boldsymbol{T_n \sim N(\mu, \sigma^2/n)}. \end{aligned}\)

Concluindo este tópico sobre distribuições de probabilidades, ressaltamos que há ainda um número grande de outras distribuições que não foram abordadas aqui. Algumas, como a t de Student e qui ao quadrado serão abordadas mais adiante quando forem apresentados os conceitos de intervalo de confiança e testes de hipóteses.

11.10 Exercícios

1. Numa distribuição de probabilidades para uma variável aleatória discreta, é possível saber a probabilidade para cada valor da variável aleatória. E para uma variável contínua, qual é a probabilidade de se obter um valor particular da variável aleatória?

2. Em relação à resposta anterior, como conciliar a sua resposta com o fato de que se você extrair uma amostra de uma população, você vai obter um conjunto de valores para a variável aleatória que você está interessado?

3. Como você traça o gráfico da função densidade de probabilidade

    f(x) = { 0.1 – 0.005x, onde 0 < x < 20 

   Qual é a área compreendida entre o gráfico dessa função e o eixo X?

4. Suponha que a temperatura em um certo local seja normalmente distribuída com média 50º e variância 4. Indique, usando a curva normal como você calcularia a probabilidade de que a temperatura T em um dado dia esteja entre 48º e 53º C? E a probabilidade de que a temperatura T esteja acima de 53º C ou abaixo de 44º C?

5. Vamos supor que a pressão arterial sistólica dos membros de uma certa sociedade acadêmica siga uma distribuição normal com média igua a 125 mmHg e o desvio padrão igual a 10 mmHg.

   1. Qual a variância dessa população?
   2. Qual a probabilidade de selecionarmos aleatoriamente um membro dessa população e obtermos o valor de 125 mmHg exatamente para a pressão sistólica?
   3. É possível extrairmos uma amostra de 10 pessoas e obtermos um valor da média de pressão sistólica acima de 140 mmHg? Explique a resposta.