16 Comparação de médias entre dois grupos
16.1 Introdução
O conteúdo desta seção pode ser visualizado neste vídeo.
Este capítulo discute técnicas para estudar a relação entre uma variável binária e uma variável quantitativa. Vamos considerar duas situações distintas.
A primeira situação diz respeito à estimativa da diferença das médias dos valores de uma variável numérica em dois grupos distintos de pacientes. O estudo de Haijanen et al. (Haijanen et al. 2019) foi um ensaio controlado randomizado multicêntrico que fez uma comparação de custos de antibióticos x apendectomia para o tratamento da apendicite aguda sem complicações. Parte dos resultados estão mostrados na figura 16.1. Por exemplo, para custos hospitalares em 5 anos de acompanhamento, os autores apresentaram o custo médio para cada grupo de tratamento (2730 x 2056 euros), bem como a diferença de custos entre os dois grupos (674). Ao lado de cada custo, foram mostrados entre parênteses o intervalo de confiança ao nível de 95%. Na última coluna, os autores apresentaram os valores de p resultante dos testes de hipóteses para verificar a significância estatística da diferença entre os custos de cada tratamento.
A análise estatística para a diferença entre os custos médios nos dois grupos de tratamento foi baseada no teste t de Student. Diferenças entre os grupos em relação ao tempo de internação e licença médica (não apresentadas na tabela) foram testadas por meio do teste de Mann-Whitney.
Os dois grupos de pacientes nesse estudo são chamados independentes, porque as unidades de observação (os pacientes) foram alocados aos grupos de maneira independente. Em um arquivo de dados, usualmente uma variável binária é usada para designar o grupo a que cada unidade de análise pertence e outra variável designa a variável numérica que está sendo medida em cada unidade de análise (vide figura 1.9).
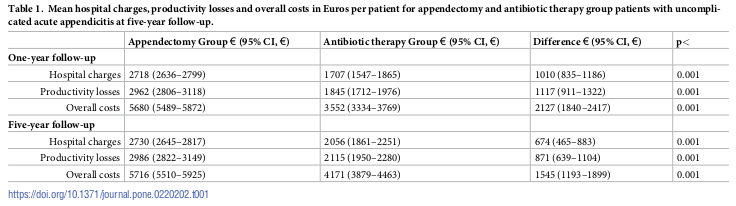
Figura 16.1: Comparação de diversos custos entre dois tratamentos para apendicite aguda. Fonte: tabela 1 do estudo de (Haijanen et al. 2019) (CC BY).
Outra situação é quando as duas amostras ou os dois grupos são dependentes. Isso pode ocorrer nos cenários apresentados a seguir.
O primeiro cenário diz respeito à estimativa da diferença de efeitos sobre uma variável numérica em um grupo de pacientes quando dois tratamentos distintos são aplicados em sequência aos pacientes (a ordem de aplicação pode ser aleatória) e, então, uma variável numérica é medida após cada tratamento e os valores da variável após cada tratamento são comparados. Cada conjunto de medidas da variável após cada tipo de tratamento forma um grupo.
Outro cenário é quando uma variável numérica é medida em cada par de indivíduos, sendo que cada par é formado por indivíduos semelhantes de acordo com algum critério estabelecido. Os primeiros elementos de cada par formam um grupo e os segundos elementos de cada par formam o outro grupo.
Um terceiro cenário é quando uma variável numérica é medida em dois instantes diferentes, ou em posições diferentes, em um mesmo grupo de indivíduos e os valores dessa variável nos dois instantes (posições) são comparados. Cada instante, ou cada posição, representa um grupo de medidas.
Por exemplo, o estudo de Andrade et al. (V. G. Andrade et al. 2018) avaliou o modelo de avaliação da homeostase do índice de resistência à insulina (HOMA-IR) em pacientes com hepatite C crônica tratados com medicação antiviral de ação direta na resposta virológica sustentada (RVS). Os dados foram coletados no início do tratamento (t-base) e na décima segunda semana após o término do tratamento (t-RVS12). O HOMA-IR foi calculado como insulinemia de jejum (\(\mu U/mL\)) x glicemia de jejum (mmol/L) / 22,5. A tabela 4 desse estudo (figura 16.2) mostra as médias das diferenças dos valores das variáveis glicemia de jejum, insulinemia de jejum e HOMA-IR entre o início do tratamento e a décima segunda semana após o término do tratamento para pacientes não diabéticos e com valores de HOMA-IR > 2,5. Foi realizado o teste t pareado para cada uma dessas médias e os valores de p dos testes são mostrados na última coluna da tabela.

Figura 16.2: Comparação dos valores das variáveis glicemia de jejum, insulinemia de jejum e HOMA-IR entre o início do tratamento e a décima segunda semana após o término do tratamento para pacientes não diabéticos e com valores de HOMA-IR > 2,5. Fonte: tabela 4 do estudo de (V. G. Andrade et al. 2018) (CC BY-NC).
Nos três cenários acima, dizemos que os grupos são dependentes, ou pareados, porque os valores da variável numérica tendem a estar correlacionados em cada indivíduo ou em cada par de indivíduos. Por exemplo, no estudo de Andrade et al., indivíduos que possuem valores de glicemia de jejum mais baixos antes do tratamento tendem a ter valores mais baixos de glicemia de jejum após o tratamento do que indivíduos que possuem valores mais altos de glicemia de jejum antes do tratamento.
Em amostras dependentes, há duas variantes para a organização do arquivo de dados. Numa variante, uma variável identifica cada indivíduo, uma segunda variável identifica os grupos (instante ou posição da medida, um dos elementos de cada par de indivíduos, ou tratamento aplicado) e uma variável numérica identifica o desfecho. Na segunda variante, duas variáveis numéricas identificam as duas medidas da variável (uma para um instante - posição da medida, um dos elementos de cada par de indivíduos ou um dos tratamentos aplicados - e outra para o outro instante - posição, elemento do par ou tratamento) (vide figura 1.10). Este capítulo discute as condições para a realização de cada uma das técnicas de análise indicadas acima, começando pela situação onde os dois grupos, ou amostras, são independentes.
16.2 Comparação de médias de amostras independentes
O conteúdo desta seção e da seção 16.2.1 podem ser visualizados neste vídeo.
Vamos utilizar o conjunto de dados energy da biblioteca ISwR (GPL-2 | GPL-3). Esse conjunto de dados contém o consumo de energia de 22 pessoas, sendo 13 magras e 9 obesas. As duas variáveis são: expend, que representa o consumo de energia, e stature, que indica se a pessoa é magra ou obesa. Para ler esse conjunto de dados, podemos utilizar o R Commander, seguindo o procedimento mostrado no capítulo 3, seção 3.6.1, ou por meio dos comandos:
## expend stature
## 1 9.21 obese
## 2 7.53 lean
## 3 7.48 lean
## 4 8.08 lean
## 5 8.09 lean
## 6 10.15 lean
## 7 8.40 lean
## 8 10.88 lean
## 9 6.13 lean
## 10 7.90 lean
## 11 11.51 obese
## 12 12.79 obese
## 13 7.05 lean
## 14 11.85 obese
## 15 9.97 obese
## 16 7.48 lean
## 17 8.79 obese
## 18 9.69 obese
## 19 9.68 obese
## 20 7.58 lean
## 21 9.19 obese
## 22 8.11 leanA primeira função carrega a biblioteca ISwR e a segunda função carrega o conjunto de dados energy. A última função mostra os dados das 22 pessoas.
Em relação ao conjunto de dados energy, podemos realizar as seguintes perguntas:
Existe alguma relação entre o consumo de energia e o fato de a pessoa ser magra ou obesa? Colocados em termos estatísticos, existe diferença estatisticamente significativa entre os níveis de consumo de energia entre pessoas magras e obesas?
Como podemos quantificar o valor e a precisão dessa diferença?
A figura 16.3 mostra os boxplots da variável expend para as mulheres magras e obesas respectivamente. Os diagramas sugerem que os consumos de energia, em geral, são maiores nas mulheres obesas do que nas mulheres magras. Vamos analisar esses dados estatisticamente.
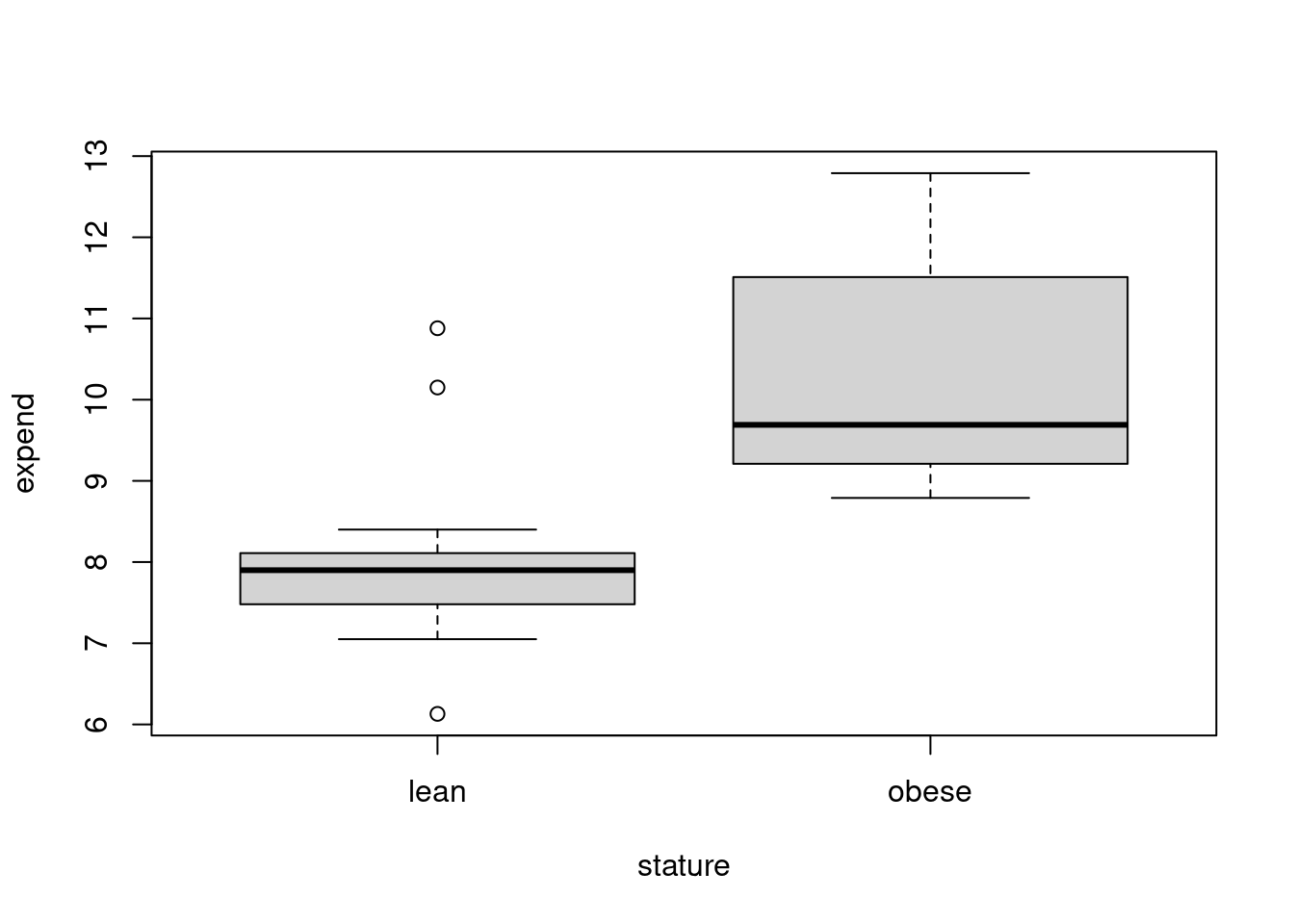
Figura 16.3: Boxplots da variável expend do conjunto de dados energy para as mulheres magras e obesas respectivamente.
De um modo geral, consideremos o seguinte problema: dadas duas populações, 1 e 2, que se distinguem por uma característica (por exemplo, magros e obesos), uma amostra de tamanho n1 é extraída aleatoriamente da população 1 e uma amostra aleatória de tamanho n2 é extraída da população 2. Sejam X1 a variável de interesse (por exemplo, consumo de energia), medida em cada unidade da amostra 1 e X2 a mesma variável medida nas unidades da amostra 2.
Vamos supor que:
\(X_1 \sim N(\mu_1, \sigma_1^2)\) e \(X_2 \sim N(\mu_2, \sigma_2^2)\)
e que as variâncias \(\sigma_1^2\) e \(\sigma_2^2\) sejam conhecidas.
Como X1 e X2 são variáveis aleatórias independentes, vimos na seção 9.6 que a variável
\(X = X_1 - X_2\)
terá uma distribuição \(N(\mu_1-\mu_2, \sigma_1^2+\sigma_2^2)\).
Consequentemente, a partir dos resultados da mesma seção 9.6, a diferença de médias amostrais
\(\bar{X} = \bar{X_1} - \bar{X_2}\)
terá uma distribuição \(N(\mu_1 - \mu_2, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2})\).
Vamos considerar diferentes situações.
Quando as variâncias \(\sigma_1^2\) e \(\sigma_2^2\) são conhecidas, a estatística
\(\begin{aligned} &\ Z = \frac{(\bar{X_1}- \bar{X_2}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \end{aligned}\)
possui uma distribuição normal padrão (vide capítulo 14, seção 14.2). A estatística
\[\begin{align} &\ \frac{\bar{X_1}- \bar{X_2}}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}\tag{16.1} \end{align}\]
pode ser utilizada para realizar um teste de hipótese bilateral para \(H_0: \mu_1 - \mu_2 = 0\) ou testes unilaterais para \(H_0: \mu_1 - \mu_2 \ge 0\) ou \(H_0: \mu_1 - \mu_2 \le 0\).
O intervalo de confiança para \(\mu_1\) – \(\mu_2\) , sendo \((1-\alpha)\) o nível de confiança, é dado por:
\[\begin{align} (\bar{X_1}- \bar{X_2}) - z_{1-\alpha/2}\ \sigma \leq (\mu_1 - \mu_2) \leq (\bar{X_1}- \bar{X_2}) + z_{1-\alpha/2}\ \sigma \tag{16.2} \end{align}\]
onde
\(\begin{aligned} &\ \sigma = \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} \end{aligned}\)
Como, em geral, as variâncias não são conhecidas, então elas devem ser estimadas por meio das variâncias amostrais. Sob determinadas condições, uma análise frequentemente utilizada quando não se conhece as variâncias nas duas populações se baseia na distribuição t de Student.
16.2.1 Teste t de Student para amostras independentes
Quando as variáveis possuem distribuições normais com a mesma variância, \(X_1 \sim N(\mu_1, \sigma^2)\) e \(X_2 \sim N(\mu_2, \sigma^2)\), mas a variância não é conhecida, um estimador da variância comum pode ser obtido a partir da média ponderada dos estimadores das variâncias nas amostras 1 (\(S_1^2\)) e 2 (\(S_2^2\)), com pesos respectivamente iguais a \(n_1 - 1\) e \(n_2 - 1\):
\(\begin{aligned} &\ S^2 = \frac{(n_1 - 1)S_1^2+(n_2 - 1)S_2^2}{n_1+n_2-2} \end{aligned}\)
onde:
\(\begin{aligned} &\ S_1^2 = \frac{1}{n_1 - 1} \sum_{i=1}^{n_1}(X_{1i}-\bar{X_1})^2 \end{aligned}\)
e
\(\begin{aligned} &\ S_2^2 = \frac{1}{n_2 - 1} \sum_{i=1}^{n_2}(X_{2i}-\bar{X_2})^2 \end{aligned}\)
A estatística
\[\begin{align} &\ T = \frac{(\bar{X_1}- \bar{X_2}) - (\mu_1-\mu_2)}{S \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \tag{16.3} \end{align}\]
possui uma distribuição t de Student com \(n_1 + n_2 - 2\) graus de liberdade (gl). A estatística:
\(\begin{aligned} &\ T = \frac{(\bar{X_1}- \bar{X_2})}{S \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \end{aligned}\)
pode ser utilizada para realizar um teste de hipótese bilateral para \(H_0: \mu_1 - \mu_2 = 0\) ou testes unilaterais para \(H_0: \mu_1 - \mu_2 \ge 0\) ou \(H_0: \mu_1 - \mu_2 \le 0\).
O intervalo com nível de confiança \((1-\alpha)\) para a diferença de médias entre os dois grupos é dado por:
\[\begin{align} (\bar{X_1}-\bar{X_2})-t_{gl,1-\alpha/2}{S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\leq(\mu_1-\mu_2)\leq(\bar{X_1}-\bar{X_2})+t_{gl,1-\alpha/2}{S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \tag{16.4} \end{align}\]
Vamos utilizar o R Commander para realizar um teste de hipótese bilateral de igualdade de médias e calcular o intervalo de confiança ao nível de 90% para o conjunto de dados energy. Tendo selecionado o conjunto de dados energy, utilizamos a seguinte opção do menu do R Commander para realizar um teste t paras amostras independentes:
\[\text{Estatísticas} \Rightarrow \text{Médias} \Rightarrow \text{Teste t para amostras independentes...}\]
Após a seleção do teste, é preciso definir a variável que define os grupos e a variável resposta (figura 16.4).
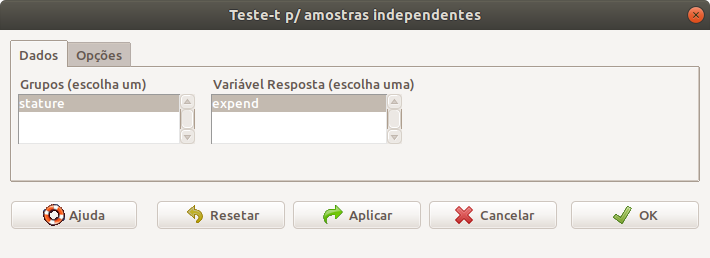
Figura 16.4: Seleção das variáveis de resposta e da variável que define os grupos. O conjunto de dados energy somente tem uma variável como fator e uma variável quantitativa como resposta.
Ao clicarmos na guia Opções na caixa de diálogo da figura 16.4, podemos selecionar o tipo de teste (bilateral/unilateral), o nível de confiança e se as variâncias são iguais ou não (figura 16.5). Vamos especificar o nível de confiança igual a 90% (0.9) e marcar a opção que as variâncias são iguais.
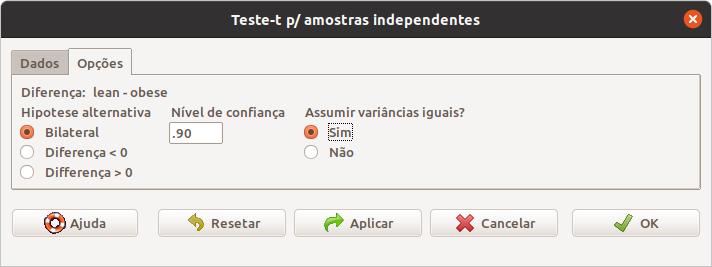
Figura 16.5: Definindo o tipo de teste, o nível de confiança e especificando que as variâncias são iguais.
Ao clicarmos em OK na figura 16.5, o teste t é realizado e os resultados são mostrados a seguir.
##
## Two Sample t-test
##
## data: expend by stature
## t = -3.9456, df = 20, p-value = 0.000799
## alternative hypothesis: true difference in means between group lean and group obese is not equal to 0
## 90 percent confidence interval:
## -3.207130 -1.256118
## sample estimates:
## mean in group lean mean in group obese
## 8.066154 10.297778Observem a sintaxe do comando que é executado para a realização do teste.
A saída mostra que o valor de p é 0,0008. Nesse caso, a hipótese nula deve ser rejeitada. O intervalo de confiança ao nível de 90% para a diferença de médias do consumo de energia entre as populações de mulheres magras e obesas varia de -3,2 a -1,26 MJ. Observem que o intervalo de confiança não inclui o zero (hipótese nula).
Se as variáveis X1 e X2 possuem distribuição normal, mas com variâncias desconhecidas e diferentes, um procedimento confiável é conhecido como teste t para duas amostras de Welch. Por essa aproximação, a variável aleatória
\[\begin{align} T = \frac{(\bar{X_1}- \bar{X_2}) - (\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}} \tag{16.5} \end{align}\]
segue uma distribuição t de Student com graus de liberdade dado pela seguinte expressão:
\[\begin{align} gl = \frac{(\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2})^2} {\frac{(\frac{S_1^2}{n_1})^2}{n_1-1} + \frac{(\frac{S_2^2}{n_2})^2}{n_2-1}} \tag{16.6} \end{align}\]
A estatística
\(\begin{aligned} &\ T = \frac{(\bar{X_1}- \bar{X_2})}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}} \end{aligned}\)
pode ser utilizada para realizar um teste de hipótese bilateral para \(H_0: \mu_1 - \mu_2 = 0\) ou testes unilaterais para \(H_0: \mu_1 - \mu_2 \ge 0\) ou \(H_0: \mu_1 - \mu_2 \le 0\).
O intervalo com nível de confiança \((1-\alpha)\) para a diferença de médias entre as duas amostras é dado por:
\[\begin{align} &(\bar{X_1}-\bar{X_2})-t_{gl,1-\alpha/2}\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}\leq(\mu_1-\mu_2)\leq(\bar{X_1}-\bar{X_2})+t_{gl,1-\alpha/2}\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}} \tag{16.7} \end{align}\]
Para realizarmos um teste de hipótese bilateral e calcularmos o intervalo de confiança ao nível de 90% para o conjunto de dados energy, supondo que as variâncias sejam diferentes, seguimos os mesmos passos das figuras 16.4 e 16.5, porém, não assumimos que as variâncias são iguais na aba Opções (figura 16.6).
Figura 16.6: Definindo o tipo de teste, o nível de confiança e especificando que as variâncias são diferentes
Ao clicarmos em OK na figura 16.6, o teste t para duas amostras de Welch é realizado e a saída é mostrada a seguir.
##
## Welch Two Sample t-test
##
## data: expend by stature
## t = -3.8555, df = 15.919, p-value = 0.001411
## alternative hypothesis: true difference in means between group lean and group obese is not equal to 0
## 90 percent confidence interval:
## -3.242484 -1.220763
## sample estimates:
## mean in group lean mean in group obese
## 8.066154 10.297778Os resultados nesse exemplo são bastante semelhantes aos obtidos com a suposição de que as variâncias são iguais.
Quando as duas amostras possuem o mesmo número de elementos (\(n_1 = n_2 = n\)), o número de graus de liberdade, calculado pela expressão (16.6), é igual \(2n-2\), as estatísticas (16.3) e (16.5) são iguais, assim como os intervalos de confiança (16.7) e (16.4). Isso significa que quando as amostras possuem o mesmo tamanho, o teste t de Student é idêntico ao teste t de Welch.
Uma condição necessária para se realizar um teste t de Student ou o teste t aproximado de Welch é que as variáveis \(X_1\) e \(X_2\) sejam normalmente distribuídas. O teste t é robusto para desvios consideráveis da hipótese de normalidade dos dados, especialmente se os tamanhos das amostras são iguais ou aproximados e especialmente quando os testes são bilaterais.
Mesmo quando as variáveis possuem grandes desvios em relação à distribuição normal, como a distribuição da média amostral tende a uma distribuição normal à medida que o tamanho da amostra aumenta (Teorema do Limite Central), se as amostras são suficientemente grandes (digamos \(n_1, n_2 \ge 30\)), podemos usar a estatística (16.1) para realizarmos um teste de hipótese bilateral para \(H_0: \mu_1 - \mu_2 = 0\) ou testes unilaterais para \(H_0: \mu_1 - \mu_2 \ge 0\) ou \(H_0: \mu_1 - \mu_2 \le 0\), e a expressão (16.2) para o cálculo do intervalo de confiança para a diferença de médias, com \(\sigma_1^2\) e \(\sigma_2^2\) substituídos por suas estimativas amostrais \(S_1^2\) e \(S_2^2\).
Para amostras pequenas, digamos \(n_1\ ou\ n_2 < 30\), é necessário verificar a normalidade das variáveis \(X_1\) e \(X_2\) e a igualdade de suas variâncias.
16.2.2 Teste de igualdade de variâncias
O conteúdo desta seção pode ser visualizado neste vídeo.
Na seção 16.2.1 foram realizados dois testes t para a comparação de médias entre dois grupos independentes cujas variáveis seguem uma distribuição normal: um supondo que as variâncias dos grupos fossem iguais e outro na suposição de que as variâncias fossem diferentes. Há vários testes estatísticos para verificar a suposição de que as variâncias de duas populações sejam iguais. Para realizar tais testes, como sempre, temos que definir a hipótese nula H0 e a hipótese alternativa H1, bem como qual a estatística a ser utilizada no teste. Para a variância, sendo \(S_1^2\) e \(S_2^2\) as estimativas amostrais das variâncias \(\sigma_1^2\) e \(\sigma_2^2\), respectivamente, de duas variáveis com distribuição normal, teríamos:
H0: \(\sigma_1^2 =\sigma_2^2\)
H1: \(\sigma_1^2 \neq \sigma_2^2\)
Estatística de teste: um dos testes para verificação de igualdade de variâncias é o teste F para duas variâncias. Nesse caso, utiliza-se uma das duas estatísticas a seguir:
\[\begin{align} F_1 = \frac{S_1^2}{S_2^2} \tag{16.8} \end{align}\]
ou
\[\begin{align} F_2 = \frac{S_2^2}{S_1^2} \tag{16.9} \end{align}\]
A estatística (16.8) segue uma distribuição chamada F de Fisher, com (n1 – 1) e (n2 – 1) graus de liberdade, que é a razão entre duas distribuições qui-quadrado, a primeira com (n1 – 1) graus de liberdade e a segunda com (n2 – 1) graus de liberdade:
\(\begin{aligned} &\ F_1 \sim \frac{\chi_{\nu_1}^2/\nu_1}{\chi_{\nu_2}^2/\nu_2} \end{aligned}\)
A estatística (16.9) segue uma distribuição F de Fisher, com (n2 – 1) e (n1 – 1) graus de liberdade, que é a razão entre duas distribuições qui-quadrado, a primeira com (n2 – 1) graus de liberdade e a segunda com (n1 – 1) graus de liberdade:
\(\begin{aligned} &\ F_2 \sim \frac{\chi_{\nu_2}^2/\nu_2}{\chi_{\nu_1}^2/\nu_1} \end{aligned}\)
A estatística utilizada no teste F é o maior valor entre \(F_1\) e \(F_2\). Sob a hipótese nula de igualdade de variâncias, espera-se que o maior valor entre \(F_1\) e \(F_2\) esteja próximo de 1. Se essa razão for maior ou igual ao valor crítico, então a hipótese de igualdade de variâncias é rejeitada.
No exemplo do conjunto de dados energy, os graus de liberdade \(\nu_1\) e \(\nu_2\) são dados por 12 e 8, respectivamente. Para realizarmos esse teste no R Commander, selecionamos a seguinte opção:
\[\text{Estatísticas} \Rightarrow \text{Variâncias} \Rightarrow \text{Teste F para 2 variâncias}\]
Na caixa de diálogo do teste F para 2 variâncias (figura 16.7), selecionamos a variável que define os grupos e a variável resposta. Em Opções, selecionamos o tipo de teste (bilateral/unilateral) e o nível de confiança.
Figura 16.7: Seleção das variáveis de resposta e da variável que define os grupos. O conjunto de dados energy somente tem uma variável como fator e uma variável quantitativa como resposta.
Ao clicarmos no botão OK, o teste é realizado de acordo com a função abaixo.
##
## F test to compare two variances
##
## data: expend by stature
## F = 0.78445, num df = 12, denom df = 8, p-value = 0.6797
## alternative hypothesis: true ratio of variances is not equal to 1
## 90 percent confidence interval:
## 0.2388735 2.2345455
## sample estimates:
## ratio of variances
## 0.784446Com base nos resultados, vemos que o valor para a maior das estatísticas (16.8) e (16.9) está dentro do intervalo de não rejeição da hipótese de que as variâncias sejam iguais. Portanto não há evidência suficiente para rejeitarmos a hipótese nula de que as variâncias sejam iguais. Porém o intervalo de confiança para a razão entre as variâncias \([0,24 - 2,2]\) é bastante amplo, de modo que esse teste possui pouco poder estatístico, ou seja, pouca capacidade de rejeitar a hipótese de igualdade de variâncias, se elas forem diferentes.
Há diversos outros testes para verificar a igualdade de 2 variâncias. No R Commander, dois outros podem ser executados (teste de Bartlett e teste de Levene) via mesma opção do menu que leva ao teste F para 2 variâncias. Em geral esses testes não possuem grande poder estatístico, especialmente quando as distribuições das variáveis \(X_1\ e\ X_2\) não são normais. Então, se houver dúvidas de que as variâncias são iguais, o mais indicado é realizar o teste t para duas amostras de Welch, na suposição de que as variâncias são diferentes.
16.2.3 Normalidade dos dados
O conteúdo desta seção e da seção 16.2.4 podem ser visualizados neste vídeo.
O teste t para diferença de duas médias para grupos independentes supõe que os dados sejam normalmente distribuídos. Um instrumento visual útil para checar a normalidade de dados é o gráfico de probabilidade normal (normal probability plot ou qqplot). No R Commander, esse gráfico é obtido por meio da opção Gráfico de comparação de quantis….
O gráfico de probabilidade normal é construído a partir da ordenação dos valores da variável em ordem crescente e a plotagem em um gráfico do i-ésimo valor contra o quantil esperado desse valor em uma distribuição normal. Ao plotar todos os pontos assim obtidos, obteríamos uma linha reta se os dados seguissem uma distribuição normal. Diferentes fontes usam diferentes aproximações para o cálculo do quantil esperado do i-ésimo valor.
A fórmula usada pelo R é dada por:
\[\begin{align} z_i = \Phi^{-1} \left(\frac{i-a}{n+1-2a}\right) \tag{16.10} \end{align}\]
para i = 1, 2, …, n, onde:
\(\begin{aligned} a = \begin{cases} 3/8,\ n \leq 10 \\ 0,5,\ n > 10 \end{cases} \end{aligned}\)
e \(\Phi^{-1}\) é a função quantil da distribuição normal.
Vamos mostrar como seriam obtidos os pares de pontos para construir o qqplot para o grupo de obesas do conjunto de dados energy. Primeiramente iremos selecionar todas os valores do consumo energético para o grupo de mulheres obesas, usando o comando abaixo.
Nesse comando, criamos uma variável (obesas_exp) que irá conter os valores do consumo energético das mulheres obesas. A expressão entre colchetes (stature == ‘obese’) testa cada valor de stature e será verdadeira somente para as observações de mulheres obesas. Então a expressão expend[stature == ‘obese’ retorna todos os valores de expend das mulheres obesas.
Vamos ordenar a variável obesas_exp em ordem crescente:
## [1] 8.79 9.19 9.21 9.68 9.69 9.97 11.51 11.85 12.79Temos nove valores na variável obesas_exp. Substituindo a = 3/8 = 0,375 e n = 9 na expressão (16.10), temos:
\(\begin{aligned} &\ z_i = \Phi^{-1} \left(\frac{i-0,375}{9,25}\right) \end{aligned}\)
A tabela 16.1 mostra os valores de zi correspondentes a cada valor de expend para o grupo de mulheres obesas.
| obesas_exp | i | (i-0,375)/9,25 | zi |
|---|---|---|---|
| 8,79 | 1 | 0,0675 | -1,49 |
| 9,19 | 2 | 0,176 | -0,93 |
| 9,21 | 3 | 0,284 | -0,57 |
| 9,68 | 4 | 0,392 | -0,27 |
| 9,69 | 5 | 0,500 | 0,00 |
| 9,97 | 6 | 0,608 | 0,27 |
| 11,51 | 7 | 0,716 | 0,57 |
| 11,85 | 8 | 0,824 | 0,93 |
| 12,79 | 9 | 0,932 | 1,49 |
Para gerar o gráfico de comparação de quantis no R Commander, usamos a seguinte opção:
\[\text{Gráficos} \Rightarrow \text{Gráfico de comparação de quantis...}\]
Na figura 16.8, selecionamos a variável desejada (expend). Em seguida, clicamos em Gráfico por grupos e selecionamos a variável stature (figura 16.9). Clicamos em OK e, a seguir, clicamos na aba Opções para verificar as opções disponíveis (figura 16.10). Vamos selecionar a distribuição normal e a opção não identificar em Identificar pontos.
Figura 16.8: Diálogo do gráfico de comparação de quantis para selecionar a variável cujo gráfico será construído.
Figura 16.9: Diálogo para a seleção da variável de agrupamento para o gráfico de comparação de quantis.
Figura 16.10: Caixa de diálogo de opções do gráfico de comparação de quantis.
Ao pressionarmos o botão OK, o comando a seguir é executado e o gráfico é mostrado na figura 16.11. Observando os dois gráficos, verificamos que há três pontos no grupo das mulheres magras que se desviam do que seria esperado em uma distribuição normal.
with(energy, qqPlot(expend, dist="norm", id=list(method="y", n=0,
labels=rownames(energy)), groups=stature))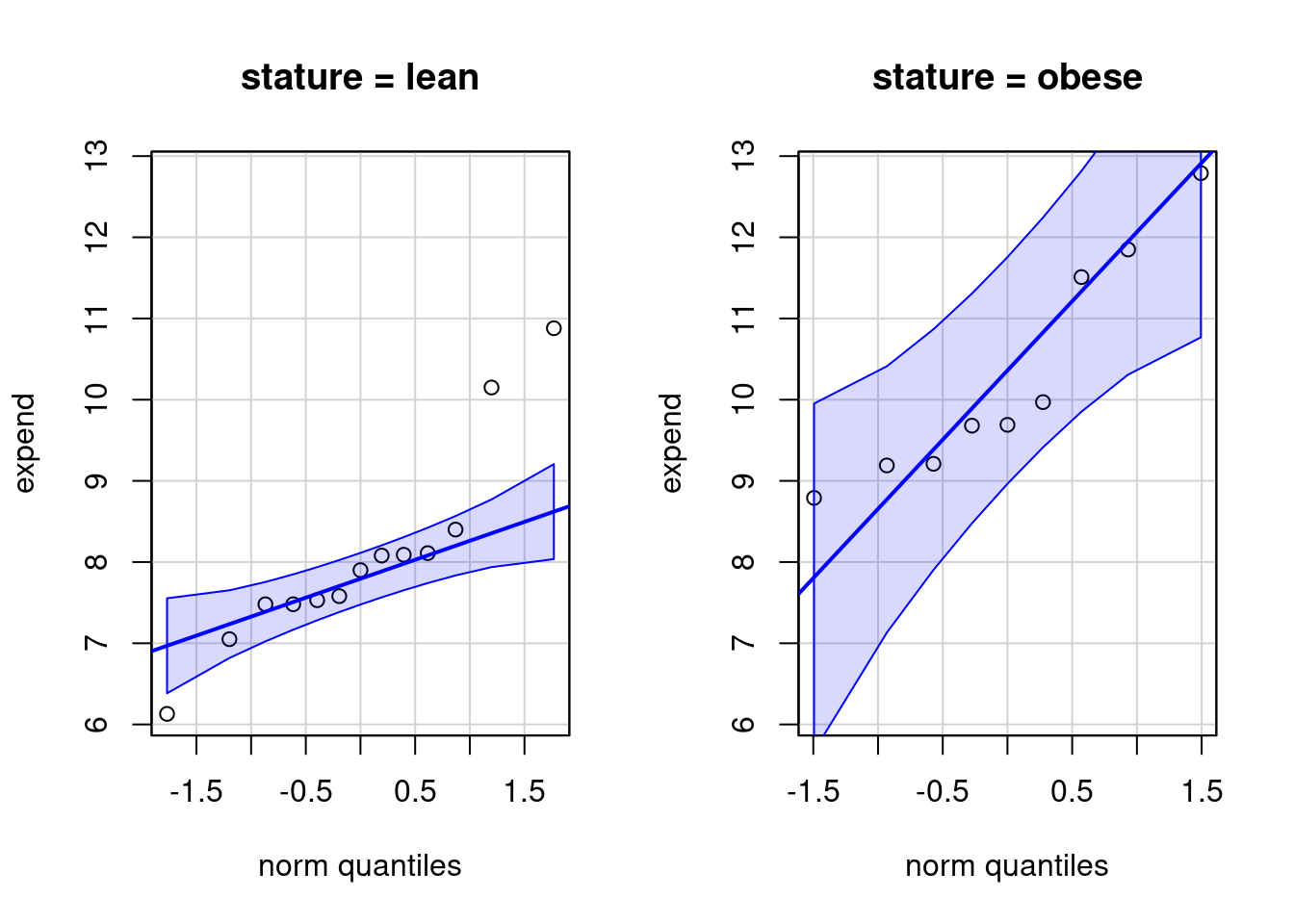
Figura 16.11: Gráfico de comparação de quantis da variável expend para os dois grupos de mulheres (obesas e magras).
16.2.4 Testes de normalidade
Além do gráfico de comparação de quantis, há vários testes estatísticos para verificar a hipótese de normalidade de dados.
Dois testes frequentemente utilizados são Kolmogorov-Smirnov e Shapiro-Wilk. Detalhes desses testes podem ser vistos nos links indicados. O teste de Shapiro-Wilk tende a ser mais poderoso para um mesmo nível de significância do que o teste de Kolmogorov-Smirnov, mas ambos podem detectar desvios insignificantes da normalidade quando a amostra for grande.
Para realizar um teste de normalidade no R Commander, usamos a seguinte opção:
\[\text{Estatísticas} \Rightarrow \text{Resumos} \Rightarrow \text{Test of normality...}\]
Na figura 16.12, selecionamos a variável desejada (expend). Em seguida, clicamos no botão Test by groups e selecionamos a variável stature como variável de agrupamento, porque precisamos testar a normalidade da variável expend em cada um dos grupos. Vamos realizar o teste de Shapiro-Wilk.
Figura 16.12: Caixa de diálogo para selecionar a variável cuja normalidade será testada, o teste a ser realizado e, eventualmente a variável de agrupamento.
Ao pressionarmos o botão OK, o comando a seguir é executado.
##
## --------
## stature = lean
##
## Shapiro-Wilk normality test
##
## data: expend
## W = 0.86733, p-value = 0.04818
##
## --------
## stature = obese
##
## Shapiro-Wilk normality test
##
## data: expend
## W = 0.87603, p-value = 0.1426
##
## --------
##
## p-values adjusted by the Holm method:
## unadjusted adjusted
## lean 0.048184 0.096367
## obese 0.142574 0.142574Os resultados mostram o valor de p resultante da aplicação do teste de normalidade de Shapiro-Wilk para a variável expend em cada um dos grupos da variável stature (p = 0,048 para as magras e p = 0,14 para as obesas). Como são realizados dois testes, há uma correção dos valores de p para múltiplos testes, usando o método de Holm, resultando em valores de p = 0,096 para as magras e p = 0,14 para as obesas. Continuando com o nível de significância de 10% que estamos usando neste capítulo, mesmo com a correção de Holm, rejeitaríamos a hipótese de normalidade dos valores da variável energy para as mulheres magras (p = 0,096 < 0,1). Esses resultados estão de acordo com os obtidos no gráfico de comparação de quantis, indicando um ligeiro desvio da normalidade para as mulheres magras.
16.2.5 Teste não paramétrico de Wilcoxon para duas amostras
O conteúdo desta seção pode ser visualizado neste vídeo.
Para a comparação de médias entre duas amostras independentes, quando as distribuições das variáveis \(X_1\ e\ X_2\) se desviam marcadamente da normal e as amostras são pequenas (\(n_1\ ou\ n_2 < 30\)), então pode-se utilizar o teste não paramétrico denominado teste de Mann-Whitney, que é equivalente ao teste de Wilcoxon para duas amostras.
O teste de Wilcoxon para duas amostras também é conhecido como teste de Wilcoxon-Mann-Whitney ou teste de Wilcoxon da soma dos postos (Wilcoxon rank-sum test). Esse teste relaxa a exigência de normalidade dos dados, porém requer que as seguintes condições sejam verdadeiras:
as duas amostras foram aleatoriamente e independentemente extraídas das suas respectivas populações;
a escala da medição é pelo menos ordinal;
se as distribuições das populações diferem, elas diferem somente em relação à sua localização.
Vamos retornar ao conjunto de dados energy, apresentado na seção 16.2. Nessa seção, foi realizado um teste t para amostras independentes. Vamos utilizar esse conjunto de dados para ilustrar o teste de Mann-Whitney.
Os valores da variável dependente (expend) são ordenados em ordem crescente (ou decrescente), independentemente do grupo ao qual pertencem. A tabela 16.2 mostra os valores ordenados em ordem crescente nas colunas 1 (grupo “magras”) e 2 (grupo “obesas”). Após a ordenação, cada valor é substituído pela sua ordem (posto) na sequência de valores. Por exemplo, o menor valor recebe o posto 1, o segundo menor valor recebe o posto 2 e assim por diante. Quando houver mais de um valor iguais entre si (empates), cada um deles recebe a média dos postos que receberiam se fossem diferentes. Por exemplo, há dois valores iguais a 7,48 nas posições 3 e 4. Portanto eles recebem o posto igual a 3,5. Os postos para a variável expend em cada grupo são mostrados nas colunas 3 e 4 para os grupos “magras” e “obesas”, respectivamente.
| Consumo de energia Grupo ‘magras’ | Consumo de energia Grupo ‘obesas’ | Posto Grupo ‘magras’ | Posto Grupo ‘obesas’ |
|---|---|---|---|
| 6.13 | 1 | ||
| 7.05 | 2 | ||
| 7.48 | 3,5 | ||
| 7.48 | 3,5 | ||
| 7.53 | 5 | ||
| 7.58 | 6 | ||
| 7.9 | 7 | ||
| 8.08 | 8 | ||
| 8.09 | 9 | ||
| 8.11 | 10 | ||
| 8.4 | 11 | ||
| 8.79 | 12 | ||
| 9.19 | 13 | ||
| 9.21 | 14 | ||
| 9.68 | 15 | ||
| 9.69 | 16 | ||
| 9.97 | 17 | ||
| 10.15 | 18 | ||
| 10.88 | 19 | ||
| 11.51 | 20 | ||
| 11.85 | 21 | ||
| 12.79 | 22 | ||
| 103 | 150 |
Sejam n1 e n2 o número de valores nos grupos 1 e 2, R1 a soma dos postos no grupo 1, R2 a soma dos postos no grupo 2. As estatísticas a seguir são utilizadas pelo teste de Mann-Whitney:
\[\begin{align} U = n_1 n_2 + \frac{n_1(n_1 + 1)}{2} - R_1 \tag{16.11} \end{align}\]
\[\begin{align} U' = n_1 n_2 + \frac{n_2(n_2 + 1)}{2} - R_2 \tag{16.12} \end{align}\]
U pode ser obtido a partir de U’ e vice-versa. Na hipótese nula de igualdade de localização das duas distribuições, por exemplo, se uma das duas estatísticas (U ou U’) for maior ou igual ao valor crítico, rejeita-se a hipótese nula. No teste de Wilcoxon para duas amostras, definem-se estatísticas alternativas e equivalentes, que são dadas por:
\[\begin{align} W = R_1 - \frac{n_1(n_1 + 1)}{2} \tag{16.13} \end{align}\]
\[\begin{align} W' = R_2 - \frac{n_2(n_2 + 1)}{2} \tag{16.14} \end{align}\]
Vamos realizar o teste de Wilcoxon para duas amostras no R Commander para comparar a variável expend nos grupos de mulheres “magras” e “obesas”. Vamos realizar um teste de hipótese bilateral. Tendo selecionado o conjunto de dados energy, utilizamos a seguinte opção do menu do R Commander:
\[\text{Estatísticas} \Rightarrow \text{Testes Não-Paramétricos} \Rightarrow \text{Teste de Wilcoxon (2 amostras)}\]
Após a seleção do teste, é preciso definir a variável que define os grupos e a variável resposta (figura 16.13).
Figura 16.13: Seleção das variáveis de resposta e da variável que define os grupos.
Ao clicarmos na guia Opções na caixa de diálogo da figura 16.13, podemos selecionar se o teste é bilateral ou unilateral e o tipo de teste (figura 16.14). Vamos selecionar a opção Exato para tipo de teste.
Figura 16.14: Definindo as opções para o teste de Wilcoxon para duas amostras. Observem que não é possível especificar o nível de confiança nessa caixa de diálogo.
Ao clicarmos em OK na figura 16.14, o teste de Wilcoxon para duas amostras é realizado conforme a seguir.
## lean obese
## 7.90 9.69##
## Wilcoxon rank sum test
##
## data: expend by stature
## W = 12, p-value = 0.001896
## alternative hypothesis: true location shift is not equal to 0Os resultados mostram as medianas dos grupos das mulheres “magras” e “obesas”, e o resultado do teste estatístico, com valor de p = 0,001896, rejeitando a hipótese nula de igualdade de localização (medianas) das distribuições dos dois grupos de mulheres.
Para calcular o intervalo de confiança para a diferença de localização entre as duas populações, é necessário utilizar a linha de comando. A função wilcox.test com a especificação do nível de confiança (conf.level = 0.90) e determinando que o intervalo de confiança seja calculado (conf.int = TRUE) é mostrada a seguir seguida dos resultados.
wilcox.test(expend ~ stature, alternative='two.sided', exact=TRUE,
correct=FALSE, data=energy, conf.int=TRUE, conf.level=0.90)##
## Wilcoxon rank sum test
##
## data: expend by stature
## W = 12, p-value = 0.001896
## alternative hypothesis: true location shift is not equal to 0
## 90 percent confidence interval:
## -3.419949 -1.310093
## sample estimates:
## difference in location
## -1.909972Há diversos detalhes sobre o teste de Wilcoxon para duas amostras realizado pelo R que são apresentados na página de ajuda da função wilcox.test (acessada por meio do comando ?wilcox.test). Devemos chamar a atenção que a diferença de localização mostrada nos resultados acima não estima a diferença de medianas dos grupos, mas sim a mediana da diferença entre um item de \(X_1\) e um item de \(X_2\).
No exemplo acima, podemos dizer, com confiança de 90%, que a mediana do consumo de energia de uma mulher magra é pelo menos 1,31 menor do que a mediana de uma mulher obesa.
16.3 Comparação de médias de amostras dependentes
O conteúdo desta seção e da seção 16.3.1 podem ser visualizados neste vídeo.
Para amostras dependentes (pareadas), vamos usar como exemplo o conjunto de dados intake da biblioteca ISwR.
## pre post
## 1 5260 3910
## 2 5470 4220
## 3 5640 3885
## 4 6180 5160
## 5 6390 5645
## 6 6515 4680
## 7 6805 5265
## 8 7515 5975
## 9 7515 6790
## 10 8230 6900
## 11 8770 7335O conjunto de dados intake contém dados de consumo de energia (kJ) em 11 pacientes antes e depois da menstruação.
Como os dados são pareados, a melhor forma de analisá-los estatisticamente para verificar se existe uma diferença de médias entre as medidas antes (\(X_1\)) e depois (\(X_2\)) é criar uma variável aleatória consistindo da diferença entre as medidas antes e depois:
\[D = X_1 - X_2\]
Vamos considerar diferentes situações.
Se a variável D possui uma distribuição \(N(\mu_D, \sigma_D^2)\) com variância conhecida, a estatística
\[\begin{align} Z = \frac{\bar{D} - \mu_D}{\sqrt{\frac{\sigma_D^2}{n}}} \end{align}\]
possui uma distribuição normal padrão. A estatística
\[\begin{align} Z = \frac{\bar{D}}{\sqrt{\frac{\sigma_D^2}{n}}} \tag{16.15} \end{align}\]
onde n é o tamanho da amostra, pode ser utilizada para realizar um teste de hipótese bilateral para \(H_0: \mu_D = 0\) ou testes unilaterais para \(H_0: \mu_D \ge 0\) ou \(H_0: \mu_D \le 0\).
O intervalo de confiança para \(\mu_D\) (diferença de médias entre as duas medidas), sendo \((1-\alpha)\) o nível de confiança, é dado por:
\[\begin{align} \bar{D} - z_{1-\alpha/2} \sqrt{\frac{\sigma_D^2}{n}} \leq \mu_D \leq \bar{D} + z_{1-\alpha/2} \sqrt{\frac{\sigma_D^2}{n}} \tag{16.16} \end{align}\]
Como, em geral, a variância de D não é conhecida, ela deve ser estimada por meio da variância amostral. Sob a condição de normalidade, uma análise frequentemente utilizada quando não se conhece a variância da diferença das observações se baseia na distribuição t de Student.
16.3.1 Teste t para amostras dependentes (teste t pareado)
Se a variável D possui uma distribuição \(N(\mu_D, \sigma_D^2)\) com variância desconhecida, a variância da diferença entre as medidas pode ser estimada pela expressão:
\[\begin{align} S_D^2 = \frac{1}{n-1}\sum_{i=1}^{n}(D_i-\bar{D})^2 \tag{16.17} \end{align}\]
Nesse caso, a estatística
\[\begin{align} T = \frac{\bar{D} - \mu_D}{\sqrt{\frac{S_D^2}{n}}} \end{align}\]
possui uma distribuição t de Student com n-1 graus de liberdade. A estatística
\[\begin{align} t = \frac{\bar{D}}{\sqrt{\frac{S_D^2}{n}}} \tag{16.18} \end{align}\]
pode ser utilizada para realizar um teste de hipótese bilateral para \(H_0: \mu_D = 0\) ou testes unilaterais para \(H_0: \mu_D \ge 0\) ou \(H_0: \mu_D \le 0\).
O intervalo de confiança para \(\mu_D\) (diferença de médias entre as duas medidas), sendo \((1-\alpha)\) o nível de confiança, é dado por:
\[\begin{align} \bar{D} - t_{n-1, 1-\alpha/2} \sqrt{\frac{S_D^2}{n}} \leq \mu_D \leq \bar{D} + t_{n-1, 1-\alpha/2} \sqrt{\frac{S_D^2}{n}} \tag{16.19} \end{align}\]
Vamos utilizar o R Commander para realizar um teste de hipótese bilateral e calcular o intervalo de confiança ao nível de 90% para o conjunto de dados intake. Tendo selecionado o conjunto de dados intake, utilizamos a seguinte opção do menu do R Commander para realizar um teste t paras amostras dependentes:
\[\text{Estatísticas} \Rightarrow \text{Médias} \Rightarrow \text{Teste t (dados pareados)}\]
Após a seleção do teste, é preciso definir as variáveis que definem as duas medidas efetuadas em cada unidade de observação (figura 16.15).
Figura 16.15: Seleção das variáveis que definem as duas medidas efetuadas em cada unidade de observação.
Ao clicarmos na guia Opções na caixa de diálogo da figura 16.15, podemos selecionar o tipo de teste (bilateral/unilateral) e o nível de confiança. Vamos especificar o nível de confiança igual a 90% (0.9) (figura 16.16). O teste verificará a diferença (post – pre).
Figura 16.16: Definindo o tipo de teste e o nível de confiança.
Ao clicarmos em OK na figura 16.16, o teste t pareado é realizado por meio da função t.test abaixo, com os resultados mostrados a seguir.
##
## Paired t-test
##
## data: pre and post
## t = 11.941, df = 10, p-value = 0.0000003059
## alternative hypothesis: true mean difference is not equal to 0
## 90 percent confidence interval:
## 1120.036 1520.873
## sample estimates:
## mean difference
## 1320.455Os resultados mostram que o intervalo com confiança de 90% da diferença pre – post é dado por [1120,0; 1520,9] kJ. O valor de p é 3,1.10-7 (bastante significativo), rejeitando a hipótese nula de que o consumo de energia é o mesmo antes e depois da menstruação.
Uma condição necessária para se realizar o teste t pareado é que a diferença das variáveis, \(D = X_1 - X_2\), seja normalmente distribuída. O teste t é robusto para desvios consideráveis da hipótese de normalidade dos dados e especialmente quando os testes são bilaterais.
Mesmo quando diferença das variáveis possui grandes desvios em relação à distribuição normal, se a amostra for suficientemente grande (digamos \(n \ge 30\)), podemos usar a estatística (16.15) para realizarmos um teste de hipótese bilateral para \(H_0: \mu_D = 0\) ou testes unilaterais para \(H_0: \mu_D \ge 0\) ou \(H_0: \mu_D \le 0\), e a expressão (16.16) para o cálculo do intervalo de confiança para a diferença de médias, com \(\sigma_D^2\) substituída por sua estimativa amostral, \(S_D^2\).
Para amostras pequenas, digamos \(n < 30\), é necessário verificar a normalidade da variável D.
Vamos verificar por meio do diagrama de comparação de quantis a normalidade da diferença (pre – post). Como não temos essa variável no conjunto de dados, precisamos criá-la. Vamos mostrar como fazer isso utilizando o R Commander. Para criar uma nova variável a partir de outras variáveis existentes no conjunto de dados ativo, acessamos a seguinte opção no menu:
\[\text{Dados} \Rightarrow \text{Modificação variáveis no conj. de dados...} \Rightarrow \text{Computar nova variável...}\]
Na caixa de diálogo da figura 16.17, damos o nome para a variável que vai ser criada e especificamos a fórmula de cálculo dessa nova variável (pre – post).
Figura 16.17: Nessa caixa de diálogo, damos o nome para a variável que vai ser criada e especificamos a fórmula de cálculo dessa nova variável.
Ao clicarmos em OK, a variável será criada por meio do comando a seguir e é adicionada ao conjunto de dados, como mostra a nova listagem de intake.
## pre post diff
## 1 5260 3910 1350
## 2 5470 4220 1250
## 3 5640 3885 1755
## 4 6180 5160 1020
## 5 6390 5645 745
## 6 6515 4680 1835
## 7 6805 5265 1540
## 8 7515 5975 1540
## 9 7515 6790 725
## 10 8230 6900 1330
## 11 8770 7335 1435Agora podemos gerar o gráfico de comparação de quantis para a variável diff, como na seção anterior, ou usando diretamente a função qqPlot como a seguir. O gráfico é mostrado na figura 16.18, indicando que a variável diff não possui grandes desvios em relação a uma distribuição normal.
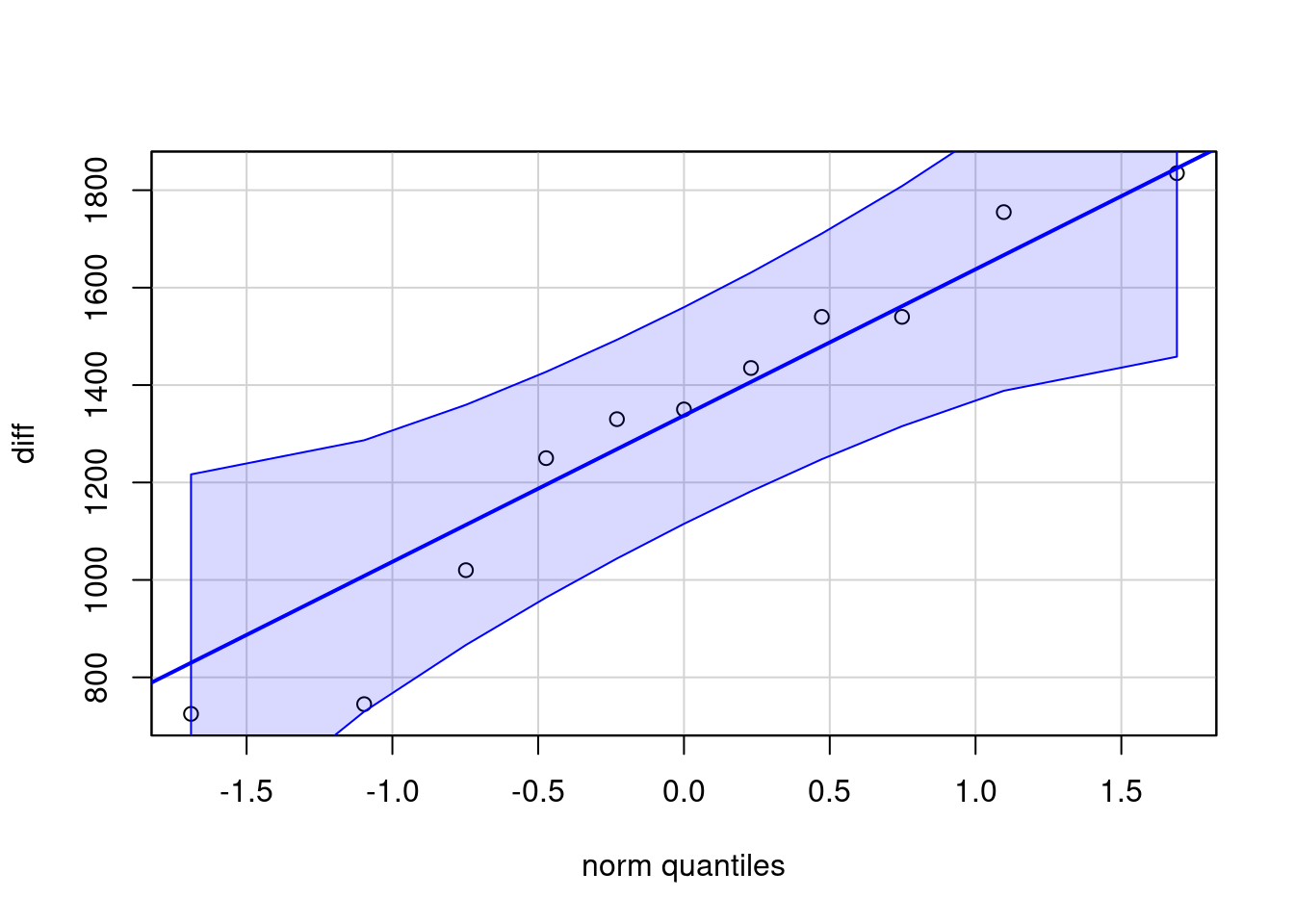
Figura 16.18: Gráfico de comparação de quantis da normal para a variável diff (pre – post).
Quando a a diferença de valores da variável resposta não possui uma distribuição normal e o tamanho da amostra é pequeno (n < 30), então pode-se utilizar o teste de Wilcoxon para amostras pareadas, apresentado na seção seguinte.
16.3.2 Teste de Wilcoxon para amostras pareadas
O conteúdo desta seção e da seção 16.5 podem ser visualizados neste vídeo.
Para duas amostras dependentes, o teste não paramétrico mais utilizado é denominado teste de Wilcoxon para amostras pareadas (Wilcoxon paired-sample test, Wilcoxon matched pairs test, signed-rank test). Esse teste consiste em colocar em ordem crescente ou decrescente as diferenças entre os valores da variável em cada par. O posto correspondente a cada diferença recebe o sinal positivo se a diferença for positiva e o sinal negativo e se a diferença for negativa. Em seguida são somados os postos positivos (ou negativos). A soma é então comparada com a distribuição da soma dos postos sob a hipótese nula.
Vamos retornar ao conjunto de dados intake, seção 16.3.1. A tabela 16.3 ordena os valores da diferença entre as variáveis pre e post na primeira coluna e soma os postos positivos na segunda coluna. Nesse exemplo, todos os postos são positivos, porque todas as diferenças são positivas.
| pre-post | Postos pre-post |
|---|---|
| 725 | 1 |
| 745 | 2 |
| 1020 | 3 |
| 1250 | 4 |
| 1330 | 5 |
| 1350 | 6 |
| 1435 | 7 |
| 1540 | 8,5 |
| 1540 | 8,5 |
| 1755 | 10 |
| 1835 | 11 |
| 66 |
Vamos realizar o teste de Wilcoxon para amostras pareadas no R Commander para comparar as variáveis pre e post do conjunto de dados intake. Vamos realizar um teste de hipótese bilateral e calcular o intervalo de confiança ao nível de 90%. Tendo selecionado o conjunto de dados intake, utilizamos a seguinte opção do menu do R Commander para realizar de Wilcoxon para amostras pareadas:
\[\text{Estatísticas} \Rightarrow \text{Testes Não-Paramétricos} \Rightarrow \text{Teste de Wilcoxon (amostras pareadas)}\]
Após a seleção do teste, é preciso definir as variáveis que correspondem à medida do consumo de energia antes e depois da menstruação (figura 16.19).
Figura 16.19: Seleção das variáveis que correspondem à medida do consumo de energia antes e depois da menstruação.
Ao clicarmos na guia Opções na caixa de diálogo da figura 16.19, podemos selecionar se o teste será bilateral ou unilateral e o tipo de teste (figura 16.20). Vamos selecionar a opção Exato.
Figura 16.20: Definindo as opções do teste de Wilcoxon para amostras pareadas. Observem que não é possível especificar o nível de confiança nessa caixa de diálogo.
Ao clicarmos em OK na figura 16.20, o teste de Wilcoxon para amostras pareadas é realizado como a seguir. Observem que o parâmetro paired = TRUE.
## [1] 1350##
## Wilcoxon signed rank test with continuity correction
##
## data: pre and post
## V = 66, p-value = 0.00384
## alternative hypothesis: true location shift is not equal to 0Os resultados mostram a mediana da diferença entre os valores de pre e post e o resultado do teste estatístico, com valor de p = 0,00384. Considerando o nível de significância igual a 10%, a hipótese nula de igualdade de localização das distribuições das variáveis pre e post é rejeitada.
Para calcularmos o intervalo de confiança para a diferença de localização entre as medidas das duas populações, é necessário utilizar a linha de comando. A função wilcox.test com as especificações do nível de confiança (conf.level = 0.90) e determinando que o intervalo de confiança seja calculado (conf.int = TRUE) é mostrada a seguir, e os resultados são apresentados logo após.
with(intake, wilcox.test(pre, post, alternative='two.sided', exact=TRUE,
paired=TRUE, conf.int=TRUE, conf.level=0.90))##
## Wilcoxon signed rank test with continuity correction
##
## data: pre and post
## V = 66, p-value = 0.00384
## alternative hypothesis: true location shift is not equal to 0
## 90 percent confidence interval:
## 1132.5 1540.0
## sample estimates:
## (pseudo)median
## 1341.332A pseudo mediana mostrada acima é o estimador de Hodges-Lehmann (Wikipedia 2019). Ele é um estimador não paramétrico e robusto de um parâmetro de localização da população. Para populações que são simétricas em relação à mediana, como a distribuição gaussiana ou t de Student, o estimador de Hodges-Lehmann é um estimador consistente e não enviesado da mediana da população. Para populações não simétricas, o estimador de Hodges-Lehmann é um estimador da pseudo mediana, que é proximamente relacionada à mediana da população.
16.4 Teste t pareado x Teste t não pareado
Vamos considerar o conjunto de dados sleep da biblioteca datasets (GPL-3). As funções abaixo carregam o pacote datasets, o conjunto de dados sleep e mostram as observações de 2 pacientes (2 linhas por paciente) do conjunto de dados sleep.
## extra group ID
## 1 0.7 1 1
## 2 -1.6 1 2
## 11 1.9 2 1
## 12 0.8 2 2O conjunto de dados sleep mostra o efeito de dois medicamentos soporíficos em 10 pacientes. A variável extra indica o aumento de horas de sono após o uso dos medicamentos. A variável group possui dois valores: 1 indica um dos medicamentos e 2 indica o outro medicamento. A variável ID indica o paciente. Assim a primeira linha mostra o número de horas extras de sono do paciente 1 após o uso do medicamento 1. A linha 11 mostra o número de horas extras de sono do paciente 1 após o uso do medicamento 2 e assim por diante.
Observem que são realizadas duas medidas em cada paciente, cada medida com um medicamento. Essas medidas tendem a ser correlacionadas. Vamos ver o que acontece se tratássemos esses dados como se fossem duas amostras de pacientes distintos e realizássemos um teste t para amostras independentes (não pareado). Utilizando a variável group para separar os dois grupos de pacientes e seguindo passos análogos aos da seção 16.2, executaríamos a função t.test conforme a seguir. Dessa vez, vamos definir o nível de confiança igual a 95%.
##
## Welch Two Sample t-test
##
## data: extra by group
## t = -1.8608, df = 17.776, p-value = 0.07939
## alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
## 95 percent confidence interval:
## -3.3654832 0.2054832
## sample estimates:
## mean in group 1 mean in group 2
## 0.75 2.33O intervalo de confiança para a diferença de médias entre os dois medicamentos inclui o valor 0, o valor de p é 0,079 e, portanto, a hipótese nula de igualdade de médias não é rejeitada ao nível de significância de 5%. Porém, como os pacientes são os mesmos nos dois grupos, o teste t para amostras independentes não é o mais indicado para essa situação.
A interface gráfica do R Commander não permite realizar um teste pareado com os dados de sleep, porque os dados não estão organizados conforme os dados da seção anterior (conjunto de dados intake), onde cada medida é representada por uma variável diferente. Precisamos usar a linha de comando para realizar o teste t pareado. A seguinte função realiza o teste t pareado para os dados de sleep.
##
## Paired t-test
##
## data: extra[group == 1] and extra[group == 2]
## t = -4.0621, df = 9, p-value = 0.002833
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
## -2.4598858 -0.7001142
## sample estimates:
## mean difference
## -1.58Agora o valor de p é 0,0028 (estatisticamente significativo) e o intervalo de confiança não inclui o zero. Para essa situação, o teste t pareado é mais poderoso do que o teste t não pareado, porque o desvio padrão da diferença de variáveis é calculado levando-se em conta somente a diferença dos valores em cada indivíduo. Assim o desvio padrão é bem menor do que o calculado no teste t para amostras independentes, que leva em conta a diferença entre indivíduos.
Vamos entender o comando. A função with possui dois parâmetros: um conjunto de dados (nesse exemplo sleep), e uma outra função (t.test), significando que a função t.test será aplicada sobre o conjunto de dados sleep. Nesse exemplo, três parâmetros são especificados para a função t.test. O primeiro parâmetro, extra[group == 1], seleciona as medidas (extra) do medicamento 1 (group == 1). A expressão entre colchetes funciona como um seletor dos valores da variável que precede os colchetes. O segundo parâmetro, extra[group == 2], seleciona as medidas (extra) do medicamento 2 (group == 2). Finalmente o terceiro parâmetro, paired = TRUE, informa que o teste t é pareado.
Vamos obter o diagrama de comparação de quantis para a diferença da variável extra para os dois medicamentos. Os seguintes comandos geram o diagrama (figura 16.21):
extra1 <- subset(sleep$extra, sleep$group == 1)
extra2 <- subset(sleep$extra, sleep$group == 2)
diff <- extra1 - extra2
qqPlot(diff, dist="norm", id=list(method="y", n=0))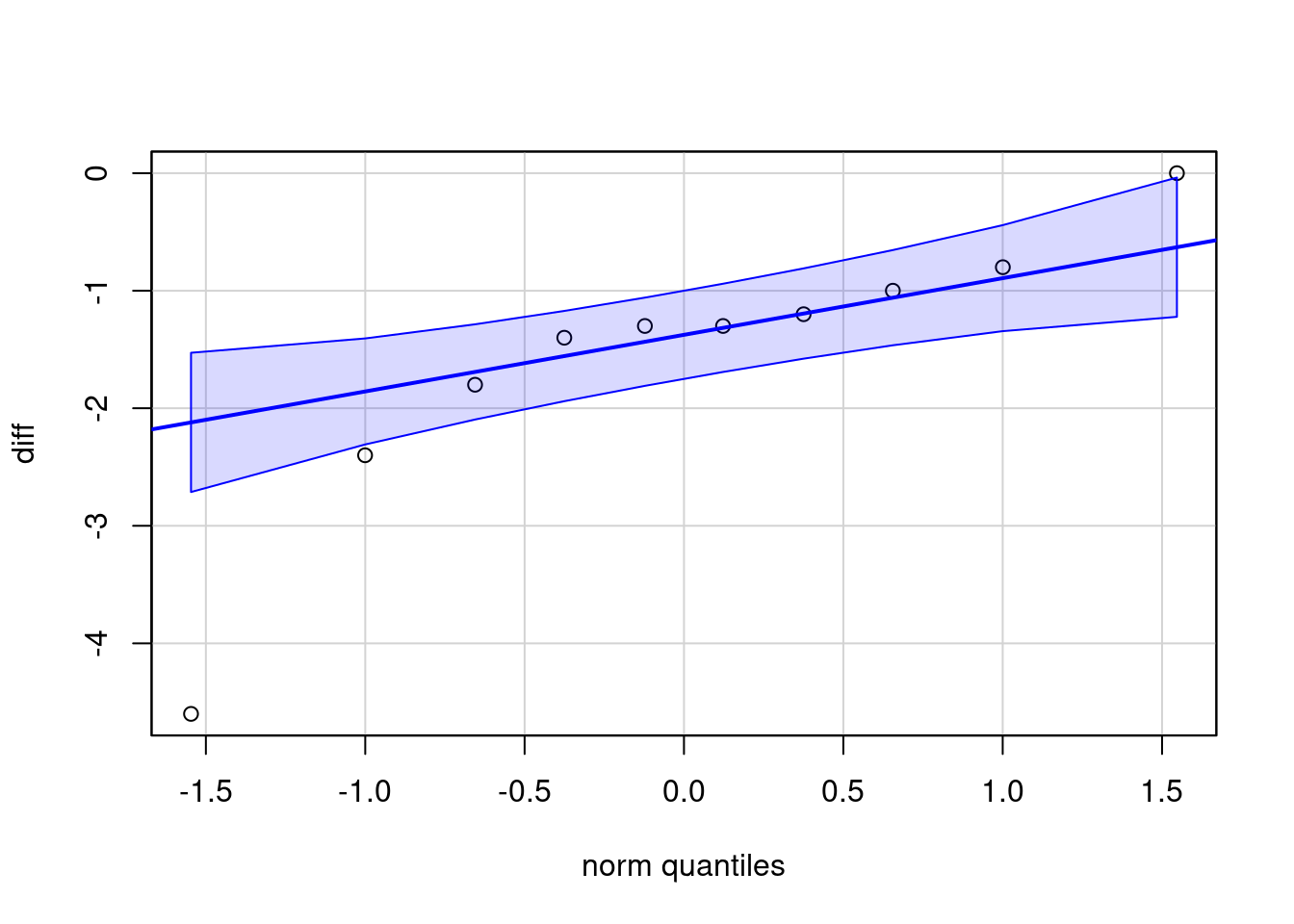
Figura 16.21: Gráfico de comparação de quantis da normal para a diferença dos valores da variável extra do conjunto de dados sleep para cada um dos medicamentos.
O primeiro comando cria a variável extra1 que contém os valores de extra para o medicamento 1. A função subset tem dois parâmetros: o primeiro informa a variável de onde o subconjunto será extraído (sleep$extra); o segundo parâmetro informa o critério de seleção (sleep$group == 1).
O segundo comando cria a variável extra2 que contém os valores de extra para o medicamento 2. O terceiro comando faz a subtração das duas variáveis extra1 e extra2, e a última função cria o diagrama. O diagrama indica que a variável diff não possui grandes desvios de uma distribuição normal, especialmente se considerarmos que a amostra é pequena.
Para o conjunto de dados sleep, não é possível fazer o teste de Wilcoxon para amostras pareadas, usando diretamente o menu do R Commander, já que os valores da variável extra não estão separados em duas variáveis, uma para cada medicamento. A função a seguir mostra como realizar o teste de Wilcoxon para amostras pareadas com os dados de sleep, especificando o nível de confiança de 0,95 e solicitando o cálculo do intervalo de confiança da pseudo mediana. Observem que os resultados levam às mesmas conclusões do teste t pareado.
with(sleep, wilcox.test(extra[group == 1], extra[group == 2],
alternative='two.sided', exact=TRUE, paired=TRUE,
conf.int = TRUE, conf.level = 0.95))##
## Wilcoxon signed rank test with continuity correction
##
## data: extra[group == 1] and extra[group == 2]
## V = 0, p-value = 0.009091
## alternative hypothesis: true location shift is not equal to 0
## 95 percent confidence interval:
## -2.949921 -1.050018
## sample estimates:
## (pseudo)median
## -1.40003116.5 Resumo das análises para comparar médias entre 2 grupos
Diante do exposto nas seções anteriores, podemos fazer um resumo dos principais testes utilizados para comparar medidas de localização entre dois grupos. Vamos separar em duas seções: amostras independentes e amostras dependentes.
16.5.1 Amostras Independentes
A tabela da figura 16.22 resume aproximadamente as análises que se aplicam a cada situação, quando se comparam medidas de localização entre dois grupos independentes.

Figura 16.22: Análises aplicáveis para a comparação de médias entre dois grupos independentes.
16.5.2 Amostras dependentes
A tabela da figura 16.23 resume aproximadamente as análises que se aplicam a cada situação, quando se comparam medidas de localização entre dois grupos dependentes.

Figura 16.23: Análises aplicáveis para a comparação de médias entre dois grupos dependentes.
16.6 Exercícios
Com o conjunto de dados birthwt, do pacote MASS (GPL-2 | GPL-3), faça as atividades abaixo.
- Verifique a ajuda para o conjunto de dados;
- Compare as médias da variável bwt (peso ao nascer) entre os grupos das mães que fumavam ou não durante a gestação.
- Obtenha o intervalo de confiança ao nível de 95% para a diferença das médias de peso ao nascer entre os dois grupos.
- Verifique as suposições para a realização do teste t para amostras independentes.
- Repita os itens “b” a “d” para a comparação das médias de peso ao nascer entre os grupos das mães com ou sem histórico de hipertensão.
O conjunto de dados WeightLoss do pacote carData (GPL-2 | GPL-3) contém dados artificiais sobre perda de peso e auto-estima ao longo de três meses, para três grupos de indivíduos: Controle, Dieta e Dieta + Exercício.
- Verifique a ajuda para o conjunto de dados.
- Crie um subconjunto de dados de WeightLoss, chamado wlDietEx, com dados somente dos indivíduos que fizeram dieta + exercício, por meio do comando ao final deste exercício.
- Com o conjunto de dados wlDietEx, compare as médias de perdas de peso no 2o e 3o mês. Utilize o nível de significância igual a 10%.
- Compare as médias de perdas de peso no 1o e 2o mês. Utilize o nível de significância igual a 10%.
- Verifique as suposições para a realização do teste t pareado nos itens “c” e “d”.