7 Probabilidade
7.1 Introdução
Os conteúdos desta seção e das seções 7.2 e 7.3 podem ser visualizados neste vídeo.
Em física, alguns modelos da mecânica clássica permitem prever como os fenômenos irão se comportar dentro de determinadas condições. Assim é possível prever com boa precisão a trajetória de satélites lançados no espaço, por exemplo. Esses modelos são chamados determinísticos.
Em saúde, em geral é difícil prever com precisão como as pessoas irão evoluir sob determinados tratamentos, ou quando expostas a determinadas condições. Os fatores que podem interferir em determinados eventos são frequentemente tão numerosos e, em muitos casos, até desconhecidos, que impedem a criação de modelos determinísticos. Entre a diversidade de fatores, podem-se citar a variação genética na população, diferentes condições socioeconômicas, variáveis comportamentais, etc. Por isso, mesmo sendo universalmente aceito que o fumo é um fator etiológico para o câncer do pulmão, nem todas as pessoas que fumam desenvolvem o câncer do pulmão. Assim sendo, em geral, há alguma incerteza associada aos fenômenos biológicos.
Há diversas formas de se lidar com a incerteza. Um dos enfoques mais utilizados é a teoria da probabilidade, que é um método sistemático de descrever a aleatoriedade e a incerteza. A teoria apresenta um conjunto de regras para a manipulação e o cálculo de probabilidades. Ela tem sido aplicada em muitas áreas do conhecimento: física, epidemiologia, economia, computação, etc.
7.2 Conceito de probabilidade
Usualmente nos referimos a uma situação em que os desfechos, ou resultados, possuem algum componentes aleatório como um experimento. Um enfoque convencional para a teoria da probabilidade começa com o conceito de espaço amostral, que corresponde a um conjunto de todos os possíveis resultados de um experimento. Subconjuntos do espaço amostral são denominados eventos. Por exemplo, no caso bastante simples em que 3 moedas são lançadas, o espaço amostral dos resultados possíveis será:
S = {hhh; hht; hth; htt; thh; tht; tth; ttt}onde h - cara, t - coroa. Um subconjunto qualquer do espaço amostral é chamado de evento. Por exemplo, podemos definir um evento correspondente a “a segunda moeda é cara” e, nesse caso, teremos o evento
E = {hhh; hht; thh; tht}Quando lançamos um dado, temos para o espaço amostral:
S = {1,2,3,4,5,6}O evento de que o número observado seja menor que 4 é dado pelo subconjunto:
E= {1,2,3}Ao estudarmos uma fonte radioativa, se medirmos o número de partículas emitidas em um minuto, teremos que o espaço amostral será definido por um conjunto infinito de possíveis resultados:
S={0,1,2 ........}Um evento de interesse seria ter em um minuto menos que cinco partículas emitidas:
E = {0,1,2,3,4}Cada elemento do espaço amostral S corresponde a um único resultado. A construção do espaço amostral é feita de modo a nos auxiliar a pensar de forma mais coerente sobre os eventos. Em muitas situações, não há necessidade de definir explicitamente o espaço amostral; em geral é suficiente manipular os eventos por meio de um conjunto de regras sem identificar explicitamente os eventos como um subconjunto do espaço amostral. Por exemplo, ao jogarmos três moedas e observarmos o desfecho {h,h,h} temos então que os seguintes eventos ocorreram: {não coroa}, {pelo menos uma cara}, {mais caras que coroas}. Entretanto o evento {número par de caras} não ocorreu.
A incerteza sobre a ocorrência de um evento é modelada pela probabilidade associada ao mesmo. A probabilidade de ocorrência de um evento E é representada usualmente por P[E] ou P(E).
Possivelmente, a forma mais aceita de se definir probabilidade é a partir da adoção de um conjunto de axiomas. De uma maneira simplificada, a definição axiomática de probabilidade afirma que a probabilidade de um evento é um número, P[E], associado ao evento, que segue um conjunto básico de axiomas ou postulados.
Axiomas da probabilidade:
(P1): \(0 \le P[E] \le 1\), isto é, a probabilidade é um número não negativo entre 0 e 1;
(P2): Para o subconjunto vazio Ø, ou seja, um evento impossível, P[Ø] = 0;
(P3): Para o espaço amostral S, que corresponde ao evento certo, P[S] = 1;
(P4): Se um evento E for dividido em eventos disjuntos, ou mutuamente exclusivos, E1, E2, …, ou seja, se um dos eventos Ei, i = 1, 2, …, ocorrer, os demais não ocorrerão, então a probabilidade do evento E será a soma das probabilidades de cada um dos subeventos Ei, matematicamente expressa por \(P[E] = \sum P[E_i]\)
Para a regra P4, podemos entender o evento E como a união dos eventos E1, E2, … e reescrever o evento de interesse como \(E = E_1 \cup E_2 \cup E_3 \cup ...\), onde o símbolo \(\cup\) corresponde à união.
Em geral, se temos um espaço amostral com N resultados mutuamente exclusivos, então, pelas regras P3 e P4:
\(\begin{aligned} &P[E_1] + P[E_2] + \dots +P[E_N] = P[S] = 1 \end{aligned}\)
Se os eventos são equiprováveis, então P[Ei] = 1/N, i = 1, 2, …, N. Nesse caso, o cálculo das probabilidades se reduz à contagem. Se um evento A consiste de k resultados, a partir do espaço amostral teremos P[A] = k/N. A regra P4 é conhecida como regra da adição para eventos mutuamente exclusivos.
Dois eventos são complementares quando são mutuamente exclusivos e a sua união é o espaço amostral. Se D é um evento, o seu complemento será representado por \(\bar{D}\), ou \(D^c\), ou \(D^-\), e temos a seguinte relação:
\(P[D] = 1 - P[\bar{D}]\)
A definição axiomática não estabelece como as probabilidades de eventos podem ser estimadas. Dependendo da situação, a probabilidade de um evento pode ser estimada por considerações de simetria, considerando todos os resultados de um experimento como equiprováveis e calculando a probabilidade de um evento como o número de resultados favoráveis ao evento dividido pelo número total de resultados possíveis.
Em um lançamento de um dado, por exemplo, se considerarmos que o dado não é viciado, podemos supor que a probabilidade de qualquer uma das faces estar voltada para cima ao cair é 1/6. Assim a probabilidade de ocorrer o evento número ímpar em um lançamento do dado, seria dada por:
\(P(impar) = \frac{3}{6}=0,5=50\%\)
Em outros cenários, a probabilidade pode ser estimada pela proporção da ocorrência de um evento em um certo número de experimentos, ou por algum outro meio. Assim, por exemplo, se 120 cirurgias de um determinado cirurgião foram bem sucedidas em um total de 150 cirurgias realizadas pelo mesmo, podemos estimar a probabilidade de sucesso desse cirurgião como:
\(P(sucesso) = \frac{120}{150}=0,8=80\%\)
Outras regras de probabilidades permitem o cálculo de probabilidades de eventos combinados por meio da operação de união e interseção de conjuntos ou a probabilidade de um evento, sabendo-se que um outro evento ocorreu. As seções seguintes apresentam essas situações.
7.3 Probabilidade da união de eventos
Vamos considerar o lançamento de um dado não viciado e os seguintes eventos:
- evento A: valor par - {2, 4, 6}
- evento B: número primo - {2, 3, 5}
- evento C: valor = 1 - {1}
- evento D: valor > 4 - {5, 6}
As probabilidades associadas aos eventos A, B, C e D podem ser calculadas como:
\(P(A) = \frac{3}{6} = \frac{1}{2}\)
\(P(B) = \frac{3}{6} = \frac{1}{2}\)
\(P(C) = \frac{1}{6}\)
\(P(D) = \frac{2}{6} = \frac{1}{3}\)
Os eventos C e D não possuem nenhum elemento em comum, logo eles são mutuamente exclusivos, e a probabilidade da união dos eventos C e D, {1, 5, 6}, é dada pela soma das probabilidades dos eventos C e D, pela propriedade P4 acima:
\(P(C \cup D) = P(C) + P(D) = \frac{1}{6} + \frac{2}{6} = \frac{1}{2}\)
Os eventos A e B não são mutuamente exclusivos. A interseção de A e B, representada pela notação \(A \cap B\), é o conjunto formado pelos elementos comuns a A e B. Nesse exemplo:
\(A \cap B = \{2\}\)
Para dois eventos que não são mutuamente exclusivos, a probabilidade da união pode ser calculada pela seguinte expressão:
\[\begin{align} &P(A \cup B) = P(A) + P(B) - P(A \cap B) \tag{7.1} \end{align}\]
Assim, no exemplo acima, temos:
\(P(A\cup B) = P(A) + P(B) - P(A \cap B) = \frac{1}{2} + \frac{1}{2} - \frac{1}{6} = \frac{5}{6}\)
A fórmula para a probabilidade da união de dois eventos pode ser facilmente entendida a partir do diagrama de Venn (figura 7.1).
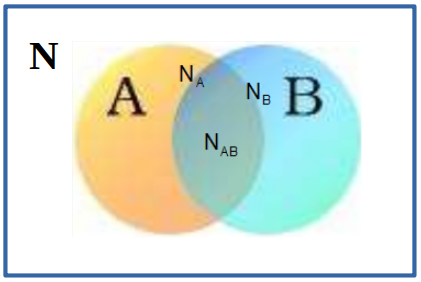
Figura 7.1: Dois eventos A e B. NA significa o número de maneiras (eventos elementares) que o evento A pode ocorrer, NB significa o número de maneiras que o evento B pode ocorrer, NAB significa o número de maneiras que o evento A e B ocorrem simultaneamente. N é o número total de eventos elementares distintos no espaço amostral.
A partir dessa figura, temos:
\(\begin{aligned} &P(A) = \frac{N_A}{N} \\ &P(B) = \frac{N_B}{N} \\ &P(A\cap B) = \frac{N_{AB}}{N} \\ &P(A \cup B) = \frac{\text{Número de eventos elementares em}\ A \cup B}{N}=\frac{N_A+N_B-N_{AB}}{N} \\ &P(A \cup B) = \frac{N_A}{N} + \frac{N_B}{N} - \frac{N_{AB}}{N} \end{aligned}\)
Logo:
\(\begin{aligned} P(A \cup B) = P(A) + P(B) - P(A \cap B) \end{aligned}\)
A razão para a subtração de NAB é que NA inclui os eventos elementares que estão em A mas não estão em B e os eventos elementares que também estão em B, e NB inclui os eventos elementares que estão em B mas não estão em A e os eventos elementares que também estão em A. Assim, ao somarmos NA + NB, estamos somando NAB duas vezes. Logo é preciso subtrair NAB uma vez da soma NA + NB.
Para A e B serem eventos disjuntos ou mutuamente exclusivos, a intersecção desses eventos deve ser o conjunto vazio, isto é, dois eventos disjuntos nunca podem ocorrer juntos.
Para três eventos A, B e C, a probabilidade da união dos três eventos é dada por:
\(P(A \cup B \cup C) = P(A) + P(B) + P(C)-P(A\cap B )-P(B \cap C)-P(A \cap C) + P(A \cap B \cap C)\)
Essa fórmula pode também facilmente ser entendida por meio de um diagrama de Venn com três eventos A, B e C. A extensão dessa fórmula para n eventos E1, E2, E3, …, En pode ser obtida por indução matemática.
Exemplo 1: Sendo P[C] = 0,48 a probabilidade de que um médico se encontre em seu consultório e P[D] = 0,27 a probabilidade de que ele se encontre no hospital, pergunta-se: qual a probabilidade de que ele não se encontre em nenhum desses dois lugares P[A]?
Assumindo que esse médico não tenha consultório no hospital, os eventos são mutuamente exclusivos, já que o médico não pode estar no hospital e no consultório ao mesmo tempo. Assim:
\(P(C \cup D) = P(C)+P(D) = 0,75\)
e, portanto, temos como calcular a probabilidade do evento desejado:
\(P(A) = P[(C \cup D)^-] = 1- P(C \cup D) = 1 - 0,75 = 0,25\)
7.4 Probabilidade condicional
Os conteúdos desta seção e da seção 7.5 podem ser visualizados neste vídeo.
Nem todos os problemas de cálculo de probabilidades são resolvidos como nos exemplos anteriores, dividindo o evento em partes cujas probabilidades conhecemos e, então, somando as probabilidades. Em geral a obtenção das probabilidades depende do que é conhecido e do que foi aprendido ou assumido sobre a situação que estamos trabalhando. Por exemplo, poderíamos ter representado o exemplo anterior sobre o lançamento de dado e a obtenção de um resultado ímpar como:
P[resultado = ímpar | dado não é viciado]para indicar que a obtenção da probabilidade é condicionada a algumas informações (ou hipóteses). A barra vertical é lida como supondo que, e nos referimos à probabilidade de ocorrer um resultado ímpar em um lançamento de um dado, supondo que o dado não é viciado. Se a informação condicionante não varia durante a análise, então usualmente não temos que nos preocupar com o componente supondo que da probabilidade condicional. Entretanto, se a informação condicionante varia, então essa notação é fundamental na análise.
Vamos considerar um exemplo simples:
Exemplo 2: Seja um lote de 100 peças, com 20 peças defeituosas e 80 peças boas. Suponhamos que escolhamos duas peças aleatoriamente desse lote sem reposição, ou seja, retiramos uma peça aleatoriamente e, a seguir, retiramos aleatoriamente outra peça das restantes no lote.
Sejam dois eventos A e B, definidos como:
A = {\(1^a\) peça é defeituosa },
B = {\(2^a\) peça é defeituosa}
Temos que: \(P(A) = \frac{20}{100} = \frac{1}{5}\)
Vamos calcular a probabilidade de B ocorrer dado que A ocorreu, ou seja, a primeira peça retirada é defeituosa. Denotamos por \(P(B|A)\) a probabilidade condicional de o evento B ocorrer quando A tiver ocorrido: \[P(B|A)= 19/99\]
A probabilidade das duas peças serem defeituosas pode ser calculada como:
\[P(A \cap B) = \frac {{20 \choose 2}}{{100 \choose 2}} = \frac{1}{5}\ .\ \frac{19}{99}= P(A)P(B|A)\]
Assim podemos usar a seguinte definição de probabilidade condicional:
Se A e B são eventos, então:
\[\begin{align} P(B|A) = \frac{P(A \cap B)}{P(A)} \tag{7.2} \end{align}\]
O diagrama de Venn (figura 7.2) nos ajuda a compreender a razão da definição (7.2).

Figura 7.2: Diagrama de Venn para visualizar o cálculo da probabilidade condicional.
Seja N o número de eventos elementares no espaço amostral. Então:
\(P(B|A) = \frac{N_{AB}}{N_A}\) e \(P(A) = \frac{N_A}{N}\)
e, nesse caso, temos que, em \(N_A\) vezes em que A ocorreu, \(N_{AB}\) vezes A e B ocorreram, logo:
\[P(A \cap B) = \frac{N_{AB}}{N} = \frac{N_{AB}}{N_A}\ .\ \frac{N_{A}}{N}= P(B|A).P(A) \]
\[Logo:\ P(B|A) = \frac{P(A \cap B)}{P(A)}\]
A expressão \[P(A \cap B) = P(B|A).P(A)\]
é conhecida como regra da multiplicação.
Exemplo 3: Vamos considerar os resultados apresentados pelo estudo de Hjerkind, Stenehjem e Nilsen (Hjerkind, Stenehjem, and Nilsen 2017), que avaliou a associação entre a adiposidade e a atividade física com o diabetes mellitus por meio de um estudo de coortes. A tabela 7.1 é uma versão simplificada dos resultados desse estudo, que mostra a associação entre dois níveis de atividade física e diabetes mellitus entre os homens.
| Atividade Física | Sim | Não | Total |
|---|---|---|---|
| Inativo | 73 | 1875 | 1948 |
| Exercita 4+ vezes/semana | 45 | 1836 | 1881 |
| Total | 118 | 3711 |
Supondo que o estudo tenha uma boa validade interna e que não houvesse outros fatores que influenciassem o desfecho, qual a probabilidade de um homem com o perfil da população considerada nesse estudo desenvolver diabetes mellitus se ele for inativo?
Nesse caso, estamos interessados na P(diabetes | Inativo), ou seja, a probabilidade de um desfecho de diabetes dado que a pessoa é inativa. Analogamente, poderíamos estar interessados na probabilidade P(diabetes | Exercita 4 ou mais vezes por semana), ou seja, a probabilidade de um desfecho de diabetes dado que a pessoa exercita 4 ou mais vezes na semana.
A partir dos dados tabulados, a P(diabetes | Inativo) é estimada dividindo-se o número de pessoas inativas que tiveram diabetes pelo total de pessoas inativas acompanhadas.
\(P(diabetes | inativo) = \frac{73}{1948}= 0,037\)
\(P(diabetes | Exercita \ge 4)\) é estimada dividindo-se o número de pessoas que exercitam 4 ou mais vezes por semana e que tiveram diabetes pelo total de pessoas que exercitam 4 ou mais vezes por semana.
\(P(diabetes | Exercita \ge 4) = \frac{45}{1881}= 0,024\)
7.5 Eventos independentes
Voltando ao exemplo do lote de peças defeituosas (exemplo 2), vamos supor agora que a retirada das peças é com reposição, ou seja, a segunda peça é retirada após a primeira peça retirada ser reposta ao lote. Considerando os eventos A e B, definidos como:
A = {1a peça é defeituosa },
B = {2a peça é defeituosa}
Com reposição, temos que:
\[P(A) = P(B) = \frac{20}{100}= \frac{1}{5} \]
\(P(B|A) = P(B|\bar{A})= P(B)\), ou seja, a probabilidade de ocorrência da segunda peça ser defeituosa independe do fato de a primeira ser defeituosa ou não
\[P(A \cap B) = P(A).P(B|A) = P(A). P(B)\]
Dizemos que os eventos A e B são condicionalmente independentes se:
P[B|A] = P[B] e, nesse caso:
\[\begin{equation} P(A \cap B) = P(A) P(B) \tag{7.3} \end{equation}\]
A independência de eventos é uma hipótese frequentemente usada na modelagem estatística. Ela permite reduzir considerações sobre sequências complexas de eventos a uma análise de cada evento isoladamente.
7.6 Teorema de Bayes
O conteúdo desta seção pode ser visualizado neste vídeo.
O teorema de Bayes consiste de uma manipulação da regra da multiplicação, reescrita de duas maneiras equivalentes:
\(P[A \cap B] = P[A] P[B|A] = P[B] P[A|B]\)
Logo temos:
\[\begin{equation} P[B|A] = \frac{P[B]P[A|B]}{P[A]} \tag{7.4} \end{equation}\]
Esse é o teorema de Bayes, o qual permite o cálculo de P[B|A] se conhecermos P[A], P[B] e P[A|B].
Exemplo 4: Vamos considerar o estudo de Malacarne et al. (Malacarne et al. 2019), que avaliou o desempenho de testes para o diagnóstico de tuberculose pulmonar em populações indígenas no Brasil. Os resultados para o teste rápido molecular (TRM) em comparação à cultura de escarro (teste padrão) para todas as amostras de escarro combinadas são mostrados na tabela 7.2.
| Teste Rápido Molecular (TRM) | Com TB (D) | Sem TB (\(\bar{D}\)) | Totais |
|---|---|---|---|
| Teste positivo (T+) | 54 | 7 | 61 |
| Teste negativo (T-) | 4 | 401 | 405 |
| 58 | 408 | 466 |
A partir dessa tabela, podemos obter um conjunto de informações importantes referentes à avaliação do uso do teste rápido molecular (TRM):
Verdadeiros positivos: são os pacientes onde tanto o TRM quanto a cultura de escarro indicaram tuberculose pulmonar (54 pacientes);
Verdadeiros negativos: são os pacientes onde tanto o TRM quanto a cultura de escarro não indicaram tuberculose pulmonar (401 pacientes);
Falsos positivos: são os pacientes que o TRM indicou tuberculose pulmonar, mas a cultura de escarro deu negativo (7 pacientes);
Falsos negativos: são os pacientes que o TRM deu negativo, mas a cultura de escarro indicou tuberculose pulmonar (4 pacientes);
Sensibilidade: é a indicação da capacidade de o exame (TRM) de identificar pacientes que de fato tenham a condição e corresponde a uma probabilidade condicional
\[P(T^+|D) = 54/58 = 0,931\]Especificidade: corresponde à capacidade de o exame de rejeitar corretamente pacientes não portadores da condição, sendo também uma probabilidade condicional
\[P(T^-|\bar{D}) = 401/408 = 0,983\]
- Finalmente uma informação fundamental é sabermos que, uma vez tendo-se um resultado positivo, qual é a probabilidade de que o paciente tenha a condição, isto é, qual é a probabilidade de um paciente ter tuberculose pulmonar, dado que o exame foi positivo, P(D|T+). Devido à forma como o estudo foi realizado, essa probabilidade não pode ser calculada somente a partir da tabela 7.2 sem o conhecimento da prevalência da doença na população de interesse, P(D), também chamada de probabilidade pré-teste.
Suponhamos agora que a prevalência da tuberculose numa população é P(D) = 0,1 = 10%. Como poderíamos obter P(D|T+)?
Para efetuarmos esse cálculo, temos que utilizar o teorema de Bayes.
Temos como informações disponíveis: a probabilidade pré-teste de ocorrência da doença P(D), a probabilidade de termos um resultado positivo dado que o indivíduo tenha a doença P(T+|D), e também a probabilidade de que o teste dê um resultado positivo se o indivíduo não estiver com a doença P(T+|D-).
A partir da regra da multiplicação, temos:
\(P(D \cap T^+) = P(T^+)\ .\ P(D|T^+) = P(D)\ .\ P(T^+|D)\)
onde D é o evento ter a doença e T+ é ter um resultado positivo no exame. Com base nessa expressão, podemos escrever:
\[\begin{equation} P(D | T^+) = \frac{P(D)\ .\ P(T^+|D)}{P(T^+)} \tag{7.5} \end{equation}\]
Observamos que está faltando um dado importante, que é a probabilidade de termos um resultado positivo, P(T+). Uma forma de obtermos essa probabilidade é escrevermos P[T+] como:
\[\begin{equation} P(T^+) = P(T^+ \cap D) + P(T^+ \cap D^-) = P(D)\ P(T^+|D) + P(D^-)\ P(T^+|D^-) \tag{7.6} \end{equation}\]
Essa expressão pode ser melhor compreendida a partir da figura 7.3. Nesse diagrama, podemos ver que o evento T+ pode ser expresso pela união das interseções de T+ com o evento D e com o seu complemento \((\bar{D})\), respectivamente.
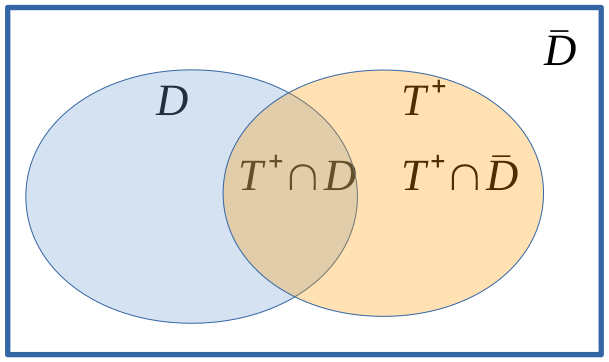
Figura 7.3: Diagrama de Venn que ilustra como obter a probabilidade de um evento T+ a partir da interseção de T+ com dois outros eventos complementares.
Temos:
\(P(D) = 0,1\)
\(P(\bar{D}) = 1 - P(D) = 1 - 0,1 = 0,9\)
\(P(T^+|D) = 0,931\)
\(P(T^-|\bar{D}) = 0,983\)
\(P(T^+|\bar{D})=1-P(T^-|\bar{D}) = 1 - 0,983 = 0,017\)
Substituindo os valores acima na expressão (7.6), temos:
\(P[T^+]= 0,1\ .\ 0,931 + (1 - 0,1)\ .\ 0,017 = 0,1085\)
Finalmente: \(P[D|T^+] = \frac{0,1\ .\ 0,931}{0,1085}\)= 0,858 = 85,8%
Essas e outras métricas para avaliação de testes diagnósticos serão tema do capítulo 12.
7.7 Exercícios
- Em uma determinada população de mulheres, 4% tiveram câncer de mama, 20% são fumantes e 3 por cento são fumantes e tiveram câncer de mama. Uma mulher é selecionada aleatoriamente da população. Qual é a probabilidade de ela ter câncer de mama ou fumar ou ambos?
- Em um hospital, os centros cirúrgicos I, II e III são responsáveis por 37%, 42% e 21% do total de cirurgias. Se 0,6% das infecções hospitalares são oriundas do centro cirúrgico I, e as percentagens para os centros cirúrgicos II e III são respectivamente 0,4% e 1,2%, qual é a probabilidade de que um paciente com infecção hospitalar tenha feito cirurgia no centro cirúrgico III?
Seja o evento A a infecção hospitalar e sejam os eventos B1, B2 e B3 correspondendo a pacientes operados na sala I, II e III, respectivamente. Temos:
P(B1) = 0,37, P(B2) = 0,42, P(B3) = 0,21
P(A|B1) = 0,006
P(A|B2) = 0,004
P(A|B3) = 0,012
Suponha que 0,5% (0,005) da população apresentam uma doença D. Um teste para detectar essa doença existe, mas não é perfeito. Para pessoas com a doença D, o teste erra o diagnóstico 2% das vezes (falsos negativos). Para pessoas que não possuem a doença, ele indica a doença em 3% das vezes (falsos positivos).
- Determine a probabilidade de que uma pessoa escolhida aleatoriamente da população terá um teste positivo.
- Se o teste for positivo, qual é a probabilidade que a pessoa tenha D.