14 Intervalo de confiança
14.1 Introdução
Os conteúdos desta seção e das seções 14.2 e 14.3 podem ser visualizados neste vídeo.
De acordo com a interpretação frequentista, um intervalo de confiança para um determinado parâmetro da população mostra um intervalo de valores do verdadeiro parâmetro da população compatíveis com os dados da amostra, com um certo nível de confiança, seja o parãmetro a média de uma determinada distribuição, o risco relativo, a razão de chances, a variância, etc. O cálculo do intervalo de confiança é um dos principais resultados de uma análise estatística.
O capítulo 6 mostrou um exemplo de cálculo de um intervalo de confiança para a diferença de médias entre dois grupos, utilizando o método de randomização. Este capítulo aprofundará o conceito de intervalo de confiança e mostrará como calculá-lo em algumas situações onde a distribuição dos dados é conhecida. Inicialmente, iremos mostrar o cálculo e a interpretação de um intervalo de confiança para a média de uma população que segue uma distribuição normal com variância conhecida.
Intervalos de confiança para a média de uma distribuição normal quando a variância da população não é conhecida nos leva à distribuição t de Student. Finalmente serão apresentados intervalos de confiança para a variância de uma distribuição normal e a probabilidade de um evento de Bernoulli.
14.2 Intervalo de confiança - IC
Neste capítulo, vamos adotar a seguinte convenção: zp significa o valor da variável aleatória Z que segue a distribuição normal padrão, N(0,1), para o qual P(z \(\leq\) zp) = p, ou seja, a área sob a curva normal padrão à esquerda de zp é igual a p. Assim, para p = 0,01 (1%), z0,01 = -2,33. Como a curva normal padrão é simétrica em torno de 0, a área sob a curva acima de z1-p é também igual a p (figura 14.1).
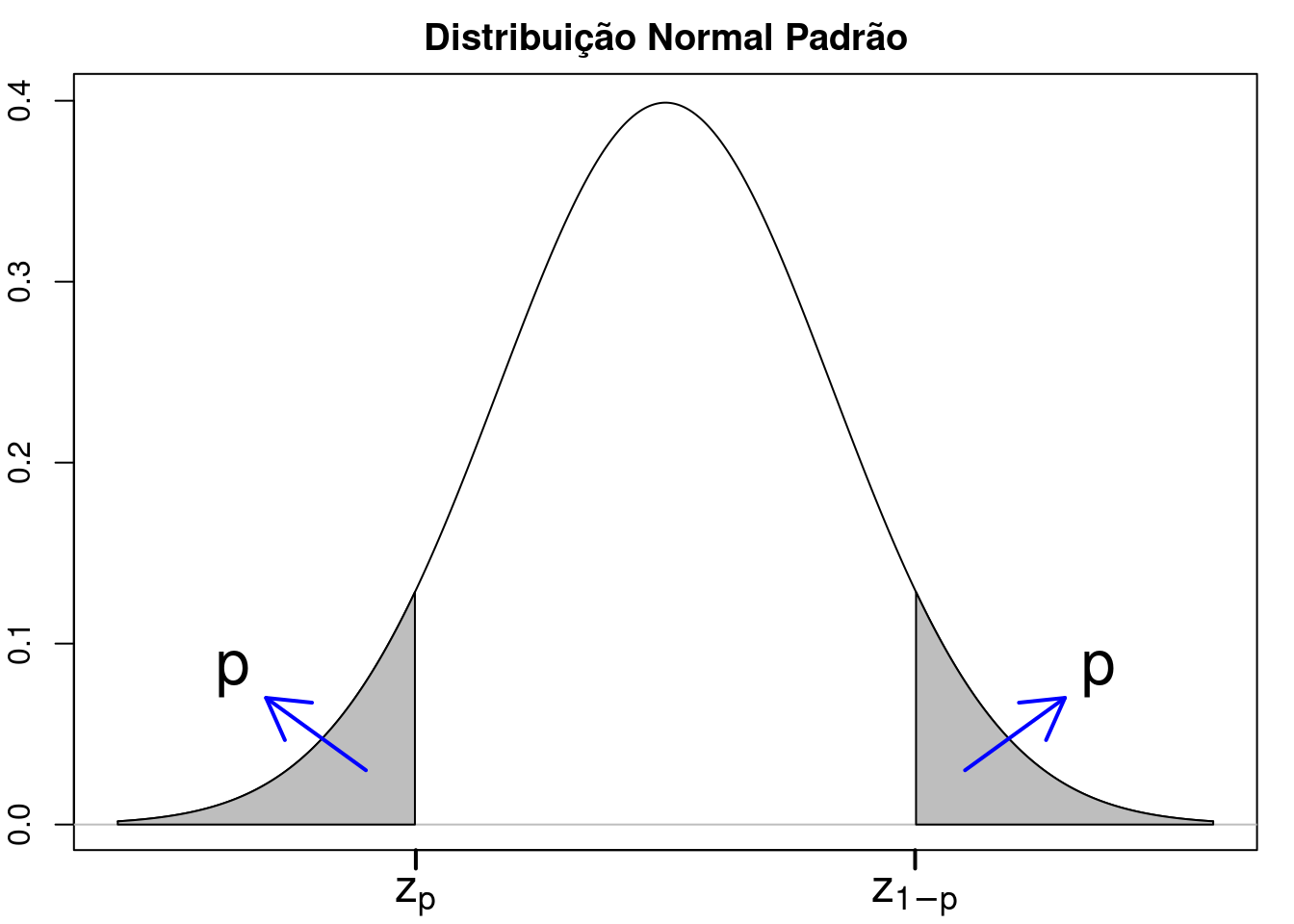
Figura 14.1: Curva normal padrão: p é a área sob a curva normal à esquerda de zp ou à direita de z1-p.
Para introduzir o conceito de intervalo de confiança de um parâmetro populacional, vamos partir do exemplo a seguir.
Exemplo 1: Vamos supor que a glicemia de jejum de uma população de pessoas não diabéticas siga a distribuição normal, com desvio padrão igual a 16, mas não conhecemos o valor da média dessa população. Também vamos supor que extraimos uma amostra aleatória de tamanho 36 da população de pessoas não diabéticas e obtivemos a média amostral da glicemia de jejum igual a 92 mg/dl.
Então: \(\bar{x} = 92\) mg/dl, n = 36 e \(\sigma = 16\) mg/dl.
Como podemos estimar a média da população com um certo nível de confiança estabelecido a priori?
Para uma população com uma distribuição normal padrão, dado um valor \(\alpha\ (0 \leq \alpha \leq 1)\), podemos obter o intervalo \((z_{\alpha/2}, z_{1-\alpha/2})\) que conterá com probabilidade \((1 - \alpha)\) o valor de um elemento extraído aleatoriamente dessa população (figura 14.2). Para a distribuição normal padrão, \(z_{\alpha/2} = - z_{1-\alpha/2}\).
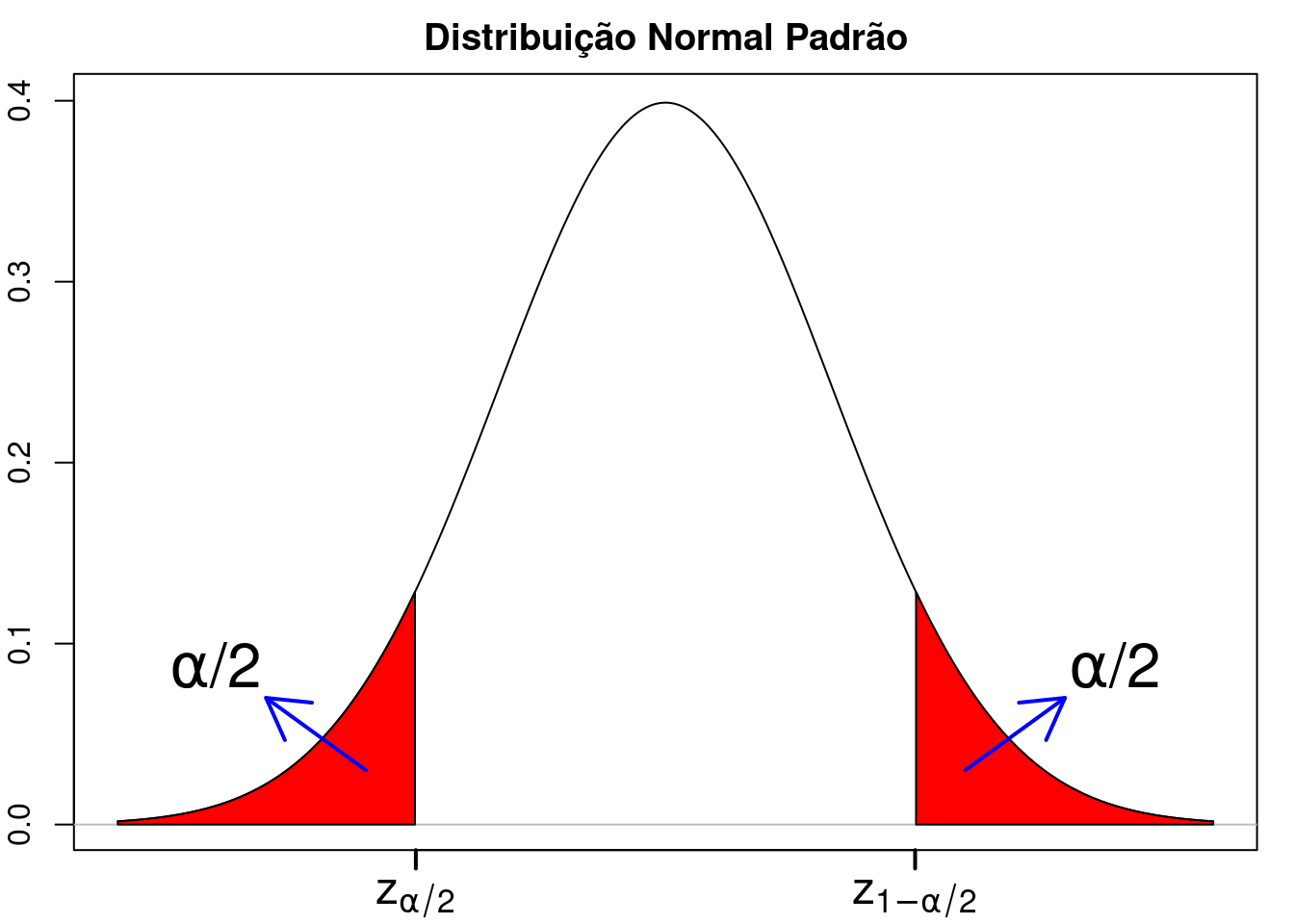
Figura 14.2: Distribuição normal padrão. A área sob a curva compreendida no intervalo \((z_{\alpha/2}, z_{1-\alpha/2})\) é igual a \((1 - \alpha)\) e representa a probabilidade de se extrair um elemento da população e obter um valor no intervalo \((z_{\alpha/2}, z_{1-\alpha/2})\), \(z_{\alpha/2} = - z_{1-\alpha/2}\). Semelhante à figura 14.1, com p substituído por \(\alpha/2\).
Usando a função qnorm no R, podemos obter os valores de \(z_{1-\alpha/2}\) para qualquer valor de \(\alpha\) entre 0 e 1. Por exemplo, para \(\alpha = 0,05 (5\%)\), o valor de z0,975 é igual a 1,96:
## [1] 1.959964Outros valores de \(\alpha\) comumente usados são 0,1 (10%) e 0,01 (1%). Os valores correspondentes de z0,95 \((\alpha = 10\%)\) e z0,995 \((\alpha = 1\%)\) são:
## [1] 1.644854 2.575829A tabela 14.1 resume os três valores de \(\alpha\ e\ z_{1-\alpha/2}\) obtidos acima.
| \(\alpha\) | \(z_{1-\alpha/2}\) |
|---|---|
| 1% | 2,58 |
| 5% | 1,96 |
| 10% | 1,64 |
Podemos mapear áreas sob o gráfico de uma distribuição normal genérica com média \(\mu\) e desvio padrão \(\sigma\) para áreas sob o gráfico da distribuição normal padrão por meio da expressão:
\[\begin{align} Z = \frac{X-\mu}{\sigma} \tag{14.1} \end{align}\]
Assim o intervalo \(z_{\alpha/2} \le Z \le z_{1-\alpha/2}\) irá ser mapeado para o intervalo
\[\begin{align} z_{\alpha/2} \le \frac{X-\mu}{\sigma} \le z_{1-\alpha/2} \end{align}\]
\[\begin{align} \mu + z_{\alpha/2} \sigma \le X \le \mu + z_{1-\alpha/2} \sigma \Rightarrow \mu - z_{1-\alpha/2} \sigma \le X \le \mu + z_{1-\alpha/2} \sigma \tag{14.2} \end{align}\]
Portanto a probabilidade de extrairmos um elemento da população com distribuição \(N(\mu, \sigma^2)\) e o valor desse elemento pertencer ao intervalo \([\mu - z_{1-\alpha/2} \sigma,\ \mu + z_{1-\alpha/2} \sigma]\) é \((1 - \alpha)\%\).
Voltando ao exemplo 1, conforme vimos no capítulo anterior, uma distribuição populacional possui parâmetros os quais podem ser estimados a partir de estatísticas obtidas a partir de amostras. Também vimos que toda estatística amostral tem associada uma distribuição amostral. Para uma população que possui uma distribuição normal \(N(\mu, \sigma^2)\) com média \(\mu\) e desvio padrão \(\sigma\), a distribuição da média amostral para amostras de tamanho n será \(N(\mu, \sigma^2/n)\).
Substituindo \(\sigma\) por \(\frac{\sigma}{\sqrt{n}}\) na expressão (14.2), obtemos o intervalo:
\[\begin{align} \mu - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \le \bar{X} \le \mu + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \tag{14.3} \end{align}\]
A área sob o gráfico da distribuição da média amostral compreendida no intervalo (14.3) é a probabilidade \(\boldsymbol{(1 - \alpha)\%}\) de extrairmos uma amostra de tamanho n da população e obtermos uma média amostral dentro desse intervalo.
Então:
\[\begin{align} P\left(\mu - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \bar{X} \leq \mu + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\right) = (1-\alpha)\% \tag{14.4} \end{align}\]
Como no exemplo 1, e na maioria das situações, não conhecemos a média da população, podemos reescrever a expressão (14.4) como abaixo:
\[\begin{align} P\left(\bar{X} - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right) = (1-\alpha)\% \tag{14.5} \end{align}\]
A expressão (14.5) deve ser interpretada da seguinte forma: ela indica que a probabilidade de o intervalo aleatório (14.6) a seguir conter a média \(\mu\) da população é \((100 - \alpha)\%\):
\[\begin{align} \left[\bar{X} - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}, \bar{X} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right] \tag{14.6} \end{align}\]
Esse intervalo é o intervalo de confiança ao nível de \(\boldsymbol{(100 - \alpha)\%}\) para a média da população.
14.3 Interpretação do intervalo de confiança
O intervalo de confiança \((100 - \alpha)\%\) para um parâmetro consiste em um intervalo aleatório que possui a propriedade de conter o valor real desse parâmetro com uma probabilidade de \((100 - \alpha)\%\). O termo aleatório nessa interpretação indica que, antes de realizarmos a amostragem e calcularmos o intervalo de confiança de acordo com o procedimento apropriado, haverá uma probabilidade de \((100 - \alpha)\%\) de o intervalo vir a conter o real valor do parâmetro de interesse.
A expressão (14.6) é utilizada na aplicação Intervalos de confiança (figura 14.3), que nos ajuda a interpretar o intervalo de confiança. A explicação a seguir sobre essa aplicação reproduz o texto do capítulo 6, seção 6.9.
A aplicação Intervalos de confiança calcula e exibe intervalos de confiança para a média de uma distribuição normal, a partir de um certo número de amostras extraídas dessa distribuição. Os parâmetros da distribuição normal, bem como o nível de confiança, o tamanho de cada amostra e o número de amostras são especificados pelo usuário. O painel principal é atualizado sempre que o usuário pressiona o botão Reamostrar (mais intervalos de confiança são exibidos) ou Limpar (limpa a tela).
Figura 14.3: Aplicação que calcula e exibe intervalos de confiança para a média de uma distribuição normal calculados a partir de um certo número de amostras extraídas dessa distribuição.
A figura 14.4 exibe intervalos de confiança para 50 amostras de tamanho 10 de uma distribuição normal N(80, 400). Para cada amostra, foi calculado o intervalo de confiança ao nível de 95% conforme a expressão (14.6), com \(z_{1-\alpha/2} = 1,96\) e \(\sigma = 20\). Os 50 intervalos de confiança são exibidos no painel principal da figura.
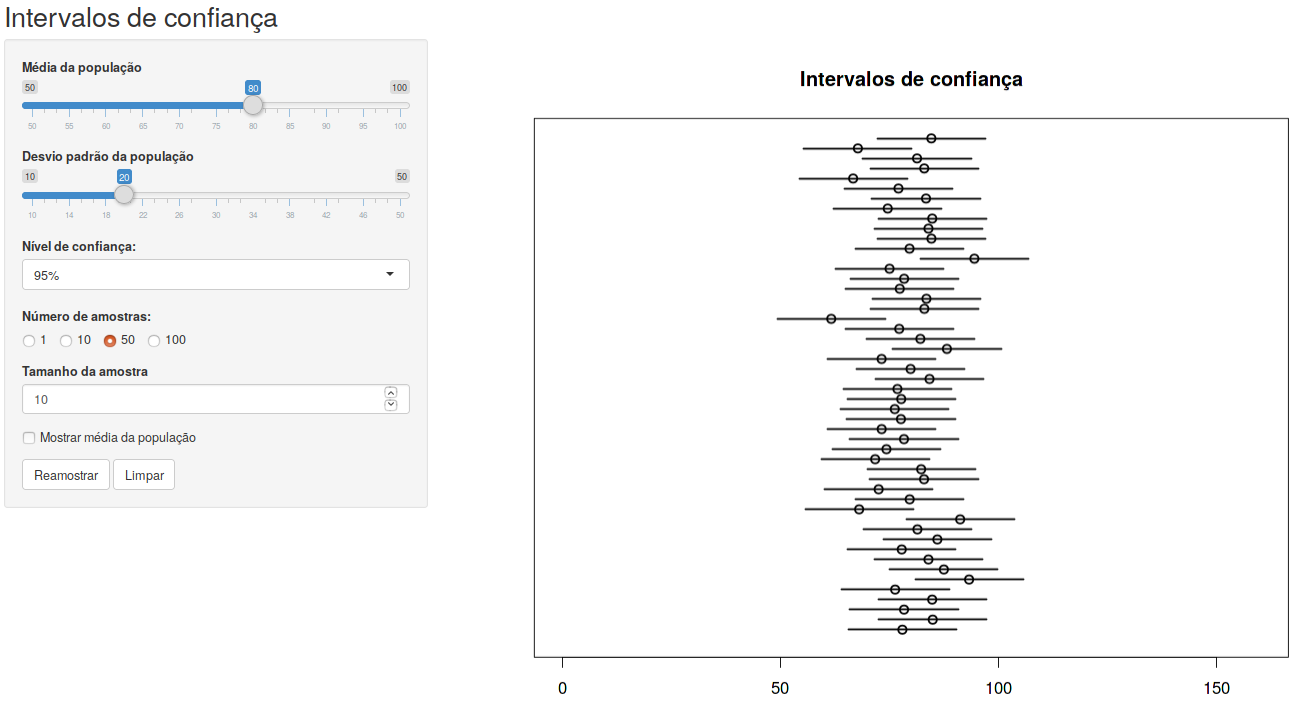
Figura 14.4: Intervalos com 95% de confiança para a média de uma distribuição normal N(80, 400), calculados a partir de 50 amostras de tamanho 10.
Ao selecionarmos a opção Mostrar média da população na aplicação, uma linha preta, indicando a média real da população, é exibida, e duas linhas verticais em vermelho indicam distâncias iguais a \(z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\) acima e abaixo da média da distribuição (figura 14.5). Para cada intervalo de confiança, o centro com uma marcação representa a média da respectiva amostra. Observem que a maioria dos intervalos de confiança contêm a média da distribuição, mas alguns deles (em vermelho) não contêm a média.
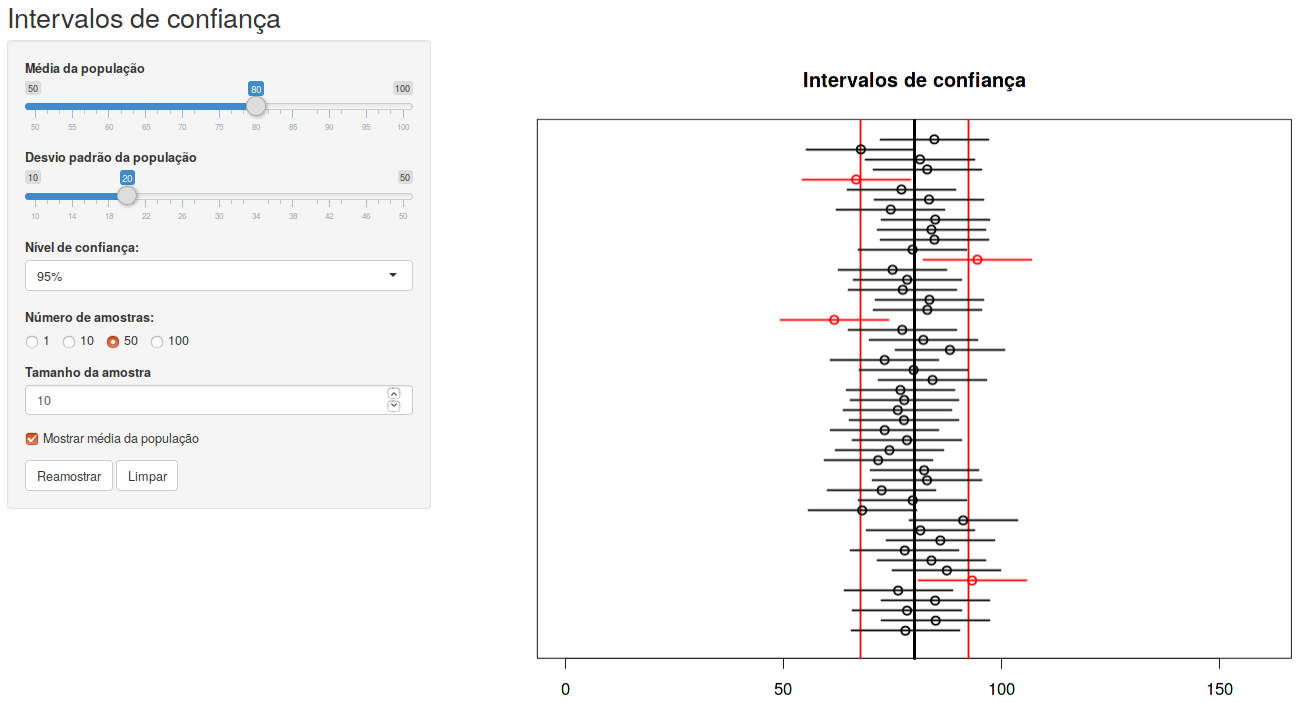
Figura 14.5: Figura 14.4 com linhas que mostram a média real da população (linha vertical preta) e indicam distâncias iguais a \(z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}}\) acima e abaixo da média da distribuição (linhas verticais vermelhas).
É de se esperar que nem sempre o intervalo de confiança contenha o valor real do parâmetro que ele estima. No exemplo da figura 14.5, o nível de confiança é de 95%. Isso significa que, se extraíssemos um número infinito de amostras aleatórias da população e calculássemos os respectivos intervalos de confiança, em 95% das vezes o intervalo de confiança irá incluir a média real da população e em 5% das vezes, o intervalo de confiança não irá incluir a média. Isso equivale a dizer que, a cada 100 intervalos de confiança calculados, em média 5 (5%) não conterão a média da distribuição. Na figura 14.5, 4 intervalos em 50 não contêm a média real da distribuição.
A figura 14.6, mostra o uso da aplicação com a mesma distribuição normal da figura 14.3, com o mesmo número de amostras, mas com três tamanhos amostrais diferentes (1, 10 e 50). Observem que a precisão dos intervalos de confiança aumenta à medida que o tamanho das amostras aumenta de 1 para 10 e de 10 para 50. Isso é de se esperar, porque o erro padrão \(\frac{\sigma}{\sqrt{n}}\), utilizado no cálculo do intervalo de confiança, diminui com n.
O leitor deve experimentar com diferentes níveis de confiança, número de amostras, tamanhos amostrais e parâmetros da distribuição normal.
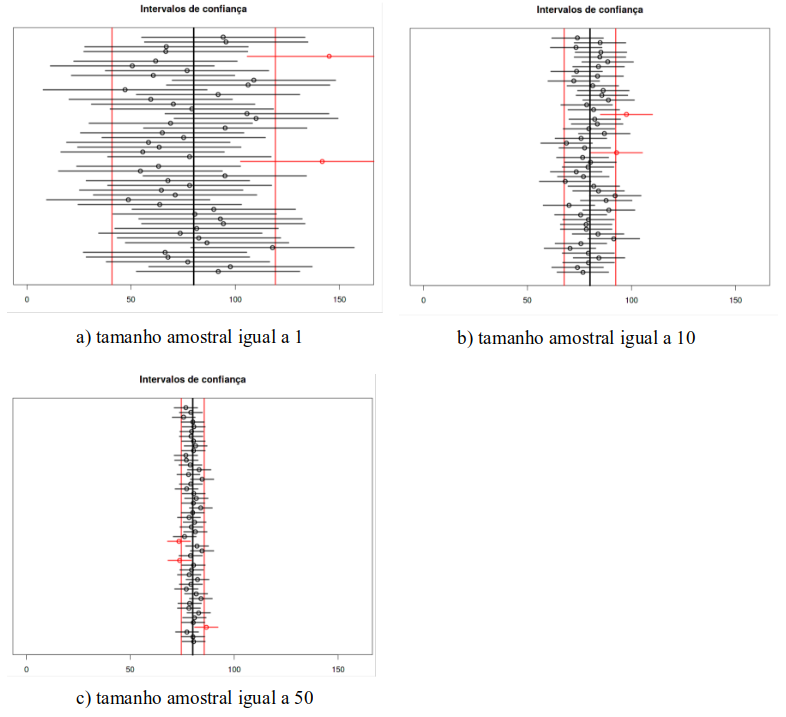
Figura 14.6: Intervalos de confiança para diferentes tamanhos de amostra (a-1, b-10, c-50).
Para qualquer estudo específico, não é possível garantir que o intervalo de confiança calculado contenha o parâmetro real da população.
Resumindo esta seção, podemos interpretar o intervalo de confiança da seguinte forma:
Dado um nível de confiança estabelecido a priori \(\boldsymbol{(100-\alpha)}\)%, temos uma confiança de \(\boldsymbol{(100-\alpha)}\)% que o IC contenha o real valor do parâmetro estudado.
Essa confiança deve ser interpretada no sentido de que, se repetíssemos o estudo um número infinito de vezes e, em cada vez, calculássemos o IC, em \((100-\alpha)\)% das vezes o IC conteria o real valor do parâmetro estudado.
Voltando ao exemplo 1, substituindo os valores
\(\bar{x} = 92\) mg/dl, n = 36 e \(\sigma = 16\) mg/dl
na expressão (14.6), temos que o intervalo de confiança ao nível de 95% para a média da glicemia de jejum de nossa população de pessoas não diabéticas é dado por:
\(92 - 1,96\ .\ 16/6 \leq \mu \leq 92 + 1,96\ .\ 16/6\)
\[\begin{align} 86,8 &\leq \mu \leq 97,2 \ \ ( mg/dl)\tag{14.7} \end{align}\]
Se desejássemos o intervalo de confiança ao nível de 99%, bastaria substituir na expressão (14.6) os valores de \(\bar{x},\ n,\ \sigma\ e\ z_{0,995}\).
14.4 IC para a média quando a variância não é conhecida
O conteúdo desta seção pode ser visualizado neste vídeo.
Recordando mais uma vez, para uma população que possui uma distribuição normal \(N(\mu, \sigma^2)\) com média \(\mu\) e desvio padrão \(\sigma\), a distribuição da média amostral para amostras de tamanho n será \(N(\mu, \sigma^2/n)\). Isso significa que a distribuição da variável aleatória
\(\begin{aligned} &\ Z = \frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \end{aligned}\)
possui a distribuição N(0, 1). Isso justifica a utilização de \(z_{1-\alpha/2}\) na expressão (14.6) para o cálculo do intervalo de confiança.
O que acontece quando não conhecemos a variância da população, que é o caso mais comum? Nesse caso, podemos estimar \(\sigma^2\) por \(S^2\) , onde:
\(\begin{aligned} S^2 =\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2 \end{aligned}\),
porém a distribuição da variável aleatória
\(\begin{aligned} T =\frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}} \end{aligned}\)
não segue a distribuição normal padrão N(0,1). Na realidade, a variável aleatória T segue uma distribuição conhecida como t de Student, devido ao fato de essa distribuição ter sido publicada por William Gosset, que a publicou sob o pseudônimo de Student.
Matematicamente, a distribuição t de Student é dada pela fórmula:
\[\begin{align} T : f(t) = \frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu\pi}\ \Gamma(\frac{\nu}{2})}{\left(1+\frac{t^2}{\nu}\right)}^{-\frac{\nu+1}{2}} \tag{14.8} \end{align}\]
onde \(\Gamma\) é a função Gama e \(\nu\) é o número de graus de liberdade.
A função Gama é dada pela seguinte integral:
\[\begin{align} \Gamma(\alpha) = \int_0^\infty {t^{\alpha - 1}}e^{-t}dt \end{align}\]
O valor esperado de T é igual a zero (E[T] = 0) e seu desvio padrão é maior 1.
A variável aleatória T segue a distribuição t de Student com n–1 graus de liberdade.
A figura 14.7 mostra o gráfico da distribuição normal padrão superposto ao gráfico da distribuição t de Student com \(\nu = 1\). É possível observar que o gráfico da distribuição t de Student com 1 grau de liberdade é menos concentrado em torno da média do que o gráfico da distribuição normal padrão e se espalha mais para as laterais.
A figura 14.8 mostra o gráfico da distribuição normal padrão superposto aos gráficos da distribuição t de Student com \(\nu = 1,\ 5,\ 15\ e\ 30\), respectivamente. Observem que o gráfico da distribuição t de Student se aproxima cada vez mais do gráfico da distribuição normal padrão à medida que o número de graus de liberdade aumenta.
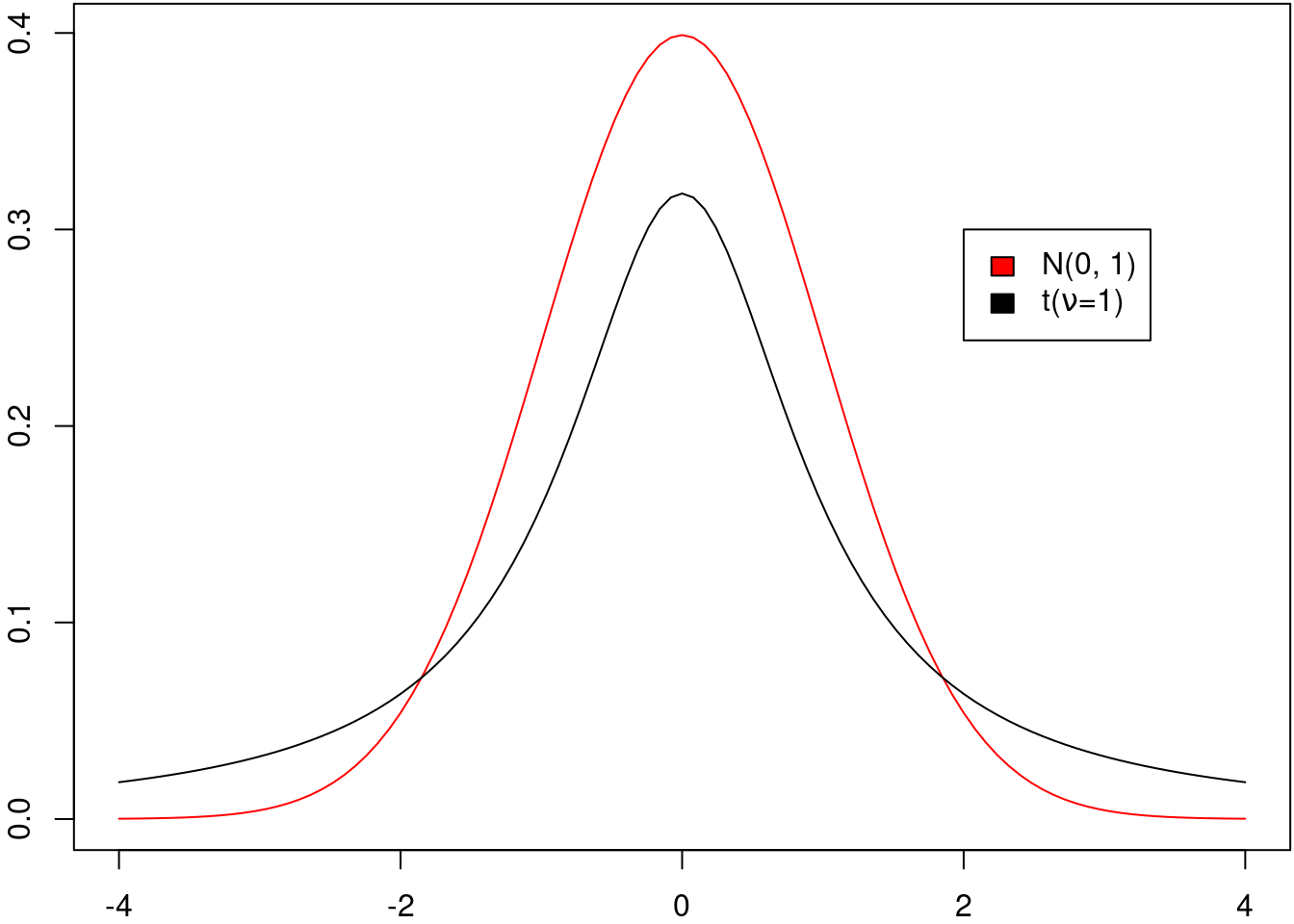
Figura 14.7: Gráficos da densidade de probabilidade para a distribuição normal padrão (vermelho) e da distribuição t de Student com 1 grau de liberdade.
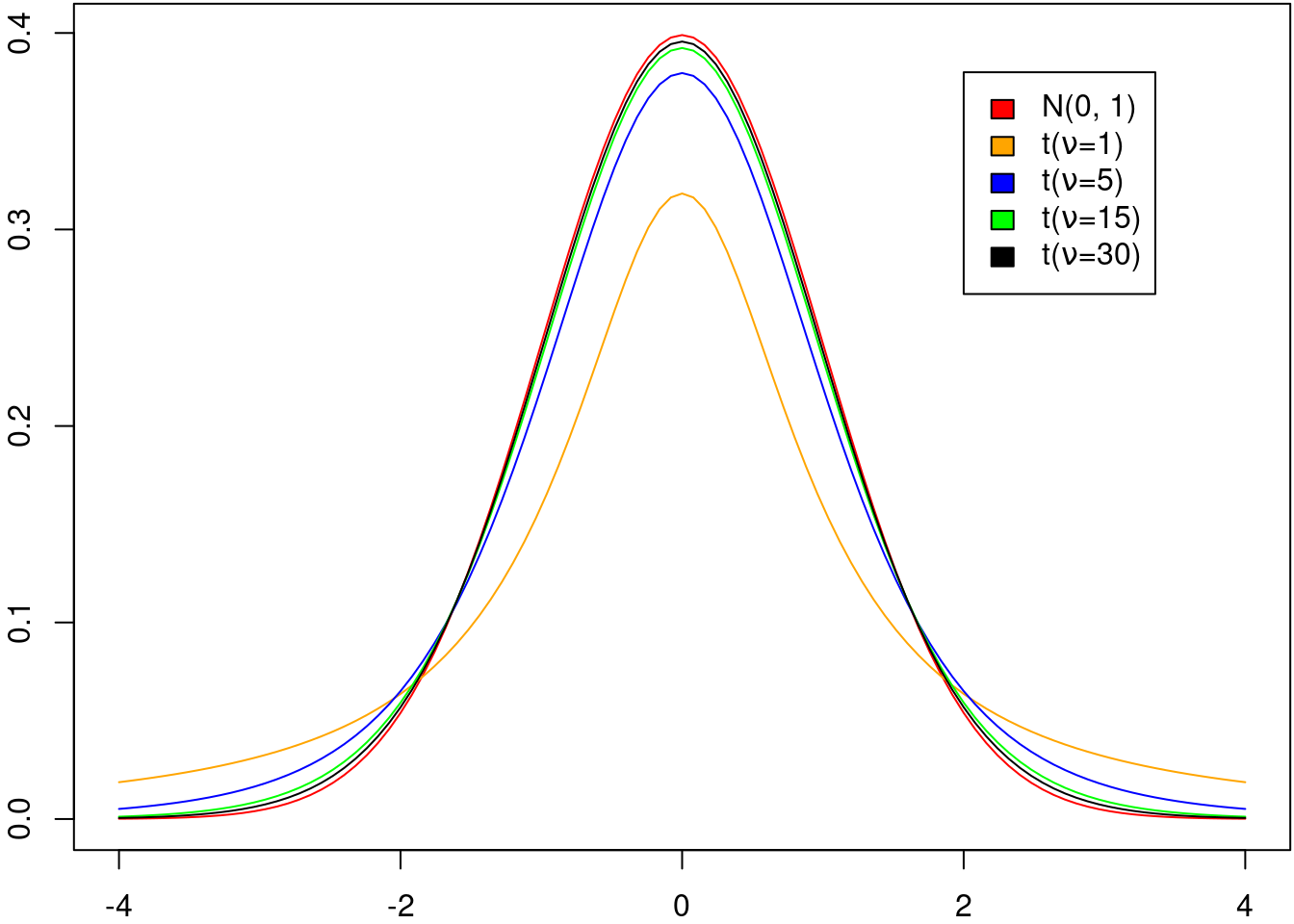
Figura 14.8: Gráficos da densidade de probabilidade para a distribuição normal padrão (vermelho) e da distribuição t de Student com graus de liberdade iguais a 1, 5, 15 e 30, respectivamente.
Para interpretarmos o conceito de graus de liberdade, vamos imaginar que obtivemos 1 amostra com n elementos x1, x2, …, xn, extraídos de maneira independente de uma mesma população. Temos, portanto, que os valores da amostra são iid, ou seja, independente e identicamente distribuídos. Para essa amostra, ao obtermos sua média, somamos os n valores e, nesse caso, dizemos que a média amostral tem n graus de liberdade, porque foi calculada usando-se os n valores independentes da amostra.
Para a variância da amostra, temos que calcular:
\(\begin{aligned} &\ s^2 =\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2 \end{aligned}\)
Observemos que, no somatório, temos agora não n valores independentes, pois a média amostral é função dos n valores da amostra. Como \(\sum_{i=1}^{n}(x_i-\bar{x})=0\), um dos termos \((x_i-\bar{x})\) é o oposto da soma dos demais. Nesse caso, perdemos um grau de liberdade e a variância amostral tem, portanto, n - 1 graus de liberdade.
É muito raro conhecermos o desvio padrão da população, portanto a construção do intervalo de confiança quase sempre envolve estimativas pontuais de \(\mu\) e \(\sigma\). Quando \(\sigma\) não é conhecido, usamos sua estimativa S para a construção do intervalo de confiança da média, ou seja, usamos \(S_{\bar{X}}=\frac{S}{\sqrt{n}}\) como estimativa do desvio padrão da média amostral. Quando o desvio padrão é estimado, devemos usar a distribuição t ao invés da distribuição normal, embora, para amostras suficientemente grandes, z possa também ser utilizado, uma vez que a distribuição t se aproxima da distribuição normal à medida que n aumenta. Os valores de t são maiores do que os obtidos com a variável normal padronizada (z), portanto o intervalo de confiança será mais largo do que quando \(\sigma\) é conhecido. A fórmula para o intervalo de confiança para a média quando estimamos \(\sigma\) por S é dada pela expressão (14.6), substituindo-se \(z_{1-\alpha/2}\) por \(t_{n-1, 1-\alpha/2}\) e \(\sigma\) por S:
\[\begin{align} \left[\bar{X} - t_{n-1, 1-\alpha/2} \frac{S}{\sqrt{n}}, \bar{X} + t_{n-1, 1-\alpha/2}\frac{S}{\sqrt{n}}\right] \tag{14.9} \end{align}\]
o valor de \(t_{n-1, 1-\alpha/2}\) pode ser obtido no R pela expressão \(qt(1-\alpha/2, n-1)\).
No exemplo 1, vamos supor que o desvio padrão 16 tenha sido estimado a partir da amostra.
Então: \(\bar{x} = 92\) mg/dl, n = 36 e s = 16. Para \(\alpha = 5\%\) e n-1 = 35, \(t_{35, 0,975}\) é dado por:
## [1] 2.030108O intervalo de confiança será dado então por:
\([92 - 2,03 . 16/6, 92 + 2,03 . 16/6] = [86,6 - 97,4]\) (mg/dl)
Esse intervalo é ligeiramente maior, mas próximo, do que o intervalo dado por (14.7).
14.5 Intervalo de confiança para a variância
Para a variância, como vimos no capítulo anterior, um bom estimador não tendencioso e consistente é dado por:
\[\begin{align} S^2 =\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2 \tag{14.10} \end{align}\]
Se soubermos a distribuição de probabilidades desse estimador, então poderíamos calcular o intervalo de confiança para a variância de modo análogo ao realizado no caso da média da distribuição.
Multiplicando e dividindo o segundo membro de (14.10) por \(\sigma^2\), podemos reescrever o estimador S2 como abaixo, :
\(\begin{aligned} &\ S^2 =\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2=\frac{\sigma^2}{n-1}\sum_{i=1}^{n}\frac{(X_i-\bar{X})^2}{\sigma^2} \end{aligned}\)
Quando Xi for uma variável aleatória com distribuição normal, o somatório na expressão acima terá uma distribuição conhecida como qui ao quadrado com (n-1) graus de liberdade, sendo representada por \(\chi_{n-1}^2\):
\(\begin{aligned} &\ S^2 \sim \frac{\sigma^2}{n-1}\chi_{n-1}^2 \end{aligned}\)
\(\boldsymbol{\chi_{n,p}^2}\) significa o valor da variável aleatória \(\chi_{n}^2\) que segue a distribuição qui ao quadrado para o qual \(\boldsymbol{P(\chi_{n,p }^2 \leq \chi_{n}^2) = p}\), ou seja, a área sob a curva qui ao quadrado à esquerda de \(\boldsymbol{\chi_{n,p}^2}\) é igual a p.
Para obtermos então o intervalo com nível de confiança igual a \((1 - \alpha)\%\), a partir da distribuição acima, achamos os valores \(\chi_{n-1,\alpha/2}^2\) e \(\chi_{n-1,1-\alpha/2}^2\) para os quais o intervalo abaixo contém, com probabilidade \((1 - \alpha)\%\), a estimativa da variância em uma amostra de tamanho n:
\(\begin{aligned} &\ \frac{\sigma^2}{n-1}\chi_{n-1,\alpha/2}^2 \leq S^2 \leq \frac{\sigma^2}{n-1}\chi_{n-1,1-\alpha/2}^2 \end{aligned}\)
Isolando a variância \(\sigma^2\) na expressão acima, obtemos então o intervalo de confiança ao nível de \((1 - \alpha)\%\) para a variância da população de uma variável aleatória que segue a distribuição normal:
\[\begin{align} S^2 \frac{n-1}{\chi_{n-1,1-\alpha/2}^2} \leq \sigma^2 \leq S^2 \frac{n-1}{\chi_{n-1,\alpha/2}^2} \tag{14.11} \end{align}\]
Exemplo 2: Uma amostra de 6 cobaias é analisada para verificar a dosagem de um certo composto, obtendo-se a média amostral igual a 14,1 mg/dl e a variância igual a 2,1 (mg/dl)2. Obter intervalos de confiança, ao nível de 95%, para a média e a variância populacional, assumindo que os dados seguem uma distribuição normal.
Como temos uma amostra pequena, n = 6, para determinar o IC (intervalo de confiança), temos que usar a distribuição t de Student, com \(\alpha =(1 - 0,95) = 0,05\) e número de graus de liberdade igual a 5 (6-1).
\[\begin{align} \left[\bar{x} - t_{n-1, \alpha/2} \frac{s}{\sqrt{n}} \leq \mu \leq \bar{X} + t_{n-1, \alpha/2}\frac{s}{\sqrt{n}}\right] \end{align}\]
O valor de \(t_{n-1,\alpha/2}\), para n = 6 e \(\alpha = 0,05\) pode ser obtido no R com a função qt(0.975, df=5), sendo igual a 2,57.
## [1] 2.570582Logo, entrando com os valores na expressão (14.9), teremos que o intervalo de confiança para a média será dado por
\(14,1 - 2,57 \sqrt{\frac{2,1}{6}} \leq \mu \leq 14,1 + 2,57 \sqrt{\frac{2,1}{6}}\)
\(12,58 \leq \mu \leq 15,62 \ (mg/dl)\)
Para a variância, usamos a expressão (14.11), mas precisamos obter os valores \(\chi_{5;0,025}^2\) e \(\chi_{5;0,975}^2\). No R, as expressões qchisq(0.025, df=5) e qchisq(0.975, df=5) nos darão os valores desejados de \(\chi_{5;0,025}^2\) e \(\chi_{5;0,975}^2\).
## [1] 0.8312116## [1] 12.8325Entrando com esses e os demais valores necessários na equação (14.11), teremos o intervalo de confiança para a variância:
\(2,1 \frac{5}{12,8325} \leq \sigma^2 \leq 2,1\frac{5}{0,8312}\)
\(0,82 \leq \sigma^2 \leq 12,63\ (mg/dl)^2\)
14.6 Distribuição qui ao quadrado
Seja X uma variável aleatória com distribuição \(N(\mu, \sigma)\) e \(Z = \frac{X - \mu}{\sigma}\) a correspondente variável normal padronizada. Então a variável aleatória \(Z^2\) é uma variável aleatória não negativa e sua distribuição é denominada distribuição qui ao quadrado (\(\chi_1^2\)) com um grau de liberdade.
Agora consideremos duas variáveis normais padronizadas Z1 e Z2 independentes. Nesse caso, a soma \(Z_1^2 + Z_2^2\) a segue uma distribuição \(\chi_2^2\) com dois graus de liberdade. Analogamente, a soma de n variáveis aleatórias normais padronizadas independentes terá uma distribuição \(\chi_n^2\) com n graus de liberdade.
\(\begin{aligned} &\ \chi_n^2 = Z_1^2 + Z_2^2 + \dots + Z_n^2 \end{aligned}\)
O valor esperado e a variância de \(\chi_n^2\) são, respectivamente
\(\begin{aligned} &\ E[\chi_n^2] = n \\ \\ &\ var[\chi_n^2] = 2n \end{aligned}\)
Usa-se como representação geral da variável qui ao quadrado a expressão \(\chi_\nu^2\), onde \(\nu\) corresponde ao número de graus de liberdade. Para n > 30, temos que a distribuição qui ao quadrado se aproxima bem de uma distribuição normal com média n e variância 2n.
Apesar de não usarmos nesse texto a função matemática da distribuição qui ao quadrado, ela é dada pela expressão:
\(\begin{aligned} f(\chi_\nu^2) = \frac{1}{2^{\frac{\nu}{2}}\Gamma(\frac{\nu}{2})}(\chi_\nu^2)^{\frac{\nu}{2}-1}e^{-\frac{\chi_\nu^2}{2}},\ \chi_\nu^2 > 0 \end{aligned}\)
onde \(\Gamma(.)\) é a função gama que aparece na distribuição t de Student (equação (14.8)). \(\chi_\nu^2\) é a variável da função f(.), ou seja, ela não é uma variável elevada ao quadrado, mas sim a própria variável na expressão.
A figura 14.9 mostra gráficos da distribuição qui ao quadrado para diferentes graus de liberdade (\(\nu\) = 2, 10, 20 e 30).
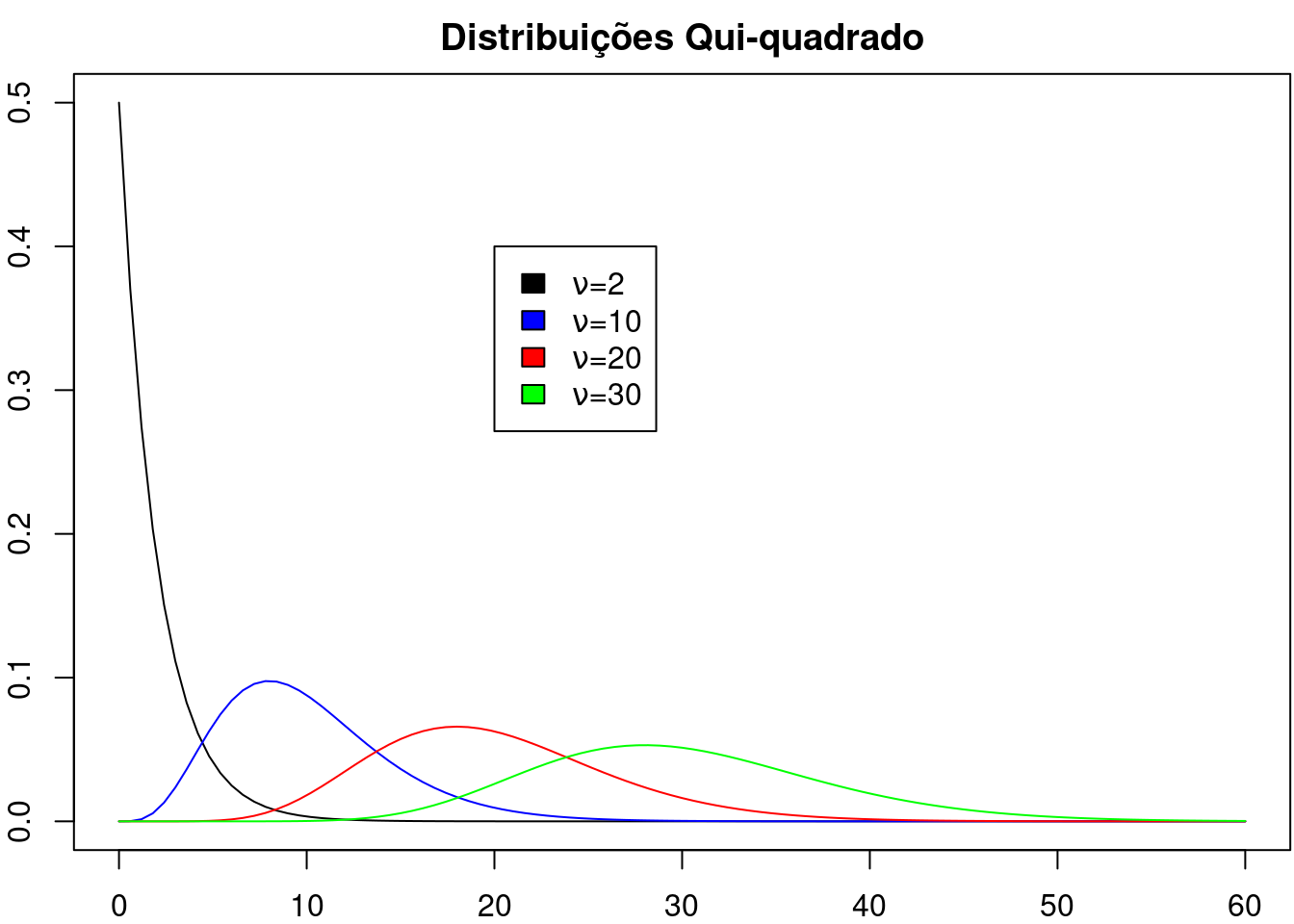
Figura 14.9: Gráficos de distribuições qui ao quadrado com graus de liberdade iguais a 2, 10, 20 e 30, respectivamente.
14.7 Intervalo de confiança para proporções
Vimos no capítulo anterior que a probabilidade p de sucesso um experimento de Bernoulli pode ser estimada pela proporção de sucessos (\(\hat{P}\)) em n experimentos de Bernoulli. Assim, sendo X o número de sucessos nos n experimentos, temos:
\[\begin{align} \hat{P} = \frac{X}{n} \tag{14.12} \end{align}\]
Para n suficientemente grande, a distribuição de \(\hat{P}\) pode ser aproximada por uma distribuição normal com média e variância dadas por:
\[\begin{align} E[\hat{P}] = \frac{E[X]}{n}=\frac{np}{n}= p \tag{14.13} \end{align}\]
\[\begin{align} &\ var[\hat{P}] = \frac{var[X]}{n^2}=\frac{np(1-p)}{n^2}= \frac{p(1-p)}{n} \tag{14.14} \end{align}\]
Se realizarmos n experimentos de Bernoulli e observarmos a proporção de sucessos, podemos então estimar o intervalo de confiança para a proporção real de sucessos p, aplicando a fórmula para o intervalo de confiança da média de uma distribuição normal (equação (14.6)), substituindo \(\mu\) por p, \(\bar{X}\) por \(\hat{P}\), e \(\sigma\) por \(\sqrt{\frac{\hat{P}(1-\hat{P})}{n}}\) . Assim o intervalo de confiança ao nível \((100-\alpha)\)% para a proporção de sucessos em n experimentos de Bernoulli para n suficientemente grande é dado por:
\[\begin{align} \hat{P} - z_{1-\alpha/2} \sqrt{\frac{\hat{P}(1-\hat{P})}{n}} \leq p \leq \hat{P} + z_{1-\alpha/2} \sqrt{\frac{\hat{P}(1-\hat{P})}{n}} \tag{14.15} \end{align}\]
Exemplo 3: vamos considerar que desejamos estimar a proporção de aparelhos de raios-X que estejam com defeito e produzam um excesso de radiação. Tomando-se uma amostra de 40 aparelhos, identificou-se que 12 estavam com defeito. O nosso problema aqui é determinar um intervalo de confiança para a proporção populacional p de aparelhos que possam estar com defeito. Na terminologia utilizada neste texto, o sucesso, nesse caso, é considerado um aparelho com defeito.
A partir da amostra, obtemos \(\hat{p} = 12/40 = 0,30\). Para um intervalo de confiança de 95%, obtemos \(z_{1-\alpha/2}\) = 1,96. Com esses valores, obtemos o IC (intervalo de confiança):
\(0,3 - 1,96 \sqrt{\frac{0,3(1-0,3)}{40}} \leq p \leq 0,3 + 1,96 \sqrt{\frac{0,3(1-0,3)}{40}}\)
\(0,16 \leq p \leq 0,44\)
Nesse caso, estamos assumindo uma aproximação para a normal. Um resultado mais acurado pode ser obtido, introduzindo-se a correção de continuidade, somando 0,5/n para o limite superior e subtraindo esse valor do limite inferior, obtendo os valores 0,1475 e 0,4525 para os limites inferior e superior, respectivamente. Assim, com 95% de confiança, entre 14,75% e 45,25% dos equipamentos de raios x apresentam o defeito.
14.8 Resumo para obtenção de intervalos de confiança de um parâmetro
Resumindo o que vimos até aqui, podemos generalizar os passos para obter um intervalo de confiança de um determinado parâmetro. Basicamente são quatro passos, que serão ilustrados com os casos discutidos nas seções precedentes.
1) Encontrar um estimador para o parâmetro
Exemplos:
- Para a média de uma distribuição de uma variável aleatória X:
\[\begin{align} &\ \bar{X} =\frac{1}{n}\sum_{i=1}^{n}X_i \end{align}\]
- Para a variância de uma distribuição:
\[\begin{align} &\ S^2 =\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2 \end{align}\]
- para a probabilidade de sucesso em uma distribuição binomial:
\[\begin{align} &\ \hat{P} =\frac{\text{contagem de ocorrências do evento}}{\text{número de experimentos}} \end{align}\]
2) Encontrar a distribuição do estimador do parâmetro de interesse
- Para a média de uma distribuição normal com variância conhecida \(\sigma\):
\[\ Z =\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\]
onde Z segue a distribuição normal padrão.
- Para a média de uma distribuição normal com variância desconhecida:
\[\ T =\frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}}\]
onde T segue a distribuição t de Student com n-1 graus de liberdade
- Para a variância de uma distribuição normal com média desconhecida:
\[\ S^2 =\frac{\sigma^2}{n-1}\chi_{n-1}^2\]
onde \(\chi_{n-1}^2\) segue a distribuição qui ao quadrado com n-1 graus de liberdade.
- para a probabilidade de sucesso em uma distribuição binomial, com n suficientemente grande:
\[\ Z =\frac{\hat{P}-p}{\sqrt{\frac{\hat{P}(1-\hat{P})}{n}}}\]
onde Z segue a distribuição normal padrão
3) Especificar o nível de confiança \(\boldsymbol{(1 - \alpha)}\) e determinar o intervalo que contém, com probabilidade \(\boldsymbol{(1 - \alpha)}\), a estimativa do parâmetro
- Para a média de uma distribuição normal com variância conhecida \(\sigma\):
\[\begin{align} &\ \mu - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \bar{X} \leq \mu + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{align}\]
- Para a média de uma distribuição normal com variância desconhecida:
\[\begin{align} &\ \mu - t_{n-1,1-\alpha/2} \frac{S}{\sqrt{n}} \leq \bar{X} \leq \mu + t_{n-1, 1-\alpha/2}\frac{S}{\sqrt{n}} \end{align}\]
- Para a variância de uma distribuição normal com média desconhecida:
\[\begin{align} &\ \frac{\sigma^2}{n-1}\chi_{n-1,\alpha/2}^2 \leq S^2 \leq \frac{\sigma^2}{n-1}\chi_{n-1,1-\alpha/2}^2 \end{align}\]
- para a probabilidade de sucesso em uma distribuição binomial, com n suficientemente grande:
\[\begin{align} &\ p - z_{1-\alpha/2} \sqrt{\frac{\hat{P}(1-\hat{P})}{n}} \leq \hat{P} \leq p + z_{1-\alpha/2} \sqrt{\frac{\hat{P}(1-\hat{P})}{n}} \end{align}\]
4) Nas expressões em 3, inverter as relações para obter o intervalo de confiança
- Para a média de uma distribuição normal com variância conhecida \(\sigma\):
\[\begin{align} &\ \bar{X} - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{align}\]
- Para a média de uma distribuição normal com variância desconhecida:
\[\begin{align} &\ \bar{X} - t_{n-1,1-\alpha/2} \frac{S}{\sqrt{n}} \leq \mu \leq \bar{X} + t_{n-1, 1-\alpha/2}\frac{S}{\sqrt{n}} \end{align}\]
- Para a variância de uma distribuição normal com média desconhecida:
\[\begin{align} &\ S^2 \frac{n-1}{\chi_{n-1,1-\alpha/2}^2} \leq \sigma^2 \leq S^2 \frac{n-1}{\chi_{n-1,\alpha/2}^2} \end{align}\]
- para a probabilidade de sucesso em uma distribuição binomial, com n suficientemente grande:
\[\begin{align} &\ \hat{P} - z_{1-\alpha/2}\sqrt{\frac{\hat{P}(1-\hat{P})}{n}} \leq p \leq \hat{P} + z_{1-\alpha/2} \sqrt{\frac{\hat{P}(1-\hat{P})}{n}} \end{align}\]
Portanto, para qualquer parâmetro que estimamos usando uma estatística, não somente os exemplificados acima, podemos determinar o intervalo de confiança se conhecermos a distribuição amostral da estatística de interesse.
14.9 Exercícios
As idades de uma amostra aleatória de 50 membros de uma certa sociedade acadêmica são obtidas e encontra-se que \(\bar{x} = 53,8\) anos e \(s = 9,89\) anos. A idade dessa população segue uma distribuição normal, mas não conhecemos nem a média nem a variância.
- Calcule o intervalo com 90% de confiança para a média de idade de todos os membros da sociedade.
- Se a média acima tivesse sido obtida de uma amostra aleatória de 100 indivíduos da população, qual seria o intervalo com 90% de confiança para a média da população?
- Calcule o intervalo com 99% de confiança para a variância da idade de todos os membros da sociedade.
- Quais são os passos para construir o intervalo de confiança para a média amostral de uma população que segue a distribuição normal e você não sabe qual é a variância populacional?