19 Regressão linear

19.1 Introdução

Os conteúdos desta seção e das seções 19.2 e 19.3 podem ser visualizados neste vídeo.

A figura 19.1 mostra um diagrama de dispersão relacionando as variáveis prestígio (prestige) e nível educacional (education). Essas variáveis constam do conjunto de dados Prestige, disponível no pacote carData (GPL-2 | GPL-3). Esse arquivo contém dados sobre a renda, a escolaridade, o prestígio, etc., relativos a 102 ocupações no Canadá. A variável prestige é o escore de prestígio de uma ocupação de acordo com o método de Pineo-Porter. O nível educacional foi medido em anos de escolaridade.

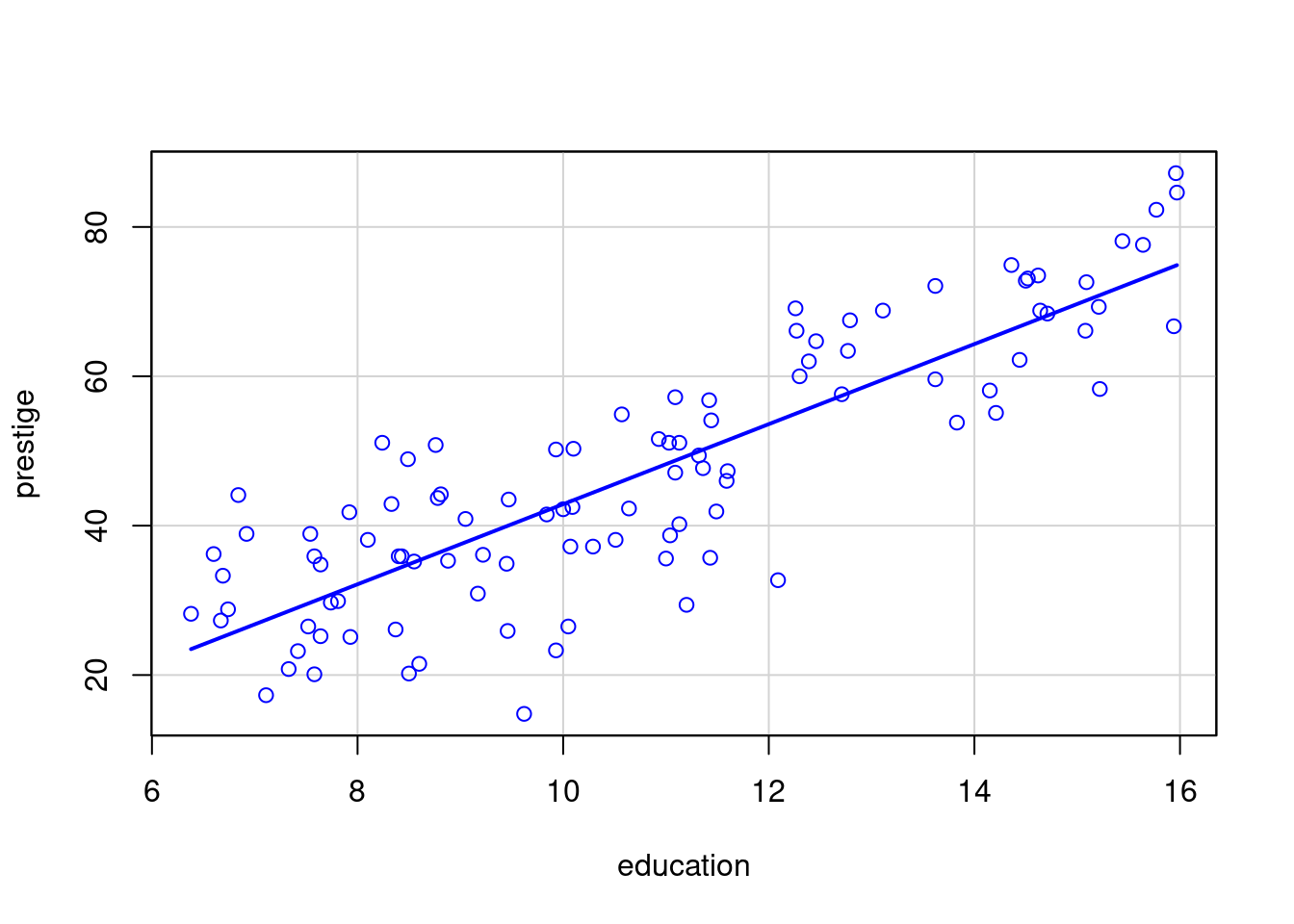
Figura 19.1: Diagrama de dispersão das variáveis prestige e education.

Cada ponto no gráfico corresponde aos valores do nível educacional (abscissa) e do escore do prestígio (ordenada) para cada ocupação. Observando o gráfico, podemos verificar que há uma tendência de valores maiores do nível educacional estarem associados a valores maiores de prestígio, e que essa relação é aproximadamente linear, indicada pela reta azul. Essa reta é chamada reta de regressão.

Como outro exemplo, a figura 19.2 mostra um diagrama de dispersão da fração de ejeção do ventrídulo esquerdo em função da relação neutrófilo-linfócito, obtido no estudo de Durmus et al. (Durmus et al. 2015). Cada ponto no gráfico corresponde aos valores da relação neutrófilo-linfócito (abscissa) e da fração de ejeção (ordenada) para cada paciente do estudo. Esse gráfico sugere que a fração de ejeção do ventrídulo esquerdo tende a diminuir quando a relação neutrófio-linfócito aumenta. Os autores apresentaram no gráfico a reta que melhor se ajusta a esses dados.

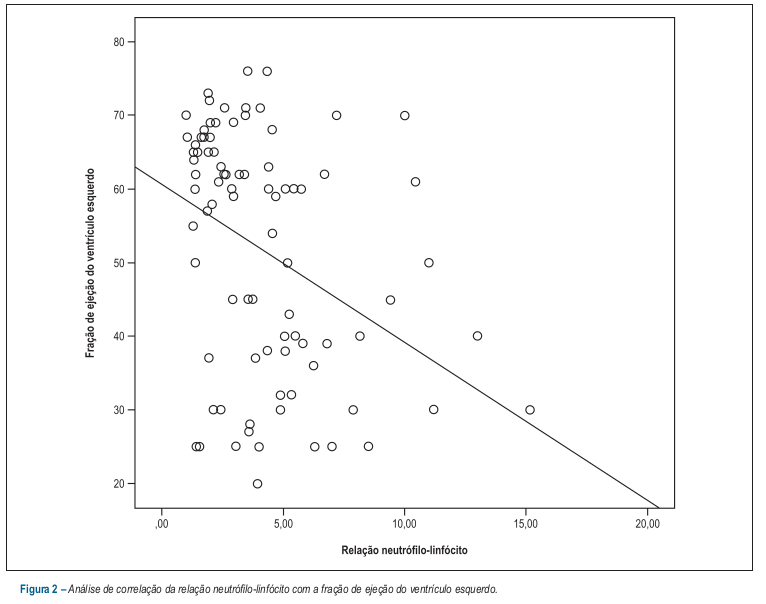
Figura 19.2: Diagrama de dispersão com a reta de regressão da fração de ejeção do ventrídulo esquerdo em função da relação neutrófilo-linfócito. Fonte: (Durmus et al. 2015) (CC BY).

Este capítulo irá apresentar a análise de regressão simples, a qual permite a identificação dos coeficientes da reta que melhor se ajusta aos dados, e mostrar como calcular intervalos de confiança desses coeficientes e realizar predições. Também serão apresentadas técnicas que permitem identificar quando um modelo de regressão é válido. A análise de regressão deve esse nome ao fato de que um dos pioneiros da área, Galton, observou que filhos de pais altos tendiam a ser mais baixos do que os pais e filhos de pais baixos tendiam a ser mais altos que eles, sugerindo que a altura dos filhos tendia a regredir aos valores da altura média da população, daí o nome reta de regressão à relação entre a altura dos pais e dos filhos e de regressão linear a essa técnica estatística.

19.2 Equação da reta

A  figura  19.3   apresenta   uma   reta   no  plano  XY,   passando   por  dois   pontos  \(P_1(X_0, Y_0)\)   e \(P_2(X_0+\Delta X, Y_0+\Delta Y)\).

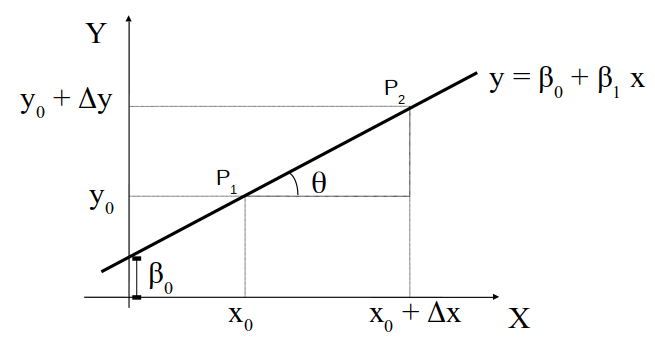
Figura 19.3: Gráfico e equação da reta.

Uma reta é dada pela expressão:

\(\ y = \beta_1 x + \beta_0\),

onde \(\beta_1\) é a inclinação da reta e \(\beta_0\) é a interseção da reta com o eixo y. \(\beta_1\) e \(\beta_0\) são os coeficientes da reta. O valor de \(\beta_1\) é dado pela expressão:

\[\begin{align} \beta_1 = \frac{(Y_0+\Delta Y - Y_0)}{(X_0+\Delta X - X_0)} = \frac{\Delta Y}{\Delta X} \tag{19.1} \end{align}\]

e indica o quanto os valores de y variam para cada unidade de aumento na variável x.

19.3 Método dos mínimos quadrados

Quando a relação entre duas variáveis numéricas pode ser aproximada por uma linha reta, como na figura 19.1, então devem ser encontrados os coeficientes da reta que melhor expresse essa relação linear. Como obter esses coeficientes? Observem a figura 19.4.

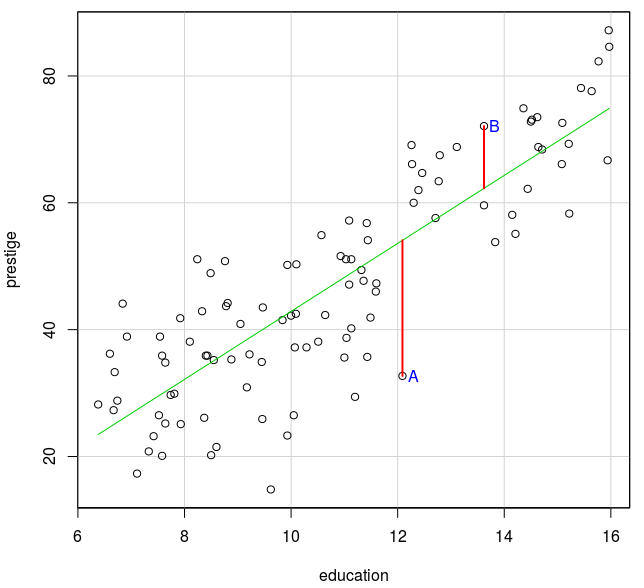
Figura 19.4: Distância vertical entre cada ponto do conjunto de dados à reta de regressão.

A reta que melhor se ajusta aos dados na figura 19.4 deve ser aquela que minimiza a distância vertical entre cada ponto e a reta, mas não basta minimizar a distância vertical de um único ponto, é preciso levar em conta todos os pontos. A figura 19.4 mostra dois pontos A e B e os segmentos que unem esses pontos à reta de regressão e que indicam a distância vertical de cada ponto à reta. Vamos chamar de X a variável education e de Y a variável prestige, e n o número de pontos no conjunto de dados (n = 102 no conjunto de dados Prestige).

Vamos considerar que a reta de regressão é dada pela expressão:

\[\begin{align} Y = \beta_1 X + \beta_0 \tag{19.2} \end{align}\]

Vamos chamar de \(\hat{y_i}\) o valor de y na reta de regressão correspondente ao ponto x_i. Vamos definir a distância vertical do ponto (x_i, y_i) (i = 1,…, n) à reta de regressão como o valor absoluto da diferença entre o valor y_i e o valor \(\hat{y}_i\) do ponto na reta correspondente a x_i:

| \(y_i - \hat{y}_i\) |, onde \(\hat{y}_i = \beta_0 + \beta_1 x_i\)

O método mais usado para determinar os coeficientes da reta de regressão é calcular esses coeficientes de tal modo que a soma do quadrado das distâncias de cada ponto à reta de regressão seja mínima, ou seja, calcular os coeficientes b₀ e b₁ de tal modo que a expressão abaixo seja mínima:

\[\begin{align} \sum_{i=1}^{n} (y{_i} - \hat{y}_i)^2 = \sum_{i=1}^{n} [y{_i} - (b_0 + b_1 x{_i})]^2 \tag{19.3} \end{align}\]

Por procurar minimizar o quadrado das distâncias, esse método é conhecido como método dos mínimos quadrados. A aplicação Determinação dos coeficientes da reta de regressão ilustra essa ideia. A figura 19.5 mostra a página inicial dessa aplicação.

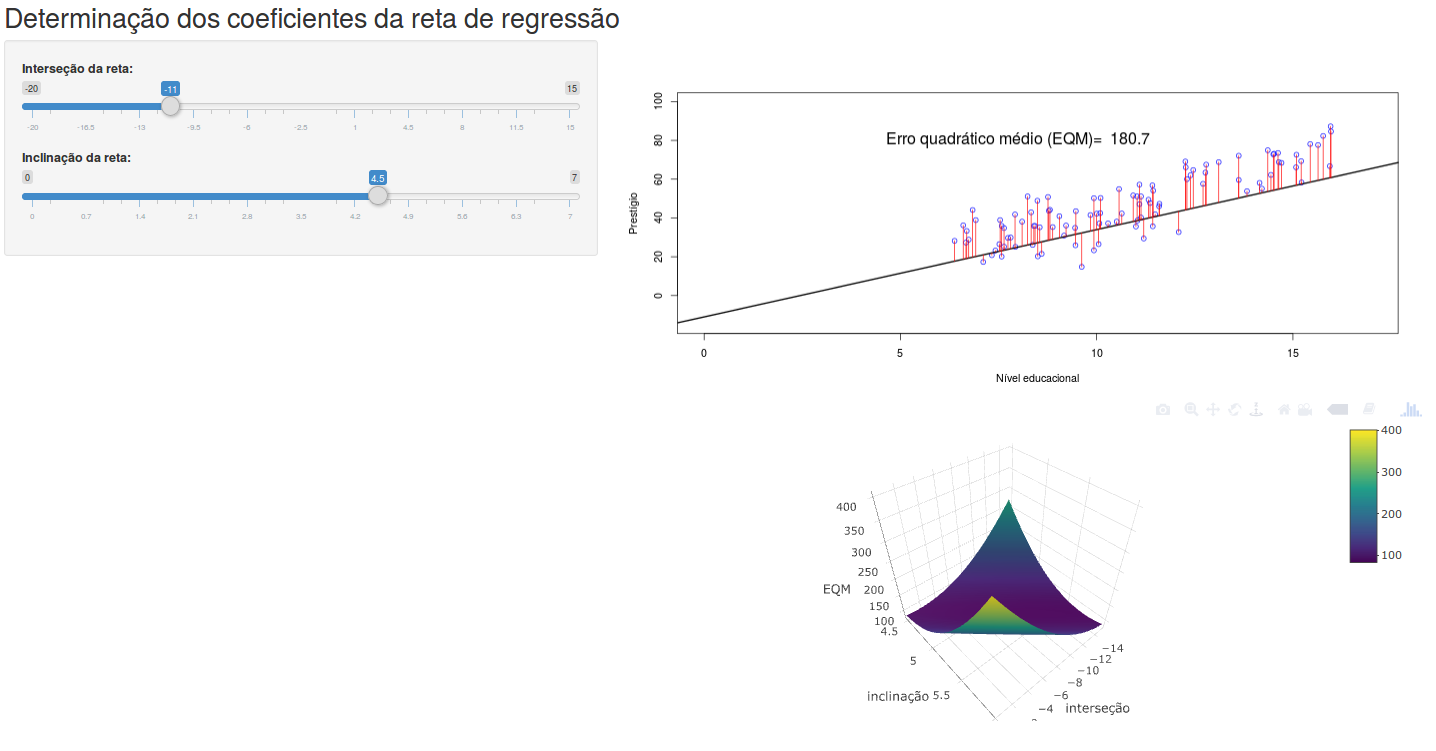
Figura 19.5: Aplicação que ilustra o princípio do método dos mínimos quadrados.

No painel à esquerda, o usuário pode variar a inclinação (coeficiente b₁) e a interseção da reta (coeficiente b₀), a qual é exibida no gráfico superior do painel principal, juntamente com as distâncias verticais de cada ponto à reta. À medida que o usuário alterar os coeficientes da reta, o gráfico mostra a nova reta e o valor do erro quadrático médio que é a expressão (19.3) dividida pelo número de pontos - 2. Minimizar o erro quadrático médio é equivalente a minimizar a expressão (19.3). Se o usuário alterar os valores da interseção e inclinação da reta, verá que o valor do erro quadrático médio vai variando. Ao escolher valores da interseção próximos a -10,732 e valores da inclinação próximos a 5,361, os valores do erro quadrático médio são próximos ao mínimo valor do erro quadrático médio. O mesmo pode ser observado no gráfico da parte inferior do painel principal (figura 19.6).

O gráfico da figura 19.6 mostra uma superfície que representa o valor do erro quadrático médio (EQM) para cada combinação de valores dos coeficientes \(b_0\) (interseção) e \(b_1\) (inclinação) da reta de regressão. Ao clicarmos com o mouse sobre a superfície, o gráfico mostra os correspondentes valores de \(b_0\), \(b_1\) e do EQM. Ao movermos o mouse, os pontos sobre a superfície vão se alterando. Ao pressionarmos e arrastarmos o mouse, podemos girar o gráfico em torno dos eixos coordenados. Ao escolhermos certo ângulo de visualização do gráfico e ao movermos o mouse, podemos observar os valores de b₀ e b₁ correspondentes aos menores valores do EQM. Diversos ícones na parte superior direita do gráfico permitem a realização de diversas operações como zoom, baixar a imagem no formato png, mover o gráfico, etc.

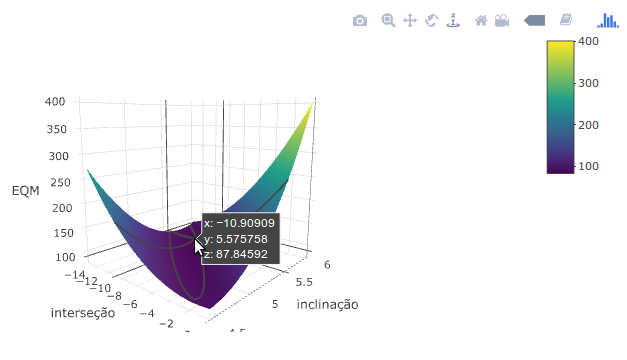
Figura 19.6: Erro quadrático médio em função dos valores dos coeficientes b₀ (interseção) e b₁ (inclinação) da reta de regressão.

Matematicamente existem expressões obtidas a partir das derivadas da função do erro quadrático (19.3) que permitem a obtenção dos valores de \(b_0\) e \(b_1\) que minimizam o erro quadrático, sem a necessidade de usarmos o método de tentativa e erro. Essas expressões são dadas por (Costa Neto 1977):

\[\begin{align} b_1 &= \frac{\sum_{i=1}^{n} (x{_i} - \bar{x}) {y}_i} {\sum_{i=1}^{n} (x{_i} - \bar{x})^2} \tag{19.4} \end{align}\]

\[\begin{align} b_0 &= \bar{y} - b_1 \bar{x} \tag{19.5} \end{align}\]

19.4 Modelo de regressão linear

O conteúdo desta seção pode ser visualizado neste vídeo.

O modelo de regressão linear simples pode ser escrito como:

\[\begin{align} Y_i = \beta_0 + \beta_1 X_i + \epsilon_i \tag{19.6} \end{align}\]

onde:

i - indica cada um dos pares de valores (x_i, y_i) (i = 1, 2, …, n);

X_i – i-ésimo valor da variável independente X;

\(\beta_0\) – corresponde à interseção da reta de regressão com o eixo Y;

\(\beta_1\) – inclinação da reta de regressão;

\(\epsilon_i\) – desvio do valor observado Y_i em relação ao valor previsto pela reta de regressão no ponto X_i. Os erros \(\epsilon_i\) supostamente seguem uma distribuição normal com média 0 e variância \(\sigma^2\).

Os coeficientes \(\beta_0\) e \(\beta_1\) da reta de regressão podem ser estimados por meio do método dos mínimos quadrados e as estimativas serão representadas como b₀ e b₁, respectivamente. Então os valores estimados de Y para cada valor da variável X serão dados por:

\(\begin{aligned} \hat{y}_i = b_0 + b_1 x_i \end{aligned}\)

A partir do modelo de regressão, podemos:

1. realizar um teste de hipótese de que a inclinação da reta de regressão é nula, ou seja, não existe uma relação linear entre as variáveis X e Y;

2. estimar os intervalos de confiança para os parâmetros \(\beta_0\) e \(\beta_1\) da reta de regressão;

3. verificar a validade do modelo de regressão;

4. estimar o intervalo de confiança para o valor esperado de Y para um dado valor de X;

5. estimar o intervalo de confiança para o valor de Y para um dado valor de X.

As 3 primeiras questões serão tratadas a seguir.

19.4.1 Teste de hipótese

Para verificar se não existe uma relação linear entre as variáveis X e Y em um modelo de regressão linear, o seguinte teste de hipótese pode ser realizado:

H₀: \(\beta_1 = 0\)

H₁: \(\beta_1 \neq 0\)

Para verificar a hipótese H₀, um raciocínio semelhante ao realizado para a análise de variância para um fator (capítulo 18) pode ser empregado, particionando a soma dos quadrados da variável Y em relação à média geral de Y.

A média aritmética de todos os valores de Y (média geral) é dada por:

\[\begin{align} \bar{Y} = \frac{\sum_{i=1}^{n} Y_{i}}{n} \tag{19.7} \end{align}\]

A média aritmética de todos os valores de X é dada por:

\[\begin{align} \bar{X} = \frac{\sum_{i=1}^{n} X_{i}}{n} \tag{19.8} \end{align}\]

Partição da soma dos resíduos em relação à média geral

A expressão a seguir mostra que o desvio de cada valor da variável aleatória Y (\(Y_i\)) em relação à média geral de Y (\(\bar{Y}\)) é igual ao desvio de Y em relação ao valor previsto pela reta de regressão (\(\hat{Y_i}\)) somado ao desvio do valor previsto pela reta de regressão em relação à média geral :

\(\underbrace{Y_{i} - \bar{Y}}_\text{desvio em relação à média geral} = \underbrace{(Y_{i} - \hat{Y_i})}_\text{desvio em relação à reta de regressão} + \underbrace{(\hat{Y_i} - \bar{Y})}_\text{desvio da reta de regressão em relação à média geral}\)

A figura 19.7 ilustra essa fatoração. Os três gráficos mostram o desvio de cada valor da variável Y em relação ao valor previsto pela reta de regressão (gráfico superior à esquerda), o desvio de cada valor previsto pela reta de regressão em relação à média geral de Y (gráfico superior à direita) e o desvio de cada valor de Y em relação à média geral de Y (gráfico inferior à esquerda).

Elevando cada desvio ao quadrado e somando os quadrados de todos os desvios, pode-se mostrar que o resultado é a expressão abaixo:

\[\begin{align} \sum_{i=1}^{n}(Y_{i} - \bar{Y})^2 = \sum_{i=1}^{n}(\hat{Y_i} - \bar{Y})^2 + \sum_{i=1}^{n}(Y_{i} - \hat{Y_i})^2 \tag{19.9} \end{align}\]

Essa expressão pode ser escrita como:

  \(SQTot = SQR + SQE\)

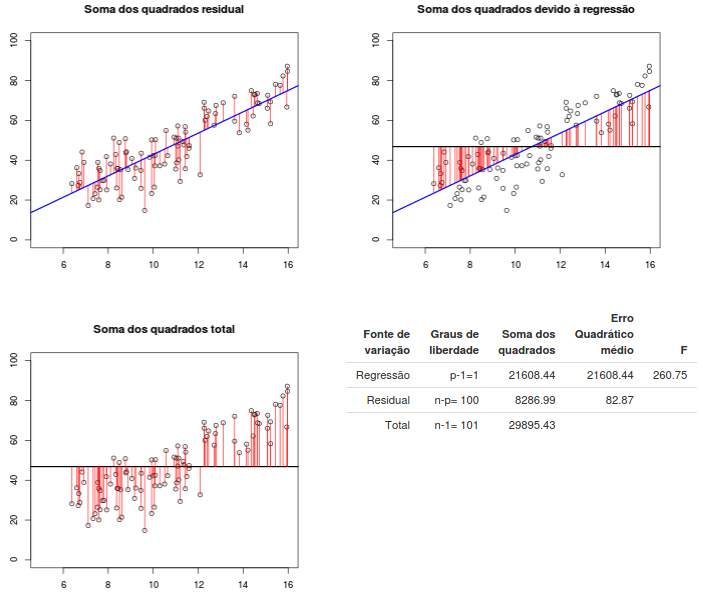
Figura 19.7: Análise de variância aplicada ao modelo de regressão linear. p = 2 no modelo (19.6).

onde:

\[\begin{align} \text{SQTot = Soma total dos quadrados} = \sum_{i=1}^{n}(Y_{i} - \bar{Y})^2 \tag{19.10} \end{align}\]

com n-1 graus de liberdade. Essa soma é mostrada na terceira linha da tabela da figura 19.7.

\[\begin{align} \text{SQE = Soma dos quadrados dos erros =} \sum_{i=1}^{n}(Y_{i} - \hat{Y_i})^2 \tag{19.11} \end{align}\]

com n-2 graus de liberdade. Essa soma é mostrada na segunda linha da tabela da figura 19.7.

\[\begin{align} \text{SQR = Soma dos quadrados devido à regressão =} \sum_{i=1}^{n}(\hat{Y_i} - \bar{Y})^2 \tag{19.12} \end{align}\]

com 1 grau de liberdade. Essa soma é mostrada na primeira linha da tabela da figura 19.7.

O erro quadrático médio (EQM) é obtido dividindo-se SQE pelo correspondente número de graus de liberdade (segunda linha da tabela da figura 19.7):

\[\begin{align} EQM = \frac{\sum_{i=1}^{n}(Y_{i} - \hat{Y_i})^2}{n - 2} \tag{19.13} \end{align}\]

O erro quadrático médio da regressão (EQMR) é obtido dividindo-se SQR pelo correspondente grau de liberdade (primeira linha da tabela da figura 19.7):

\[\begin{align} EQMR = \frac{\sum_{i=1}^{n}(\hat{Y_{i}} - \bar{Y})^2}{1} \tag{19.14} \end{align}\]

Pode-se mostrar que o valor esperado do erro quadrático médio é igual à variância do erro no modelo de regressão:

\[\begin{align} E[EQM] = \sigma^2 \tag{19.15} \end{align}\]

e que o valor esperado do erro quadrático médio da regressão é igual à expressão abaixo:

\[\begin{align} E[EQMR] = \sigma^2 + \beta_1^2\ \sum_{i=1}^{n}(X_{i} - \bar{X})^2 \tag{19.16} \end{align}\]

Teste F

Quando a hipótese nula é verdadeira, tanto o erro quadrático médio quanto o erro quadrático médio da regressão são estimadores não tendenciosos da variância do erro do modelo de regressão. Quando a hipótese nula não é verdadeira, o valor esperado do erro quadrático médio da regressão é maior do que a variância do erro, aumentando à medida que o valor absoluto da inclinação da reta de regressão aumenta.

Assim a divisão do valor do erro quadrático médio da regressão (EQMR) pelo erro quadrático médio (EQM) dá uma indicação de quanto a hipótese nula é compatível com os dados. Vamos representar o valor dessa divisão por F*:

\[\begin{align} F^* = \frac{EQMR}{EQM} \tag{19.17} \end{align}\]

Pode-se mostrar que a razão EQMR/EQM, se a hipótese nula for verdadeira, segue a distribuição F(1, n-2). Dado um nível de significância \(\alpha\), quando o valor de F*, obtido da expressão (19.17), for maior que o quantil \(1-\alpha\) da distribuição F(1, n-2), então a hipótese nula é rejeitada.

19.4.2 Intervalos de confiança para os coeficientes de regressão

Os conteúdos desta seção e da seção 19.4.3 podem ser visualizados neste vídeo.

Vamos supor que uma amostra contendo n pares de valores (x, y) sejam extraídas de uma população. Podemos imaginar duas situações distintas:

1. X e Y possuem uma distribuição conjunta normal e n unidades de observação sejam extraídas aleatoriamente de uma população e os valores de X e Y para cada unidade são medidos;

2. n valores fixos de X são estabelecidos a priori e, para cada valor de X, uma unidade de observação é extraída aleatoriamente da população de indivíduos com esse valor de X e o correspondente valor de Y é medido.

Em ambos os casos, vamos supor que a relação entre X e Y possa ser escrita da seguinte forma:

\[\begin{align} \ Y_i = \beta_0 + \beta_1 X_i +\epsilon_i,\ \ \ \ \text{i = 1, 2, ..., n}\ \ \ \ e\ \ \ \ \epsilon_i \sim N(0, \sigma^2) \tag{19.18} \end{align}\]

Como estamos lidando com amostras extraídas de uma população, é de se esperar que, se ajustarmos uma reta de regressão a cada amostra obtida, as estimativas dos coeficientes da reta de regressão irão variar de amostra para amostra.

A aplicação Variabilidade dos coeficientes da reta de regressão mostra a variabilidade das estimativas dos coeficientes de regressão (figura 19.8). Para isso, partindo de uma relação linear entre as variáveis Y e X, dada pela equação (19.18), onde \(\beta_0 = 1\), \(\beta_1 = 2\) e \(\sigma^2 = 15\), obtemos sucessivas amostras de 21 pares (x, y) onde x = 10, 11, 12, …, 30 e os valores de y são obtidos a partir da equação (19.18). Os valores de X são fixos, mas os valores de Y correspondentes a cada valor de X irão variar de amostra para amostra, devido ao componente aleatório \(\epsilon_i\).

A aplicação mostra inicialmente duas simulações (ou duas amostras de 21 pares (x, y)). Para cada amostra, uma reta de regressão é ajustada aos dados pelo método dos mínimos quadrados (mostrada no painel inferior à direita), gerando as estimativas \(b_1\) e \(b_0\) de \(\beta_1\) e \(\beta_0\), dadas pela expressões (19.4) e (19.5), respectivamente. É possível observar que as duas retas de regressão correspondentes às duas simulações são diferentes (mostradas no painel superior à direita).

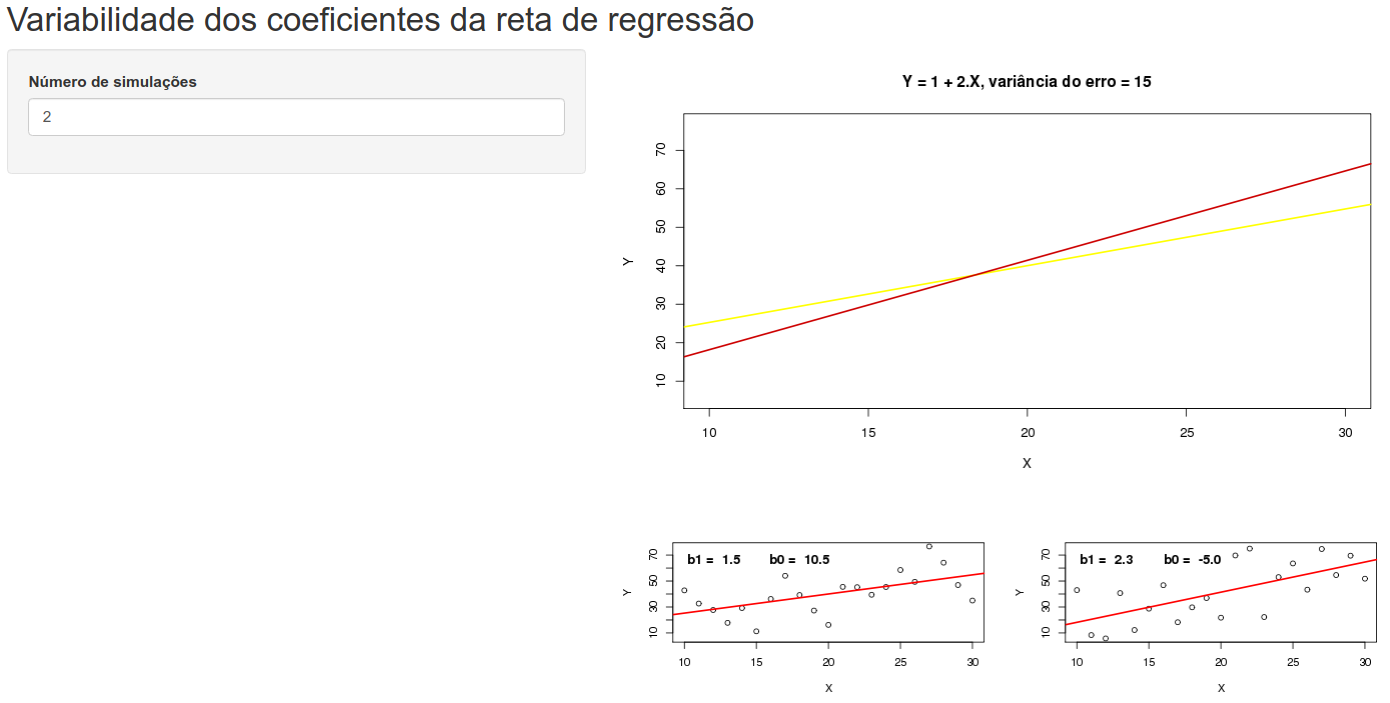
Figura 19.8: Aplicação para ilustrar a variabilidade dos coeficientes da reta de regressão. A parte superior mostra as retas de regressão correspondentes a cada simulação. Na parte inferior, são mostradas as retas de regressão correspondentes às primeiras simulações (máximo de 4). O usuário seleciona o número de simulações, até um máximo de 1000.

Aumentando o número de simulações, iremos obter um perfil das retas de regressão como mostra a figura 19.9. É possível observar uma variabilidade das estimativas dos coeficientes da reta de regressão e uma maior variação dos valores esperados de Y à medida que nos afastamos do valor médio de X.

Nas seções seguintes, serão apresentados os intervalos de confiança para os coeficientes da reta de regressão.

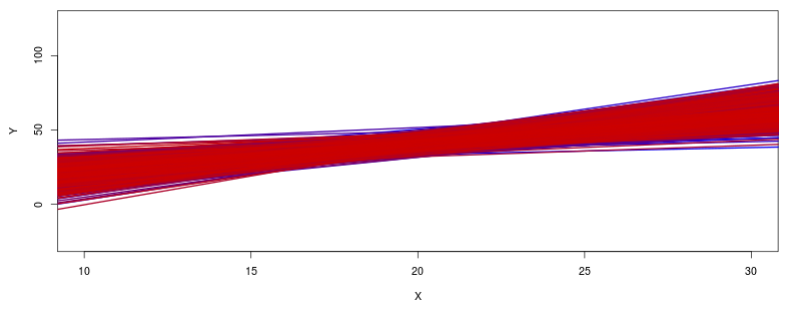
Figura 19.9: Realizando 1000 simulações na aplicação da figura 19.8. É possível observar uma maior variação dos valores esperados de Y à medida que nos afastamos do valor médio de X.

19.4.2.1 Intervalo de confiança para a inclinação da reta de regressão

É possível demonstrar (Kutner et al. 2005) que o valor esperado e a variância da estimativa da inclinação da reta de regressão pelo método dos mínimos quadrados são dados por:

  \(E[b_1] = \beta_1\)

\(\begin{aligned} &\ var[b_1] = \frac{\sigma^2} {\sum_{i=1}^{n}(X_{i} - \bar{X})^2} \end{aligned}\)

A variância \(\sigma^2\) pode ser estimada pelo EQM (equação (19.13)), de modo que a variância de \(b_1\) pode ser estimada por:

\(\begin{aligned} &\ s^2[b_1] = \frac{EQM} {\sum_{i=1}^{n}(X_{i} - \bar{X})^2} \end{aligned}\)

A estatística \(\frac{b_1 - \beta_1}{s[b_1]}\) segue uma distribuição t de Student, com n-2 graus de liberdade, de modo que o intervalo de confiança de \(\beta_1\) com nível de confiança \(1 - \alpha\) pode ser calculado a partir da expressão abaixo:

\(\begin{aligned} &\ P\left[ -t_{n-2, 1-\alpha/2} \leq \frac{b_1 - \beta_1}{s[b_1]} \leq t_{n-2, 1-\alpha/2}\right] = 1 - \alpha \end{aligned}\)

Portanto o intervalo de confiança de \(\beta_1\) com nível de confiança \(1 - \alpha\) é dado por:

\(\begin{aligned} &\ \boldsymbol{b_1 -t_{n-2, 1-\alpha/2}\ s[b_1] \leq \beta_1 \leq b_1 + t_{n-2, 1-\alpha/2} \ s[b_1]} \end{aligned}\)

19.4.2.2 Intervalo de confiança para a interseção da reta de regressão com o eixo Y

O valor esperado e a variância da estimativa da interseção da reta de regressão com o eixo Y pelo método dos mínimos quadrados são dados por:

  \(E[b_0] = \beta_0\)

e

\(\begin{aligned} &\ var[b_0] = \sigma^2 \left[\frac{1}{n}+\frac{\bar{X}^2} {\sum_{i=1}^{n}(X_{i} - \bar{X})^2}\right] \end{aligned}\)

A variância de \(b_0\) pode ser estimada por:

\(\begin{aligned} &\ s^2[b_0] = EQM \left[\frac{1}{n}+\frac{\bar{X}^2} {\sum_{i=1}^{n}(X_{i} - \bar{X})^2}\right] \end{aligned}\)

A estatística \(\frac{b_0 - \beta_0}{s[b_0]}\) segue uma distribuição t de Student, com n-2 graus de liberdade, de modo que o intervalo de confiança de \(\beta_0\) com nível de confiança \(1 - \alpha\) pode ser calculado a partir da expressão abaixo:

\(\begin{aligned} &\ P \left[ -t_{n-2, 1-\alpha/2} \leq \frac{b_0 - \beta_0}{s[b_0]} \leq t_{n-2, 1-\alpha/2}\right] = 1 - \alpha \end{aligned}\)

Portanto o intervalo de confiança de \(\beta_0\) com nível de confiança \(1 - \alpha\) é dado por:

\(\begin{aligned} &\ \boldsymbol{b_0 -t_{n-2, 1-\alpha/2}\ s[b_0] \leq \beta_0 \leq b_0 + t_{n-2, 1-\alpha/2} \ s[b_0]} \end{aligned}\)

19.4.3 Coeficiente de determinação

O coeficiente de determinação é uma medida que indica o quanto os pares de pontos (x, y) estão próximos da reta de regressão. Ele é representado por R² e é calculado pela expressão:

\(\begin{aligned} &\ R^2 = \frac{SQTot - SQE}{SQTot} = \frac{SQR}{SQTot} = 1- \frac{SQE}{SQTot} \end{aligned}\)

\(0 \le R^2 \le 1\) e pode ser interpretado como a proporção da variação de Y que está associada à variável X. Quando os pontos estão alinhados, o valor de R² é igual a 1. Quando não há nenhuma relação linear entre X e Y (inclinação da reta igual a 0), R² é igual a 0. Em geral R² estará entre esses dois limites. Quanto mais próximos de uma linha reta estão os pontos, mais próximo de 1 será o valor de R².

19.4.4 Validação do modelo de regressão linear

Os conteúdos desta seção e da seção 19.5 podem ser visualizados neste vídeo.

O modelo de regressão linear possui as seguintes suposições:

1. a função de regressão é linear;
   
2. os erros são independentes e seguem uma distribuição normal com média igual a 0 e variância constante, \(\sigma^2\).

A análise dos resíduos é um dos principais recursos para verificarmos a validade de um modelo de regressão linear. O resíduo \(e_i\) é igual à diferença entre o valor observado e o valor previsto pela reta de regressão:

  \(e_i = Y_i - \hat{Y_i}\)

Os resíduos podem ser considerados como erros observados e não como os erros reais que seriam dados pela expressão \(\epsilon_i = Y_i - E[Y_i]\), onde \(E[Y_i] = \beta_0 + \beta_1 x_i\)

Se o modelo de regressão linear for adequado, os resíduos devem refletir as suposições do modelo de regressão linear.

Frequentemente a análise de resíduos é realizada com os resíduos padronizados, que são obtidos pela divisão de cada resíduo pela seu desvio padrão, \(\sigma\), que é estimado pela raiz quadrada do EQM. Logo:

\(\begin{aligned} &\ \text{resíduo padronizado} = \frac{e_i}{\sqrt{EQM}} \end{aligned}\)

Diagramas de dispersão dos resíduos (ou resíduos padronizados) em relação à variável independente ou valores previstos pela reta de regressão podem mostrar visualmente violações das suposições do modelo de regressão linear.

A figura 19.10 mostra um diagrama de dispersão dos resíduos padronizados x valores previstos pela reta de regressão para cada um dos pontos da amostra do conjunto de dados Prestige.

Nesse diagrama, podemos observar que os resíduos não parecem seguir algum padrão que pudesse indicar um outro tipo de relacionamento entre a variável dependente e a variável independente, ou alguma dependência entre os resíduos. Também não há evidência de que a dispersão dos resíduos se altera para os diversos valores esperados pela reta de regressão. Um diagrama de comparação de quantis (normal probability plot) nos permitirá verificar se os resíduos padronizados seguem uma distribuição normal ou não.

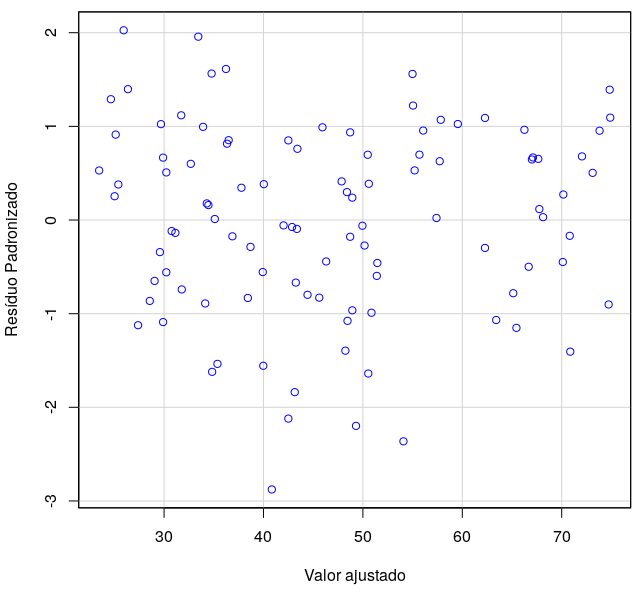
Figura 19.10: Diagrama de dispersão dos resíduos padronizados x valores previstos pela reta de regressão para cada um dos pontos da amostra do conjunto de dados Prestige.

Quando os resíduos seguem uma distribuição normal, espera-se que 5% dos resíduos padronizados sejam menores que -1,96 ou maiores do que 1,96. No gráfico acima, verifica-se que alguns resíduos padronizados são menores do que -2 e um resíduo é maior do que 2, mas a grande maioria dos resíduos padronizados estão situados entre -1,96 e 1,96, não indicando que haja pontos que estejam muito fora dos valores previstos pelo modelo de regressão linear.

Outros diagnósticos para o modelo de regressão linear como identificação de casos influentes e omissão de variáveis importantes estão além do escopo deste texto.

19.5 Análise de Regressão no R Commander

Vamos realizar a análise da relação entre as variáveis prestige e education do conjunto de dados Prestige. Após carregarmos o conjunto de dados, selecionamos no menu do R Commander a opção:

\[\text{Estatísticas} \Rightarrow \text{Ajuste de Modelos} \Rightarrow \text{Regressão Linear}\]

Na tela Regressão Linear (figura 19.11), selecionamos a variável resposta ou variável dependente (prestige) e a variável explicativa ou independente (education). É preciso atribuir um nome ao modelo que será construído (seta verde na figura 19.11). Esse nome será usado para referenciar os componentes desse modelo mais adiante.

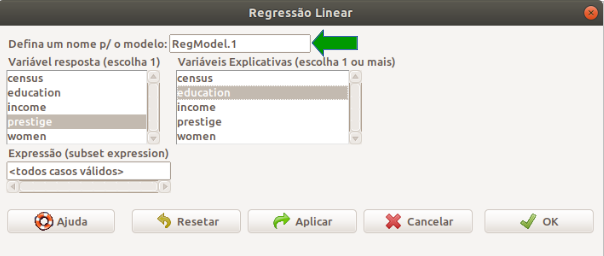
Figura 19.11: Configuração para a análise de regressão linear de prestige x education no conjunto de dados Prestige.

Ao clicarmos no botão OK, os comandos abaixo serão executados, com os resultados apresentados a seguir.

RegModel.1 <- lm(prestige~education, data=Prestige)
summary(RegModel.1)

## 
## Call:
## lm(formula = prestige ~ education, data = Prestige)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -26.0397  -6.5228   0.6611   6.7430  18.1636 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -10.732      3.677  -2.919  0.00434 ** 
## education      5.361      0.332  16.148  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.103 on 100 degrees of freedom
## Multiple R-squared:  0.7228, Adjusted R-squared:   0.72 
## F-statistic: 260.8 on 1 and 100 DF,  p-value: < 2.2e-16

Inicialmente, o resumo do modelo mostra a função usada para gerar o modelo de regressão:

lm(formula = prestige ~ education, data = Prestige)

lm significa linear model e é o nome da função que deve ser usada para criar um modelo de regressão linear. O primeiro argumento da função lm é formula, a qual deve iniciar com uma variável dependente seguida do sinal ~ e da variável independente. O outro argumento, data, define o conjunto de dados a ser utilizado.

Em seguida, são mostrados alguns quantis dos resíduos do modelo, seguidos dos coeficientes da reta de regressão, onde são mostrados a estimativa pelo método dos mínimos quadrados, o erro padrão, o valor da estatística t e o valor de p para cada um dos dois coeficientes. Verificamos que os dois coeficientes são estatisticamente diferentes de zero. Na parte final, o resumo do modelo mostra o valor de R², o valor da estatística F para o modelo de regressão e o valor de p para o modelo.

Para obtermos os intervalos de confiança para os coeficientes do modelo, utilizamos a seguinte opção do menu:

\[\text{Modelos} \Rightarrow \text{Intervalos de confiança}\]

Em seguida, digitamos o nível de confiança desejado e clicamos em OK (figura 19.12).

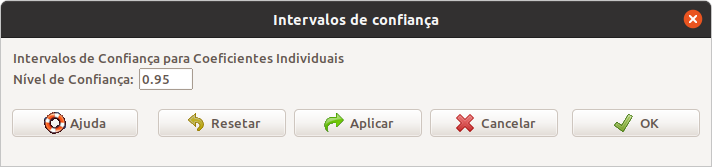
Figura 19.12: Especificação do nível de confiança dos intervalos de confiança dos coeficientes do modelo de regressão linear.

O comando a seguir é executado e gera os intervalos de confiança para a interseção e a inclinação do modelo de regressão linear.

Confint(RegModel.1, level=0.95)

##               Estimate      2.5 %    97.5 %
## (Intercept) -10.731982 -18.027220 -3.436744
## education     5.360878   4.702223  6.019533

Para obtermos alguns gráficos diagnósticos do modelo gerado, selecionamos a opção:

\[\text{Modelos} \Rightarrow \text{Gráficos} \Rightarrow \text{Diagnósticos Gráficos Básicos}\]

Os gráficos gerados são mostrados na figura 19.13.

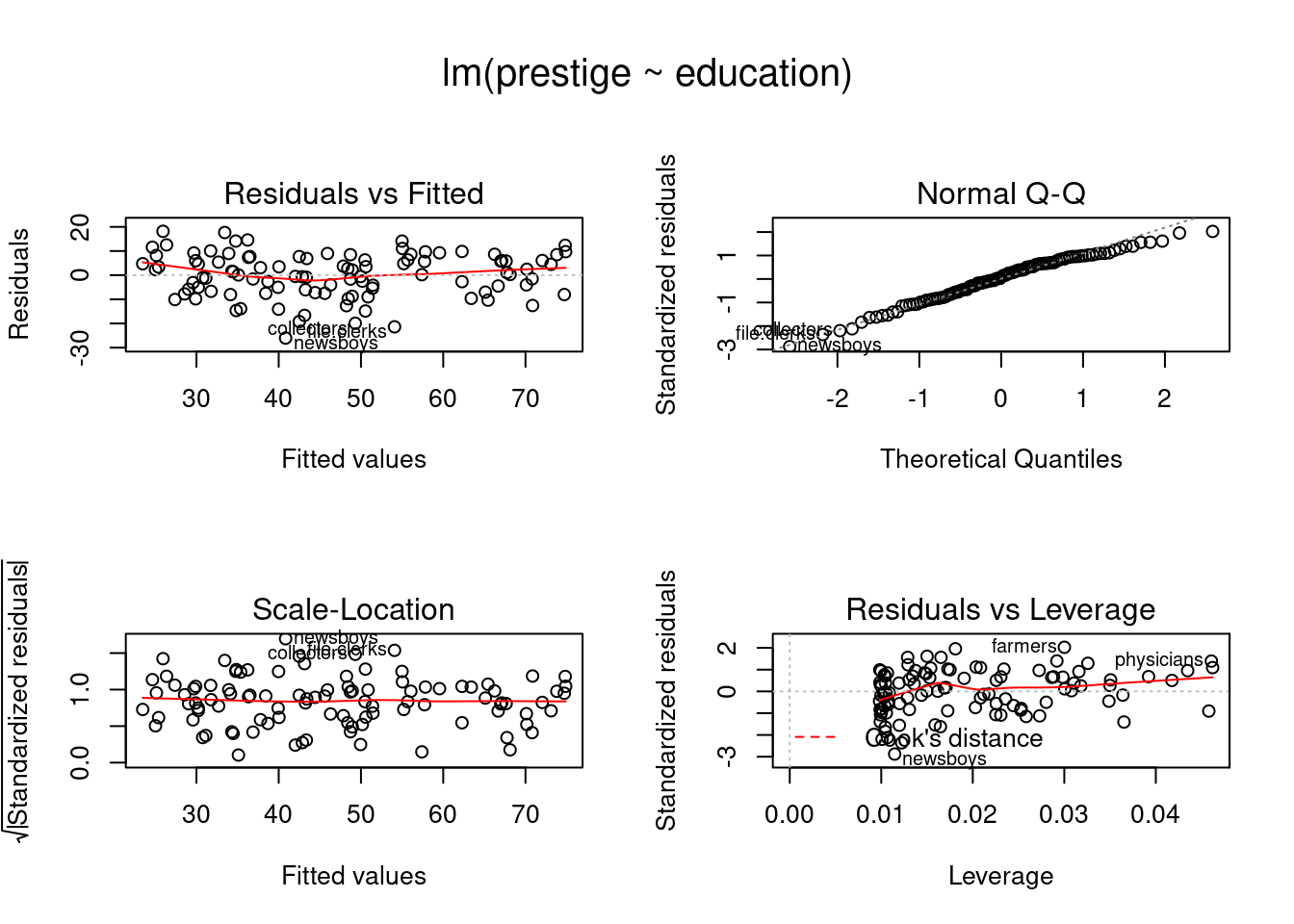
Figura 19.13: Diagnósticos para o modelo de análise de regressão linear de prestige x education para o conjunto de dados Prestige.

O primeiro gráfico na parte superior à esquerda mostra os resíduos x valores ajustados pela reta de regressão. O gráfico da parte superior à direita é o gráfico de comparação de quantis (normal probability plot) dos resíduos padronizados e o gráfico da parte inferior à esquerda é o diagrama de dispersão da raiz quadrada dos resíduos padronizados x valores ajustados pela reta de regressão. Os três gráficos não indicam desvios importantes da hipótese de normalidade, indicam que a variância é uniforme para cada valor ajustado e que os resíduos são independentes. A explicação para o último gráfico está além do escopo deste texto.

19.6 Coeficiente de correlação linear

Os conteúdos desta seção e de suas subseções podem ser visualizados neste vídeo.

Voltando à figura 19.1 que mostra o diagrama de dispersão relacionando as variáveis prestígio (prestige) e nível educacional (education), uma medida do relacionamento linear entre as duas variáveis é dada pelo coeficiente de correlação linear de Pearson, que é calculado pela fórmula:

\[\begin{align} r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2\ \sum_{i=1}^{n} (y_i - \bar{y})^2 }} \tag{19.19} \end{align}\]

O coeficiente de correlação pode assumir um valor entre -1 e +1. Se maiores valores de uma variável x, em geral, correspondem a valores maiores de outra variável y e valores menores de x, em geral, correspondem a menores valores de y, então o coeficiente de correlação é maior que zero (figura 19.14a), sendo igual a 1 quando os valores de x e y estão perfeitamente alinhados em uma reta com inclinação positiva. Se maiores valores de x, em geral, correspondem a valores menores de y e valores menores de x, em geral, correspondem a maiores valores de y, então o coeficiente de correlação é menor que zero (figura 19.14b), sendo igual a -1 quando os valores de x e y estão perfeitamente alinhados em uma reta com inclinação negativa. Quando não há uma tendência de valores de y variarem de acordo com os valores de x, o coeficiente de correlação é zero (figura 19.14c).

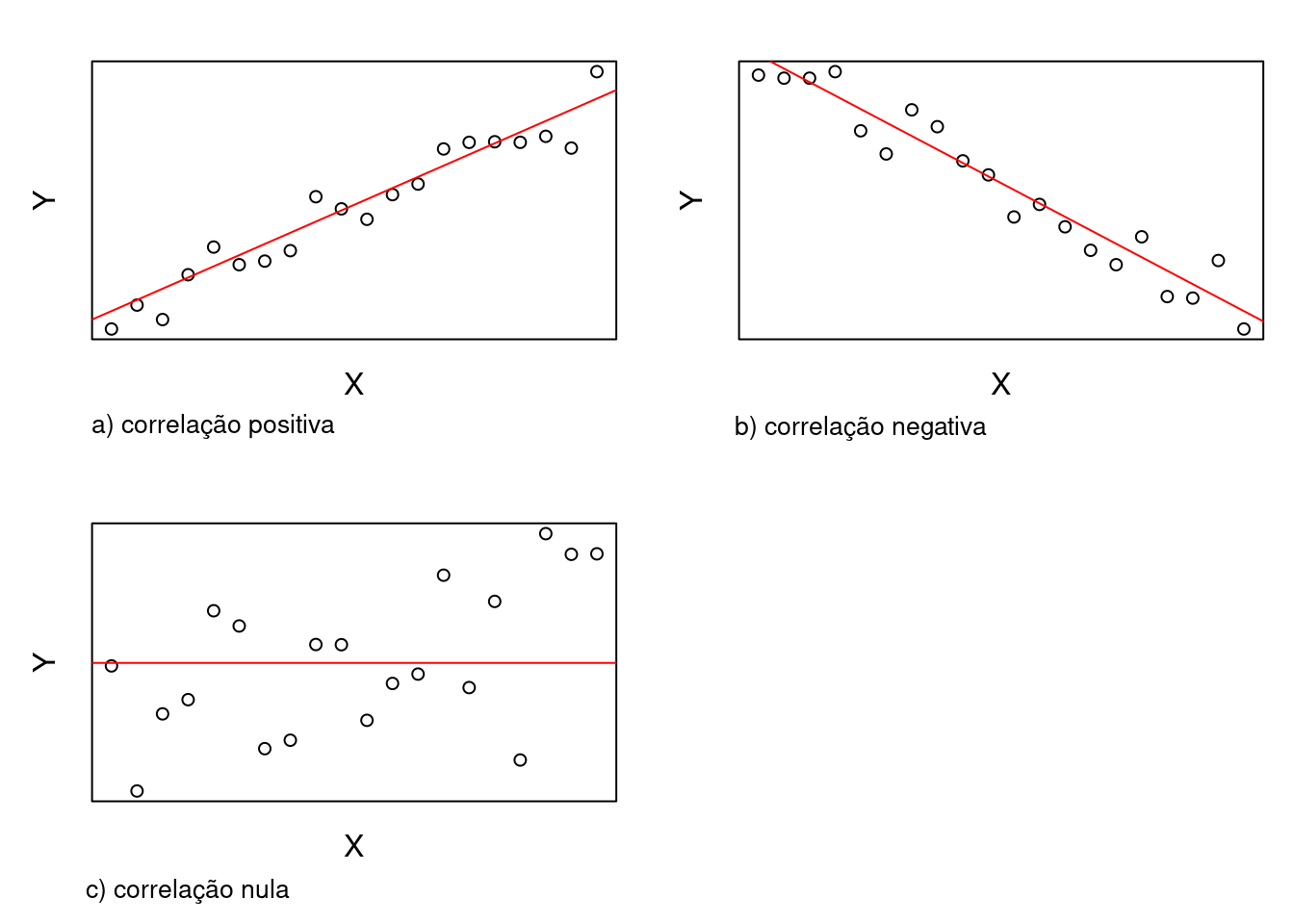
Figura 19.14: Relações lineares entre as variáveis x e y: a) correlação linear positiva, b) correlação linear negativa, c) correlação nula.

O quadrado do coeficiente de correlação linear é igual ao coeficiente de determinação do modelo de regressão linear simples.

19.6.1 Teste de hipótese bilateral e intervalos de confiança para o coeficiente de correlação

O teste de hipótese bilateral e o cálculo do intervalo de confiança para o coeficiente de correlação linear partem da suposição de que os valores das variáveis correlacionadas (vamos chamá-las de X e Y) proveem aleatoriamente de uma distribuição normal bivariada. Vamos chamar o coeficiente de correlação real de \(\rho\). Vamos considerar duas situações:

\(1)\ H_0: \rho = 0;\ \ \ \ \ \ H_1: \rho \neq 0\)

Para testarmos a hipótese nula de que o coeficiente de correlação é zero, pode-se mostrar que a estatística apropriada é:

\[\begin{align} t = r\ \sqrt{\frac{n-2}{1-r^2}} \tag{19.20} \end{align}\]

Quando H₀ for verdadeira, t segue uma distribuição t de Student, com n-2 graus de liberdade, e o teste de hipótese é realizado da forma conhecida.

\(2)\ H_0: \rho = \rho_0;\ \ \ \ \ \ H_1: \rho \neq \rho_0\)

Um outro enfoque deve ser utilizado para realizar um teste de hipótese quando a hipótese nula se referir a um valor de coeficiente de correlação diferente de zero. O coeficiente de correlação, r, deve ser transformado para z_r como se segue (transformação de Fisher):

\[\begin{align} z_r = \frac{1}{2} ln \frac{1+r}{1-r} \tag{19.21} \end{align}\]

onde ln é o logaritmo natural (base e). Pode-se mostrar que, sob a hipótese nula e para amostras não muito pequenas, z_r é aproximadamente normalmente distribuído com média igual a \(z_{\rho_0} = \frac{1}{2} ln \frac{1+\rho_0}{1-\rho_0}\), e desvio padrão estimado igual a \(\sqrt{\frac{1}{n-3}}\). Para testarmos então a hipótese nula de que \(\rho = \rho_0 \neq 0\), a estatística a ser utilizada é:

\[\begin{align} z = \frac{z_r - z_{\rho_0}}{\sqrt{1 / (n-3)}} \tag{19.22} \end{align}\]

que segue uma distribuição normal padrão.

Para calcularmos o intervalo de confiança (\(1-\alpha\)) para \(\rho\), inicialmente calculamos o intervalo de confiança para \(z_\rho\), dado por:

\[\begin{align} \left[z_r - z_{1-\alpha/2}\ \sqrt{\frac{1}{n-3}},\ z_r + z_{1-\alpha/2}\ \sqrt{\frac{1}{n-3}}\right] \tag{19.23} \end{align}\]

Os limites do intervalo de confiança para \(\rho\) são obtidos a partir dos limites de \(z_\rho\) acima, usando a inversa da relação (19.21):

\(\begin{aligned} &\ r = \frac{e^{2z_{r}}-1}{e^{2z_{r}}+1} \end{aligned}\)

e substituindo \(z_{r}\) sucessivamente pelos dois limites obtidos na expressão (19.23).

19.6.2 Cálculo do coeficiente de correlação no R Commander

Para calcularmos o valor, o intervalo de confiança e realizarmos um teste de hipótese para o coeficiente de correlação entre duas variáveis numéricas no R Commander, utilizamos a opção:

\[\text{Estatísticas} \Rightarrow \text{Resumos} \Rightarrow \text{Teste de Correlação...}\]

Na tela de configuração do teste, o usuário deve selecionar as variáveis que serão correlacionadas, o tipo de correlação e o tipo de teste de hipótese (figura 19.15).

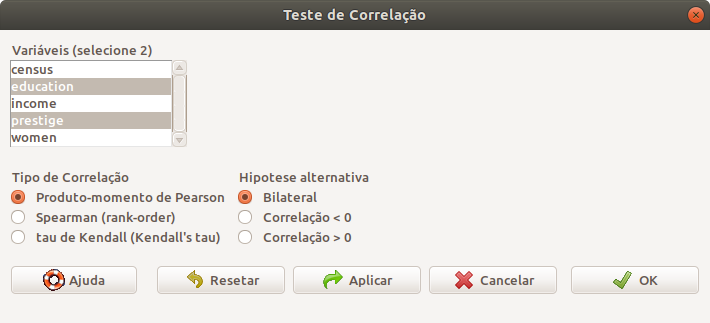
Figura 19.15: Seleção das duas variáveis que serão correlacionadas, tipo de coeficiente de correlação (Pearson neste exemplo) e se o teste é bilateral ou unilateral.

A função executada é mostrada a seguir. Os resultados mostram o valor de p (< 2,2 . 10^-16), o valor do coeficiente de correlação (0,85) e o intervalo de confiança ao nível de 95%.

with(Prestige, cor.test(education, prestige, alternative="two.sided", 
                        method="pearson"))

## 
##  Pearson's product-moment correlation
## 
## data:  education and prestige
## t = 16.148, df = 100, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.7855899 0.8964367
## sample estimates:
##       cor 
## 0.8501769

Caso desejássemos outro nível de confiança, bastaria alterarmos a função acima, acrescentando o parâmetro conf.level. Por exemplo, se desejássemos que o nível de significância do teste fosse 10% (nível de confiança = 90%), utilizaríamos a função cor.test da seguinte forma:

with(Prestige, cor.test(education, prestige, alternative="two.sided",
                        method="pearson", conf.level = .90))

## 
##  Pearson's product-moment correlation
## 
## data:  education and prestige
## t = 16.148, df = 100, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 90 percent confidence interval:
##  0.7974164 0.8900372
## sample estimates:
##       cor 
## 0.8501769

O coeficiente de correlação linear indica o grau de relação linear entre duas variáveis numéricas. Quando ele for zero, significa que uma variável não é linearmente relacionada à outra, mas isso não quer dizer que não exista nenhum relacionamento entre essas variáveis. Há muitos outros tipos de relações entre duas variáveis que não são lineares. A figura 19.16 mostra três possíveis relações: senoidal, quadrática e exponencial.

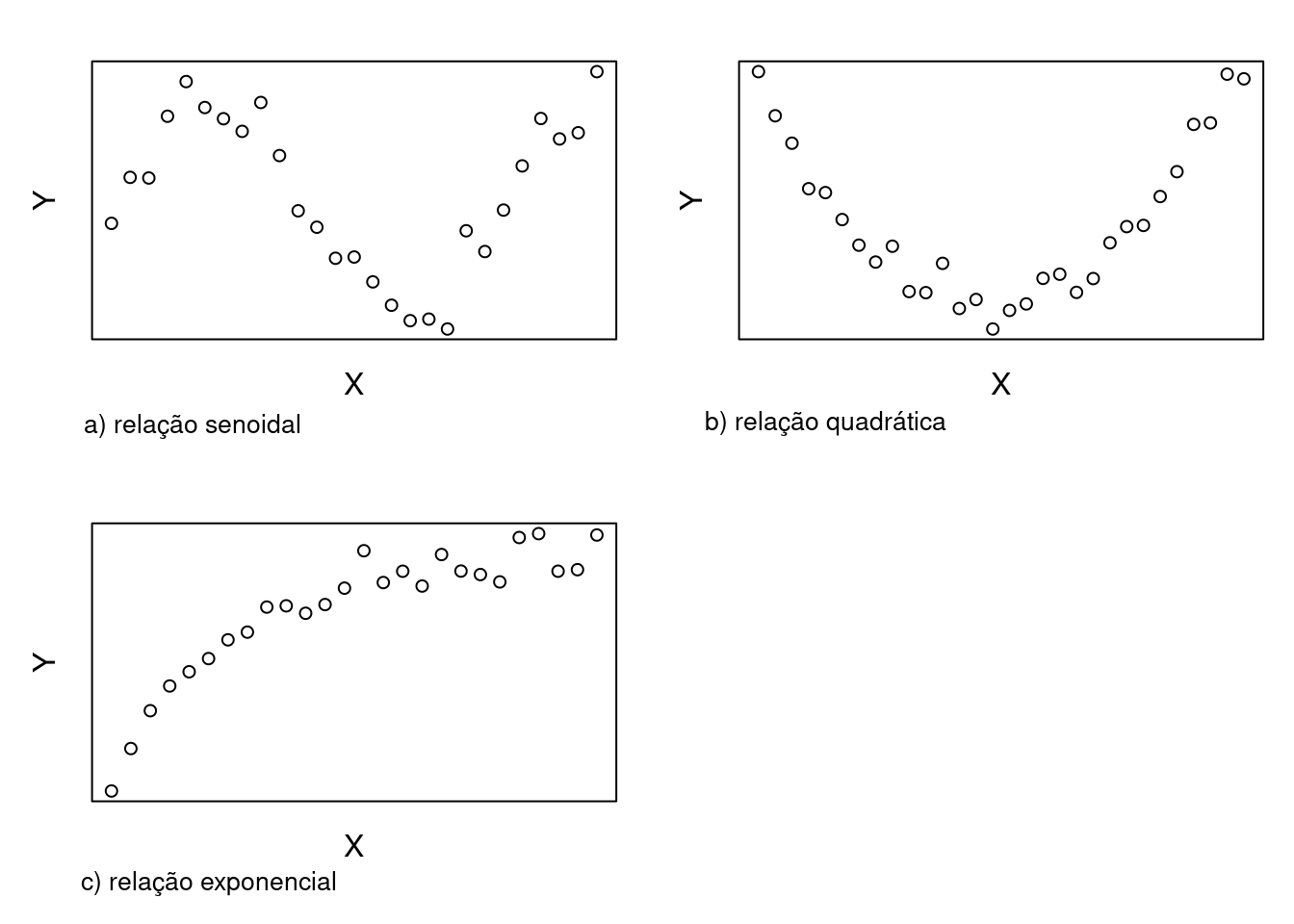
Figura 19.16: Exemplos de relações não lineares entre duas variáveis.

19.6.3 Coeficiente de correlação de Spearman

Caso as variáveis não possuam uma distribuição conjunta normal e não haja alguma transformação das variáveis que torne a distribuição conjunta das variáveis transformadas normal, então pode-se recorrer a métodos não paramétricos para verificar o relacionamento linear entre as variáveis. Um dos métodos mais frequentemente utilizados é o coeficiente de correlação de postos de Spearman. Para o cálculo do coeficiente de Spearman, postos são atribuídos aos valores das variáveis, de maneira análoga ao teste não paramétrico de Wilcoxon para duas amostras (seção 16.2.5) e, então, o coeficiente de correlação é calculado de acordo com a equação (19.19), utilizando os postos das variáveis e não os valores originais.

Pacotes estatísticos realizam testes de hipótese para a hipótese de correlação nula entre os postos das variáveis.

Para realizarmos o teste de correlação de Spearman para as variáveis prestige e education, basta selecionarmos as variáveis, o tipo de teste e se é bilateral ou não, conforme a figura 19.17, acessada por meio da opção.

\[\text{Estatísticas} \Rightarrow \text{Resumos} \Rightarrow \text{Teste de Correlação...}\]

Figura 19.17: Configuração para o cálculo do coeficiente de correlação de Spearman.

A função executada (cor.test) é mostrada abaixo seguida dos resultados.

with(Prestige, cor.test(education, prestige, alternative="two.sided", 
                        method="spearman"))

## 
##  Spearman's rank correlation rho
## 
## data:  education and prestige
## S = 32100, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.8184923

19.7 Exercícios

1. Com o conjunto de dados CrohnD do pacote robustbase (GPL-2 | GPL-3), faça as atividades abaixo.

   1. Veja a ajuda do conjunto de dados.
   2. Faça um diagrama de dispersão do índice de massa corporal (IMC) por peso, com a reta de regressão superposta.
   3. Construa um modelo de regressão linear simples do IMC em função do peso. Identifique os valores dos coeficientes de regressão, o coeficiente de determinação e o valor de p do modelo. Comente sobre o poder explicativo do modelo.
   4. Obtenha os diagnósticos gráficos básicos do modelo e comente os gráficos dos resíduos x valores ajustados pela reta de regressão, o gráfico de comparação de quantis dos resíduos padronizados e o diagrama de dispersão da raiz quadrada dos resíduos padronizados x valores ajustados.
   5. Obtenha os intervalos de confiança para os coeficientes do modelo de regressão.

2. Com o conjunto de dados Pima.te do pacote MASS (GPL-2 | GPL-3), faça as atividades abaixo.

   1. Veja a ajuda do conjunto de dados.
   2. Faça um diagrama de dispersão da glicose por índice de massa corporal (IMC), com a reta de regressão superposta.
   3. Construa um modelo de regressão linear simples da glicose em função do IMC. Identifique os valores dos coeficientes de regressão, o coeficiente de determinação e o valor de p do modelo. Comente sobre o poder explicativo do modelo.
   4. Comparando com o modelo do exercício anterior e da conhecida fórmula para o cálculo do IMC, comente o fato de o coeficiente de determinação do modelo do exercício 1 ser bem maior do que o deste exercício.
   5. Obtenha os diagnósticos gráficos básicos do modelo e comente os gráficos dos resíduos x valores ajustados pela reta de regressão, o gráfico de comparação de quantis dos resíduos padronizados e o diagrama de dispersão da raiz quadrada dos resíduos padronizados x valores ajustados.
   6. Obtenha os intervalos de confiança para os coeficientes do modelo de regressão.

Referências

Costa Neto, Pedro Luiz de Oliveira. 1977. Estatística. São Paulo, Brazil: Editora Edgard Blücher LTDA.

Durmus, E, T Kivrak, F Gerin, M Sunbul, I Sari, and O Erdogan. 2015. “Relações Neutrófilo-Linfócito e Plaqueta-Linfócito Como Preditores de Insuficiência Cardíaca.” Arquivos Brasileiros de Cardiologia 105 (6): 606–13.

Kutner, MH, CJ Nachtsheim, J Neter, and W Li. 2005. Applied Linear Statistical Models. 5th ed. Boston: McGraw-Hill/Irwin.