10 Distribuições de variáveis aleatórias discretas

10.1 Introdução

Um dos conceitos fundamentais em estatística é o de distribuição de probabilidades.

Como visto no capítulo anterior, uma distribuição de probabilidades, também conhecida como função de probabilidade, associa um valor de probabilidade a cada valor possível de uma variável aleatória discreta. Portanto uma variável aleatória discreta X, que possa assumir k valores diferentes, tem associada a cada valor X = x_i, i = 1, 2, …, k, uma probabilidade definida por P(X = x_i) = p_i. Existem diversas funções de probabilidades teóricas que são usadas para modelar problemas envolvendo variáveis discretas.

Quando assumimos uma distribuição teórica para representar o resultado de um experimento, estamos descrevendo um modelo estatístico para o problema. Este capítulo apresenta três distribuições de probabilidades para variáveis discretas bastante utilizadas: binomial, Poisson e geométrica.

10.2 Distribuição binomial

Os conteúdos desta seção e de suas subseções podem ser visualizados neste vídeo.

A distribuição binomial é uma das distribuições de probabilidades mais utilizadas para modelar fenômenos aleatórios discretos. A distribuição binomial descreve as probabilidades do número de sucessos em um certo número de experimentos (n) se as seguintes condições são satisfeitas:
1. O número de experimentos n é fixo;
2. Cada experimento é independente;
3. O resultado de cada experimento é um de dois possíveis desfechos (sucesso ou fracasso, 0 ou 1, etc). Experimentos desse tipo são conhecidos como experimentos de Bernoulli;
4. A probabilidade de sucesso p é a mesma em cada experimento.

Se as condições acima são satisfeitas, então X possui uma distribuição binomial com parâmetros n e p, e podemos abreviadamente representá-la por X ~ B(n, p).

Recordando, a tabela 8.3 do capítulo 8 compara o risco de desenvolvimento de diabetes mellitus em pessoas com IMC (Índice de Massa Corporal) na faixa de 14,5 - 24,9 kg/m² com pessoas com IMC > 30 kg/m². A distribuição binomial é utilizada para modelar o número de pessoas que desenvolvem diabetes em cada uma dessas duas categorias de IMC. Tomando o grupo de pessoas com IMC > 30 kg/m², por exemplo, vimos que a proporção de pessoas que desenvolveram diabetes mellitus no estudo foi de:

\(\begin{aligned} \ R_{IMC>30}= \frac{156}{1384} = 11\% \end{aligned}\)

Assim poderíamos utilizar uma distribuição binomial para modelar o número de pessoas com IMC > 30 kg/m² que desenvolverão diabetes mellitus. Aplicando as condições 1 a 4 acima, esse modelo seria válido, se:
1. fixamos o número de experimentos, ou seja, o número de pessoas com IMC > 30 kg/m² que iremos acompanhar. No caso da tabela 3, faremos n = 1384;
2. cada experimento é independente, ou seja, o fato de uma pessoa do grupo desenvolver diabetes mellitus independe do desfecho nas outras pessoas;
3. o desfecho de cada experimento é uma variável dicotômica; nesse caso, cada pessoa desenvolve ou não diabetes mellitus;
4. a probabilidade do desfecho p é a mesma em cada experimento. Aqui consideraremos que a probabilidade de ocorrência de diabetes mellitus é a mesma para todas as pessoas no grupo estudado. Essa probabilidade foi estimada como 0,11.

Portanto o número de pessoas do grupo com IMC > 30 kg/m² que terão diabetes mellitus (X) é uma variável aleatória discreta que segue uma distribuição binomial, com parâmetros n = 1384 e p = 0,11. Então:

\(X \sim B(1384; 0,11)\)

A variável aleatória X pode assumir os valores 0, 1, 2, 3, …, 1384, ou seja, para as 1384 pessoas com IMC > 30 kg/m², pode acontecer que nenhuma pessoa fique doente, ou 1, 2, 3, ou até todas as pessoas venham a desenvolver diabetes mellitus. Nesse estudo em particular, 156 pessoas ficaram doentes, mas qualquer um dos valores entre 0 e 1384 poderia ser observado.

10.2.1 Probabilidades de uma distribuição binomial

Para uma variável aleatória que segue a distribuição binomial, as probabilidades de ocorrência de cada valor k entre 0 e n (número de experimentos) são dadas pela seguinte expressão:

\[\begin{align} P(X=k)={n \choose k} p^{k} q^{n-k}=\frac{n!}{k!(n-k)!}p^{k} q^{n-k} \tag{10.1} \end{align}\]

Na expressão acima, q = 1 - p. O símbolo ! significa fatorial.

Assim \(n! = n .(n-1) . (n-2) … 3 . 2 .1\).

Para o exemplo da seção anterior, teríamos:

\(\begin{aligned} &\ P(X=k)={1384 \choose k} 0,11^{k} 0,89^{1384-k}=\frac{1384!}{k!(1384-k)!}0,11^{k} 0,89^{1384-k} \end{aligned}\)

Com a fórmula acima, poderíamos calcular a probabilidade de nenhuma pessoa desenvolver o diabetes mellitus (k = 0), 1 pessoa (k = 1) desenvolver a doença e assim por diante. Apenas como ilustração, a probabilidade de nenhuma pessoa desenvolver a doença será:

\(\begin{aligned} \ P(X=0)=\frac{1384!}{0!(1384-0)!} 0,11^{0} 0,89^{1384-0}=9,03\ 10^{-71}, \end{aligned}\)

uma probabilidade extremamente baixa.

Vamos utilizar o R para estudarmos um pouco mais a distribuição binomial. Vamos utilizar uma distribuição binomial com menos experimentos do que o exemplo anterior. Vamos considerar a seguinte situação hipotética: 20 pessoas foram submetidas a uma cirurgia cuja probabilidade de sucesso é de 40%, ou seja, p = 0,4. Quais seriam as probabilidades de 1, 2, 3, ou todas as 20 cirurgias serem bem sucedidas?

Considerando cada cirurgia como um experimento de Bernoulli, o número de sucessos em 20 cirurgias (X) será uma variável aleatória com distribuição binomial com n = 20 e p = 0,4. Logo:

\(\begin{aligned} &\ P(X=k)=\frac{20!}{k!(20-k)!}0,4^k 0,6^{20-k} \end{aligned}\)

Substituindo k na fórmula acima por 0, 1, 2, …, 20, obteremos as probabilidades de observarmos 0, 1, 2, …, 20 cirurgias, supondo que a distribuição binomial seja válida para esses 20 experimentos. Em vez de realizarmos esses cálculos manualmente, vamos utilizar o R Commander. A figura 10.1 mostra como acessar o menu que contém diversos recursos para trabalhar com a distribuição binomial. Vamos começar selecionando o item Probabilidades da binomial.

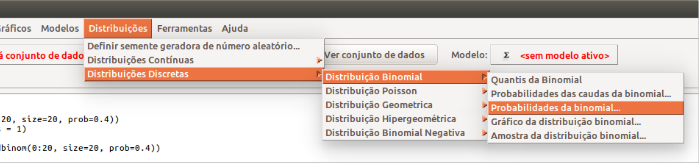
Figura 10.1: Acessando o menu do R Commander que nos permite trabalhar com a distribuição binomial.

Como o nome indica, ao selecionarmos a opção Probabilidades da binomial, somos levados a uma caixa de diálogo na qual especificamos os parâmetros da distribuição binomial que desejamos (figura 10.2). Nesse exemplo, n = 20 (número de experimentos) e p = 0,4. Não esqueçamos que o separador de decimais no R é o ponto, não a vírgula. Ao clicarmos em OK, as probabilidades serão mostradas na console do R Studio (figura 10.3) ou na área de resultados do R Commander.

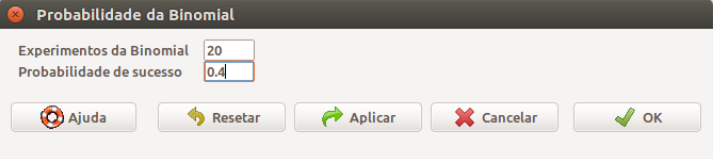
Figura 10.2: Diálogo do R Commander, onde especificamos os parâmetros da binomial. Depois, clicamos em OK para obtermos as probabilidades.

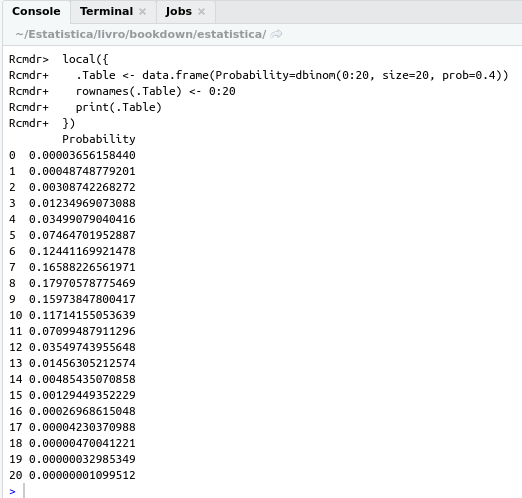
Figura 10.3: Probabilidades de 0, 1, 2, …, 20 cirurgias serem bem sucedidas, supondo que o número de cirurgias bem sucedidas segue a distribuição B(20, 0,4).

Para obtermos o gráfico da distribuição binomial no R Commander, selecionamos a opção:

\[\text{Distribuições} \Rightarrow \text{Distribuições discretas} \Rightarrow \text{Dist. Binomial} \Rightarrow \text{Gráfico Dist. Binomial...}\]

Na caixa de diálogo da figura 10.4, novamente especificamos os parâmetros da distribuição binomial e selecionamos uma das duas opções de gráficos. Selecionando a primeira opção, Gráfico da função de massa, obtemos o gráfico mostrado na figura 10.5.

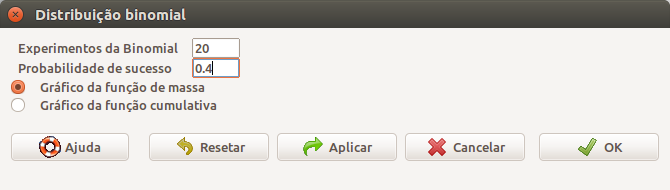
Figura 10.4: Diálogo do R Commander para obtermos os gráficos de uma distribuição binomial.

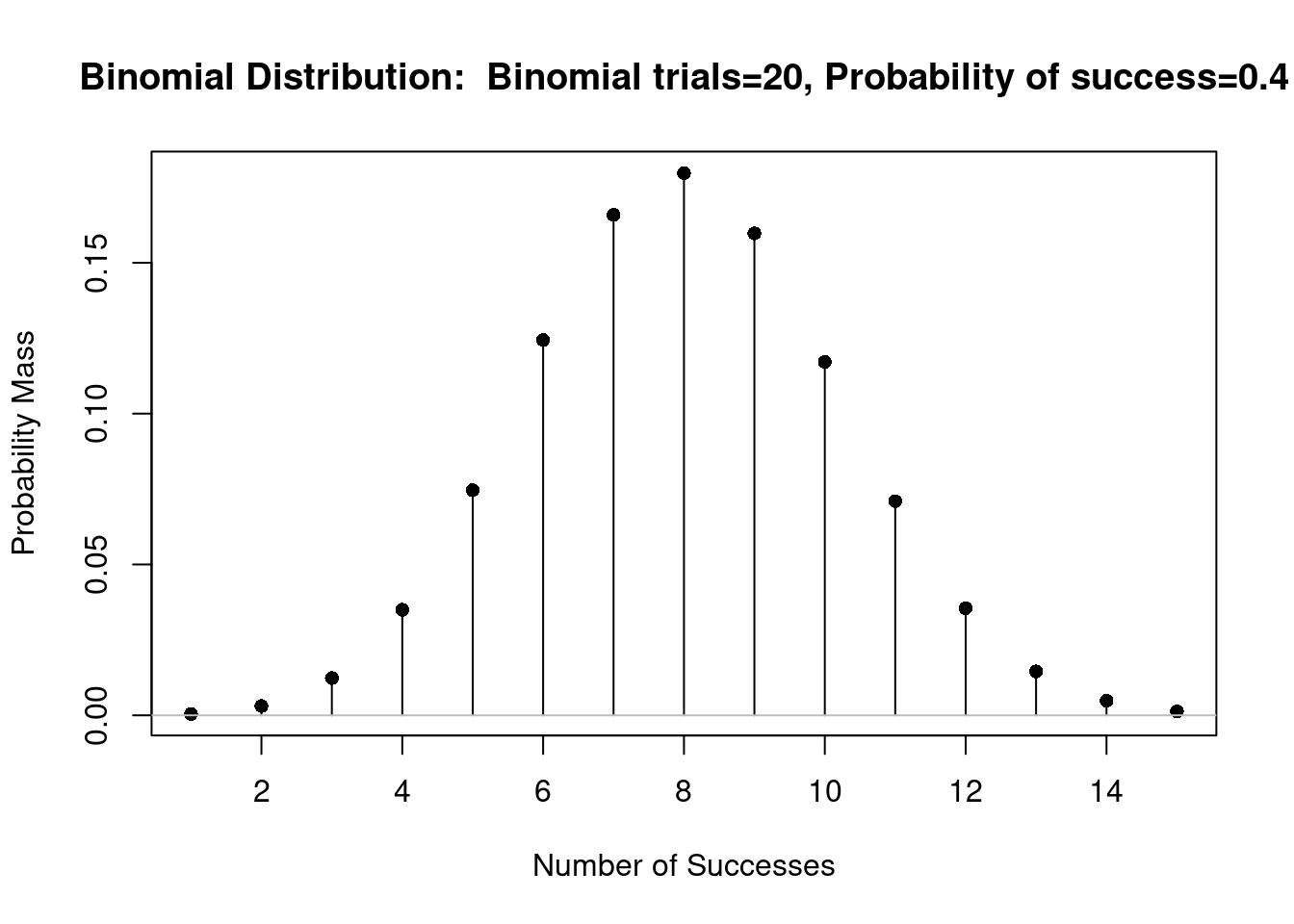
Figura 10.5: Gráfico da distribuição binomial B(20, 0,4).

O gráfico da distribuição de probabilidades mostra, para cada valor possível da variável aleatória, uma linha vertical indicando a probabilidade de ocorrer aquele valor. Assim observem que as probabilidades mostradas correspondem àquelas observadas na listagem da figura 10.3. As probabilidades para os valores acima de 15 e abaixo de 1 não foram mostradas, porque elas são muito pequenas, quando comparadas com os demais valores.

Ao selecionarmos a segunda opção na figura 10.4, Gráfico da função cumulativa, obtemos o gráfico da figura 10.6.

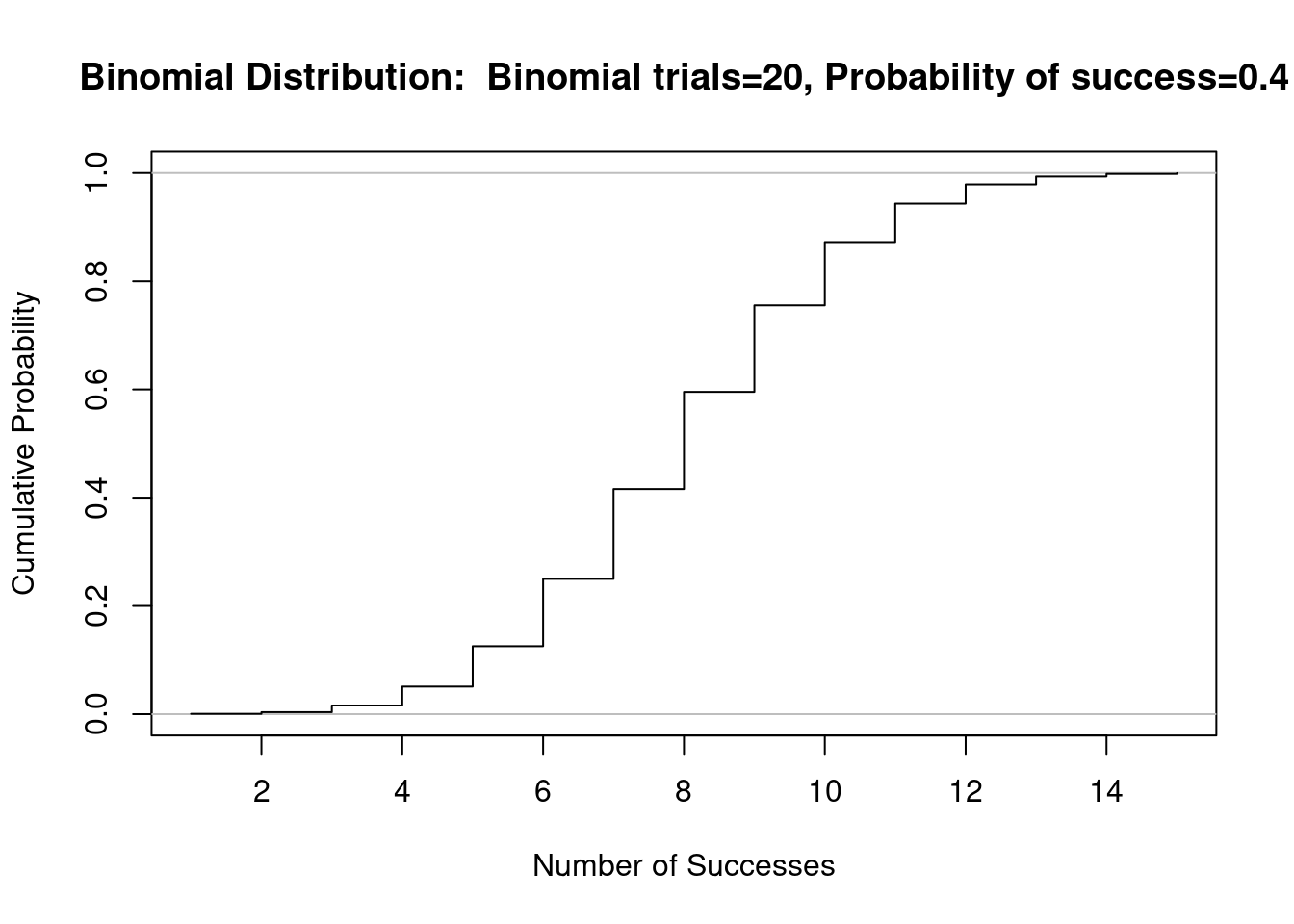
Figura 10.6: Gráfico da distribuição binomial acumulada B(20, 0,4).

O gráfico da distribuição cumulativa, ou acumulada, fornece para cada valor k da variável aleatória discreta, X, a probabilidade de observarmos um número de ocorrências menor ou igual a k. Assim:

\(\begin{aligned} \ Probabilidade Acumulada = F(X=k) = \sum_{0}^{k}P(X=k), 0 \le k \le n \end{aligned}\)

Para ilustrar:

F(0) = P(0) = 0,00003656  
F(1) = P(0) + P(1) = 0,00003656 + 0,00048749 = 0,00052405  
    .......  
F(20) = P(0) + P(1) + P(2) + … + P(20) = 1  

O gráfico da distribuição acumulada possui um formato de escada, pois é sempre crescente. O valor máximo de F é 1 e o valor mínimo é 0.

A figura 10.7 mostra o gráfico da distribuição binomial B(10, 0,5). Observem que o gráfico é simétrico em torno do valor 5. Essa simetria é observada para todas as distribuições binomiais, onde a probabilidade de sucesso é igual a 0,5.

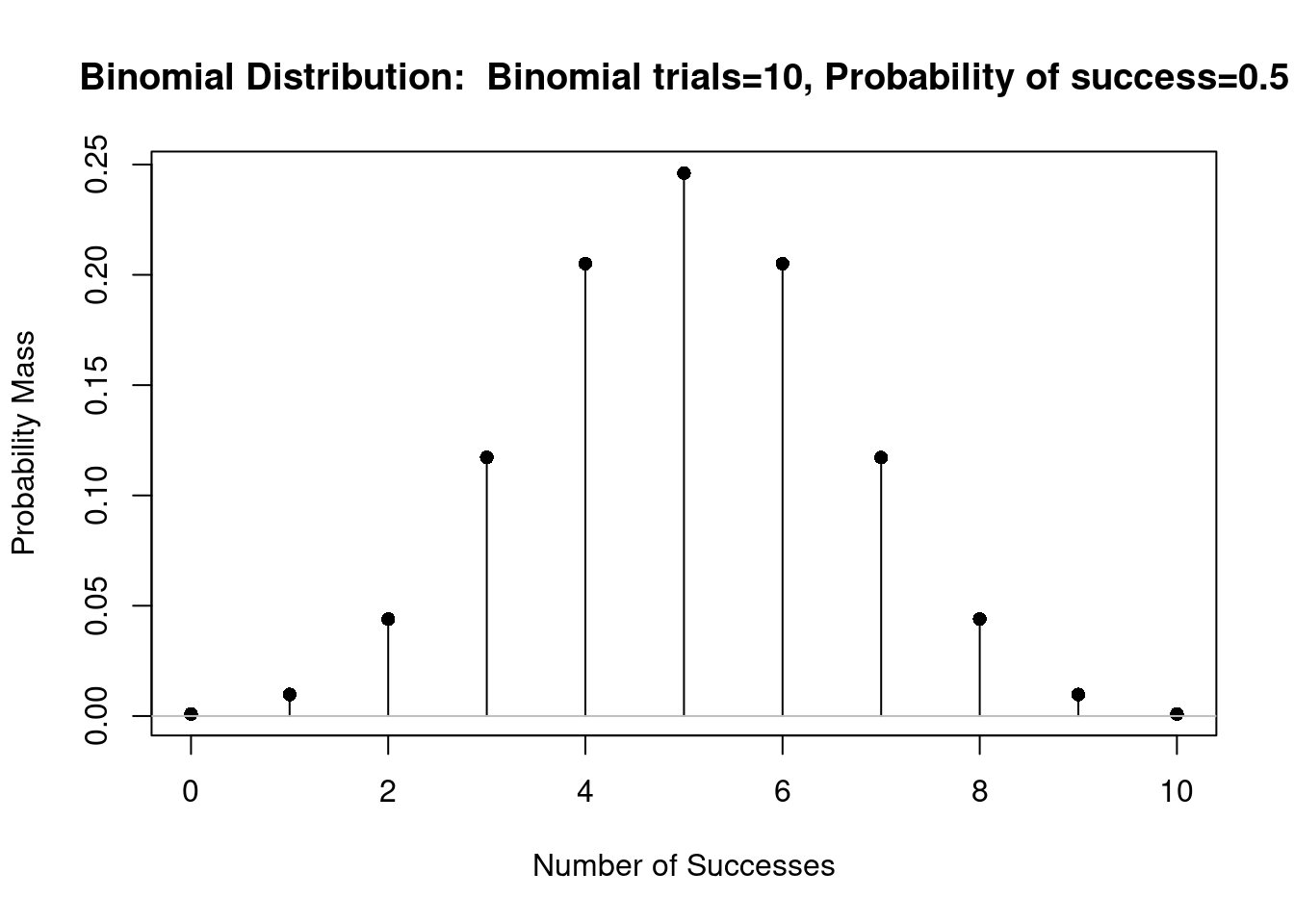
Figura 10.7: Gráfico da distribuição binomial B(10, 0,5).

A figura 10.8 mostra o gráfico da distribuição binomial B(10, 0,1). Observem agora que o gráfico é bastante assimétrico, já que a probabilidade de sucesso é apenas 0,1.

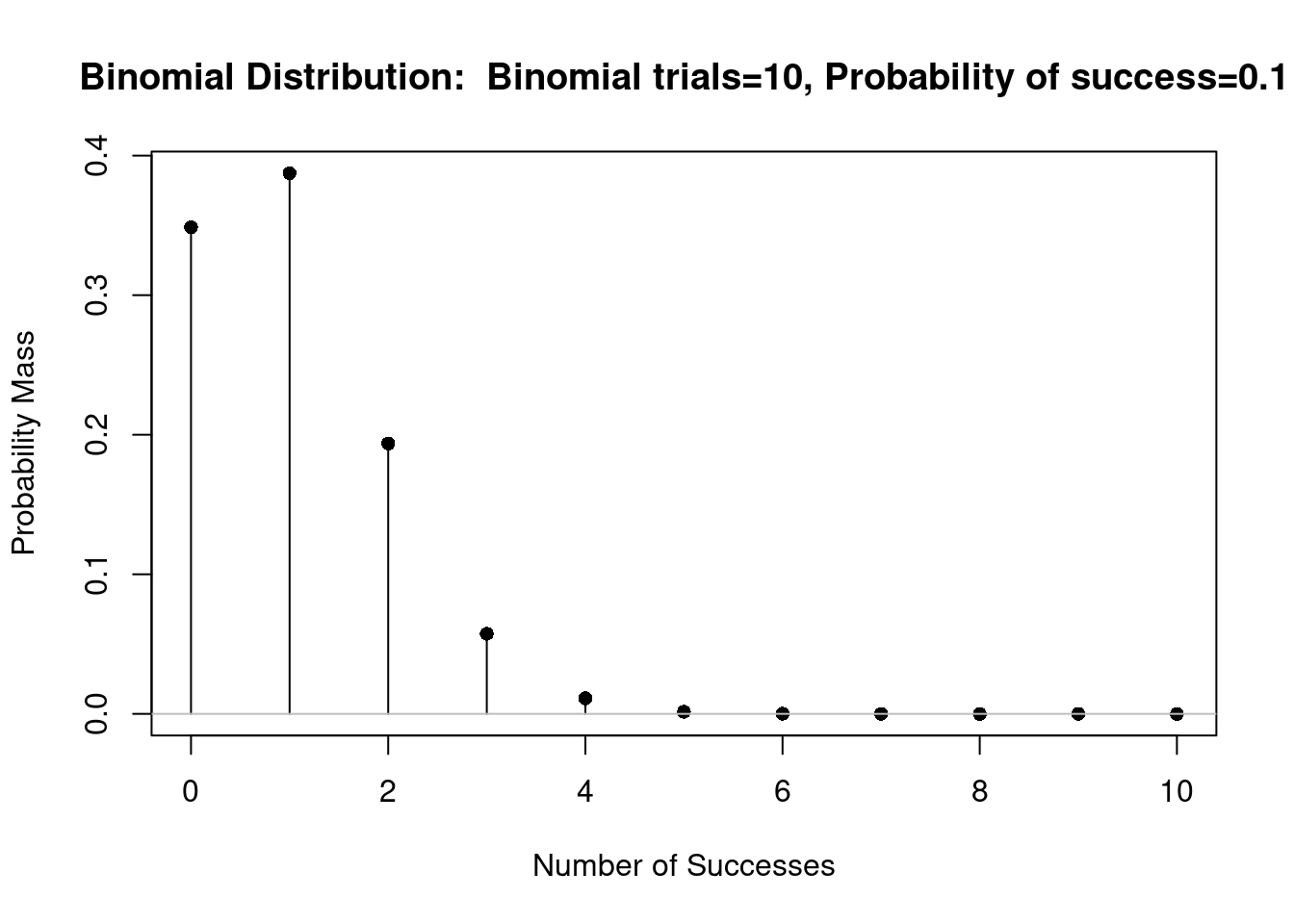
Figura 10.8: Gráfico da distribuição binomial B(10, 0,1).

Caso queiramos obter as probabilidades de ocorrência de até k sucessos, ou seja, a probabilidade acumulada para X = k, utilizamos a segunda opção no menu da figura 10.1: Probabilidades das caudas da binomial. A caixa de diálogo da figura 10.9 nos permite especificar um ou mais valores de k, os parâmetros da binomial e se vamos utilizar a cauda inferior ou superior da distribuição.

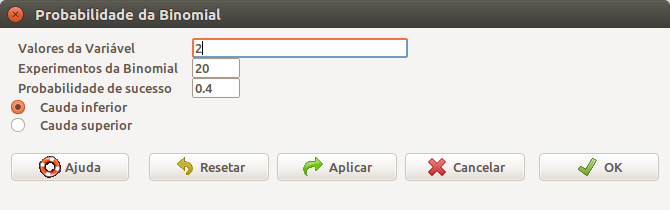
Figura 10.9: Diálogo do R Commander para obtermos as probabilidades das caudas de uma distribuição binomial. Ao selecionarmos a opção cauda inferior, vamos calcular a probabilidade acumulada para o valor especificado (ou valores especifidados) em Valores da Variável.

Para ilustrar, especificamos os parâmetros da distribuição do nosso exemplo B(20, 0,4), vamos fazer k = 2 (ocorrência de 2 cirurgias em 20) em Valores da Variável, e vamos selecionar a opção Cauda inferior. Isso significa que desejamos a probabilidade de ocorrer até 2 cirurgias, ou seja, queremos F(2) = P(0) + P(1) + P(2). O comando gerado pelo R é mostrado abaixo, seguido do resultado de sua execução:

pbinom(c(2), size=20, prob=0.4, lower.tail=TRUE)

## [1] 0.003611472

Ao selecionarmos a opção Cauda superior, vamos calcular a probabilidade de observarmos um número de sucessos acima do valor especificado (ou valores especificados) em Valores da Variável. Observem que a probabilidade fornecida é para o número de ocorrências acima, não igual ou acima, do valor especificado. Isso equivale ao valor de 1-F(k). Como exemplo, na figura 10.10, selecionamos a cauda superior e especificamos vários valores para k em Valores da Variável, separados por vírgula. Isso significa que serão calculadas as probabilidades da cauda superior para cada um dos valores (17, 18, 19, 20)

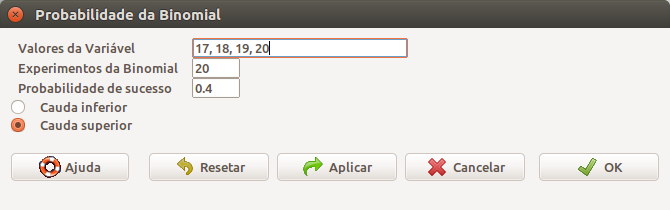
Figura 10.10: Diálogo do R Commander para obtermos as probabilidades das caudas de uma distribuição binomial. Ao selecionarmos a opção Cauda superior, vamos calcular a probabilidade de observarmos um número de sucessos acima do valor especificado (ou valores especificados) em Valores da Variável.

O comando gerado pelo R é mostrado abaixo, seguido das quatro probabilidades, uma para cada um dos quatro valores especificados. Observem que a probabilidade da cauda superior para 20 é zero, porque não pode ocorrer mais de 20 cirurgias bem sucedidas em 20. O valor para k = 19 é igual à probabilidade de observarmos 20 cirurgias (veja o valor de P(20) na figura 10.3). A probabilidade da cauda superior para k = 18 é igual a P(19) + P(20) = 1 – F(18), e assim por diante. A letra e mostrada nesses resultados significa a base 10, não o número irracional e.

pbinom(c(17,18,19,20), size=20, prob=0.4, lower.tail=FALSE)

## [1] 5.041261e-06 3.408486e-07 1.099512e-08 0.000000e+00

Assim como, ao especificarmos um certo número de ocorrências do desfecho de interesse, podemos obter a probabilidade das caudas da distribuição binomial, podemos, inversamente, ao especificar uma probabilidade, obter o número limite de ocorrências nas caudas da distribuição binomial, ou quantis da binomial. Vamos ver alguns exemplos.

A caixa de diálogo para obtermos os quantis da distribuição binomial (figura 10.11) aparece ao selecionarmos a primeira opção no menu da figura 10.1. Ao selecionarmos a opção Cauda inferior, vamos obter o menor número de ocorrências do desfecho, cuja probabilidade acumulada seja maior ou igual à probabilidade especificada no campo Probabilidades. Nesse exemplo, colocamos em Probabilidades o valor de probabilidade igual ao resultado obtido ao obtermos a probabilidade acumulada do número de ocorrências igual a 2, que é o resultado gerado a partir da configuração da figura 10.9. A saída do R é gerada pelo comando a seguir.

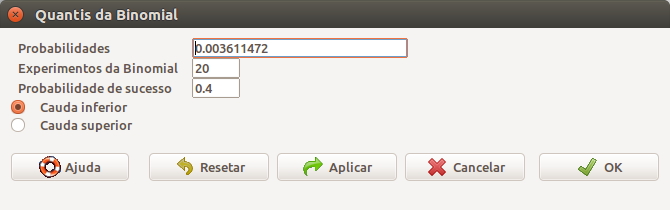
Figura 10.11: Diálogo do R Commander para obtermos os quantis da distribuição binomial. Ao selecionarmos a opção Cauda inferior, vamos obter o menor número de ocorrências do desfecho cuja probabilidade acumulada seja maior ou igual à probabilidade especificada no campo Probabilidades.

qbinom(c(0.003611472), size=20, prob=0.4, lower.tail=TRUE)

## [1] 2

De maneira análoga, ao especificarmos a Cauda superior, vamos obter o número mínimo de ocorrências do desfecho onde 1 - probabilidade acumulada seja menor ou igual à probabilidade especificada no campo Probabilidades. Por exemplo, especificando o valor 5.041261e-06 (figura 10.12), obtemos o valor 17, que corresponde ao primeiro valor especificado no campo Valores da variável na figura 10.10.

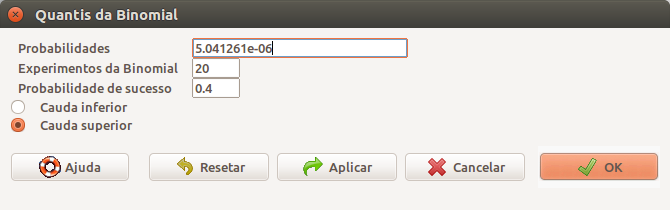
Figura 10.12: Diálogo do R Commander para obtermos os quantis da distribuição binomial. Ao selecionarmos a opção cauda superior, vamos obter o número mínimo de ocorrências do desfecho onde 1 - probabilidade acumulada seja menor ou igual à probabilidade especificada no campo Probabilidades.

qbinom(c(5.041261e-06), size=20, prob=0.4, lower.tail=FALSE)

## [1] 17

Vamos ver um outro exemplo. Suponhamos que queiramos obter o quantil da B(20, 0,4) para o qual a probabilidade de valores acima dele seja igual a 0,6 (Figura 10.13). O resultado é 7. Vejamos por que. As probabilidades da cauda superior para X = 6, 7 e 8 são respectivamente 0,750, 0,584 e 0,404. O valor X = 7 corresponde ao menor número de ocorrências k para o qual P(X > k) \(\le\) 0,6.

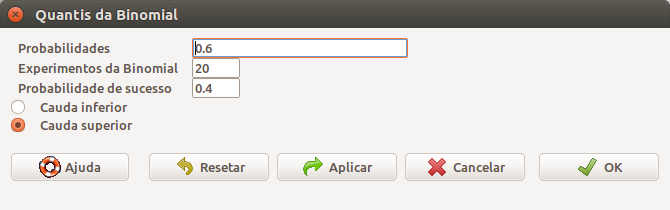
Figura 10.13: Diálogo do R Commander para obtermos o quantil da B(20, 0,4) para o qual 1 - probabilidade acumulada é igual a 0,6.

qbinom(c(0.6), size=20, prob=0.4, lower.tail=FALSE)

## [1] 7

Finalmente a última opção no menu da figura 10.1 pode ser usada para simular experimentos com a distribuição binomial. A partir da caixa de diálogo Sample from Binomial Distribution (figura 10.14), vamos simular um número de experimentos com uma distribuição binomial B(20, 0,4). Nessa figura, além dos parâmetros da binomial, também especificamos os seguintes parâmetros:

nome do conjunto de dados: BinomialSamples  
tamanho da amostra: 15  
número de observações: 10

Além disso, marcamos a opção Médias amostrais. Ao clicarmos em OK, serão geradas 15 linhas, cada linha contendo 10 possíveis números de ocorrências do desfecho em 20 experimentos, onde a probabilidade de ocorrência do evento em cada experimento é 0,4. Cada linha conterá também a média dos valores dos 10 números de ocorrências da linha. Os resultados serão armazenados no conjunto de dados BinomialSamples.

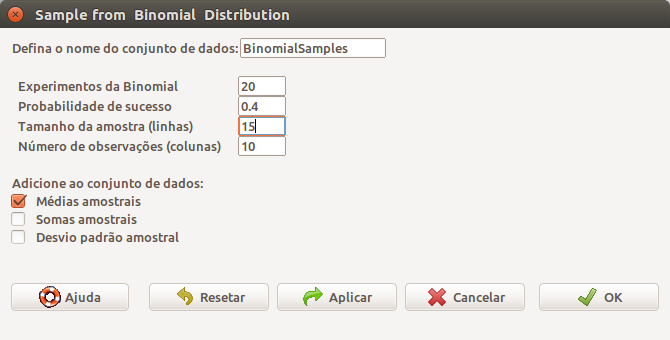
Figura 10.14: Diálogo do R Commander para gerar amostras de uma distribuição binomial.

Para observarmos as amostras geradas, clicamos no botão Ver conjunto de dados (figura 10.15), certificando-nos que o conjunto de dados BinomialSamples seja o conjunto ativo. Os dados gerados são mostrados na figura 10.16. Cada vez que gerarmos amostras da distribuição binomial, obteremos resultados diferentes.

Figura 10.15: Tela principal do R Commander. Visualizando o conjunto de dados BinomialSamples, obtido a partir da opção Sample from Binomial Distribution do menu da figura 10.1.

Observem que os números de ocorrência do desfecho mais frequentes estão na faixa entre 7 e 12, o que era de se esperar, já que as maiores probabilidades de ocorrência se situam nesta faixa (figura 10.3). Observem também que as médias do número de ocorrências em cada linha se situam entre 7,0 e 8,9. Isso também é de se esperar, conforme iremos ver na próxima seção.

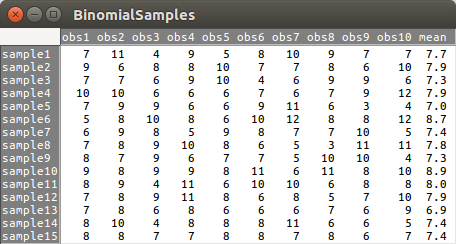
Figura 10.16: Amostras da distribuição binomial geradas a partir das opções estabelecidas na caixa de diálogo da figura 10.14.

Outro exemplo de uso da distribuição binomial: evidências anteriores indicaram que um dado componente eletrônico de um dispositivo biomédico tem a probabilidade 0,98 de funcionar satisfatoriamente. Ao comprar 5 desses componentes, deseja-se saber qual é a probabilidade de encontrarmos dois ou mais com defeito.

Entendendo como sucesso o evento componente sem defeito e considerando que temos 5 experimentos, então, para 2 ou mais equipamentos estarem com defeito, significa que, no máximo, 1 está funcionando corretamente, ou seja, desejamos \(P(X \le 1)\):

  \(P(X \le 1) = P(X = 0) + P(X = 1) = F(1)\)

Portanto podemos usar a fórmula (10.1) para calcularmos as probabilidades P(0) e P(1) e somarmos os dois valores, ou, usando o R Commander, na opção Probabilidades das caudas da binomial, preenchermos os campos conforme a figura 10.17 e obtemos o valor \(P(X \le 1) = 7,872\ .\ 10^{-7}\).

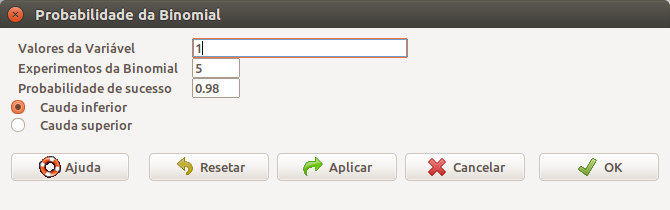
Figura 10.17: Diálogo do R Commander para obtermos a probabilidade acumulada da B(5, 0,98) para o número de ocorrências igual a 1.

10.2.2 Valor esperado e variância de uma distribuição binomial

10.2.2.1 Valor esperado

Para uma variável aleatória que segue uma distribuição binomial B(n,p), temos que o número esperado de sucessos é dado por np. Abaixo segue a demonstração desse resultado. O leitor pode saltar essa demonstração diretamente para a seção 10.2.2.2 sem perda de continuidade.

Usando a definição de valor esperado, podemos obter esse valor por aplicação da fórmula:

\(\begin{aligned} \ E[X] = \sum_{0}^{n}k.P(X=k)=\sum_{0}^{n}k.{n \choose k} p^{k} q^{n-k} \end{aligned}\)

Porém existe uma maneira mais fácil de calcular o E[X]. Para facilitar a solução desse problema e de outros, vamos introduzir aqui o uso de variáveis indicadoras. Para obtermos E[X], vamos definir n novas variáveis X_i , i=1, 2, 3, …, n:

\(\begin{aligned} X_i = \begin{cases} 1, \text{ se o i}_\text{ésimo}\text{ experimento for um sucesso}\\ 0, \text{ caso contrário} \end{cases} \end{aligned}\)

ou seja, para cada experimento, teremos uma indicação se ele foi um sucesso (1) ou um fracasso (0). Por exemplo, se n = 5, poderíamos ter como resultado SSFFS, ou seja, X = 3 sucessos, e os valores das variáveis indicadoras seriam X₁ = 1, X₂ = 1, X₃ = 0, X₄ = 0 e X₅ = 1. O número total de sucessos, X, é igual à soma das variáveis indicadoras, isto é:

\[\begin{align} \ X = X_1 + X_2 + X_3 + X_4 + X_5 = 3 \tag{10.2} \end{align}\]

Como o valor esperado de uma soma é igual à soma dos valores esperados, teríamos para n experimentos:

\(\begin{aligned} \ E[X] = E[X_1] + E[X_2] + \dots + E[X_n] \end{aligned}\)

O valor esperado para cada X_i para esse experimento é obtido assim:

\[\begin{align} E[X_i] &= 0\ .\ P(X_i = 0) + 1\ .\ P(X_i = 1) \\ &= P(X_i = 1) \\ &= p \tag{10.3} \end{align}\]

Teremos, então, para o valor esperado da binomial

\[\begin{align} E[X] &= p + p + ... + p \\ E[X] &= np \tag{10.4} \end{align}\]

10.2.2.2 Variância

A variância de uma distribuição binomial X ~ B(n, p) é dada por:

\[\begin{align} var(X) = np (1-p) = npq \tag{10.5} \end{align}\]

Demonstração: Para obtermos a variância da B(n,p) vamos usar uma propriedade da variância:

\(\begin{aligned} \ var(X) = E[X^2] - \mu^2 = E[X^2] - (E[X])^2 \end{aligned}\)

O E[X²] corresponde ao valor médio quadrático de uma variável aleatória. Voltando ao nosso problema de estimar a variância da B(n,p), usamos o resultado da seção anterior com a variável indicadora (equação (10.2)) para escrever

\(\begin{aligned} \ var(X) = var(X_1) + var(X_2) + ... + var(X_n) \end{aligned}\)

Para obtermos var(X_i), usamos a propriedade que acabamos de apresentar. Como X_i assume apenas os valores 0 ou 1, X_i² = X_i e, usando o resultado (10.3), temos que:

\(\begin{aligned} \ E[X_i^2]=E[X_i]=p \end{aligned}\)

Logo:

\(\begin{aligned} &\ var(X_i) = E[X_i^2] -(E[X_i])^2 = p - p^2 \\ &\ var(X_i) = p(1-p) \end{aligned}\)

Finalmente, como a var(X) para a binomial é simplesmente a soma de n variáveis indicadoras independentes, teremos:

\(var(X) = np (1-p) = npq\)

Para a distribuição B(20, 0,4), teremos:

E[X] = 0,4 x 20 = 8
var(X) = 20 x 0,4 x (1-0,4) = 4,8

Esses valores são compatíveis com as amostras da B(20, 0,4), mostradas na figura 10.16.

10.3 Distribuição de Poisson

Os conteúdos desta seção e da subseção 10.3.1 podem ser visualizados neste vídeo.

Outra distribuição de probabilidades de uma variável aleatória discreta bastante utilizada é a distribuição de Poisson, descrita por:

\[\begin{align} P(X=k) = Pois(\lambda) = \frac{e^{-\lambda}\lambda^k}{k!} \tag{10.6} \end{align}\]

onde \(\lambda\) é o número médio de eventos em um dado intervalo de tempo (ou outra unidade, por exemplo de distância, ou área). O modelo de Poisson é bastante utilizado para estudos de fila, ocorrência de doenças raras, falhas de equipamentos, etc. Por exemplo, poderíamos ter que o número médio de cirurgias por dia em um certo hospital é de 10, logo \(\lambda\)=10. Com base no modelo de Poisson, teríamos como obter as probabilidades de termos k=0,1,2,3,… cirurgias em um dia. Assim, por exemplo, a probabilidade de ocorrer 8 cirurgias em um dia é dada por:

\(\begin{aligned} P(X=8) = Pois(\lambda) = \frac{e^{-10}10^8}{8!}=0,1126 \end{aligned}\)

Podemos usar o R Commander para obter as probabilidades de uma distribuição de Poisson, traçar gráficos, obter os quantis da distribuição, bem como as probabilidades das caudas de uma distribuição de Poisson, de maneira análoga aos procedimentos mostrados na seção sobre a distribuição binomial. Assim, por exemplo, a figura 10.18 mostra como acessar as diversas opções disponíveis para a distribuição de Poisson no R Commander. Uma diferença em relação à distribuição binomial é que, para a distribuição de Poisson, somente devemos especificar um parâmetro, a média, que é igual a \(\lambda\). Na figura 10.19, especificamos o valor de \(\lambda\) igual a 10 para obtermos as probabilidades da distribuição de Poisson do exemplo acima.

Figura 10.18: Acessando o menu do R Commander que nos permite trabalhar com a distribuição de Poisson.

Figura 10.19: Diálogo do R Commander, onde especificamos o parâmetro da distribuição de Poisson. A seguir, clicamos em OK para obtermos as probabilidades.

A figura 10.20 mostra as probabilidades para a distribuição de Poisson para \(\lambda\) = 10 e para o número de ocorrências variando de 2 a 22. Observem que P(X=8) = 0,112599, coincidindo com o valor calculado pela fórmula (10.6).

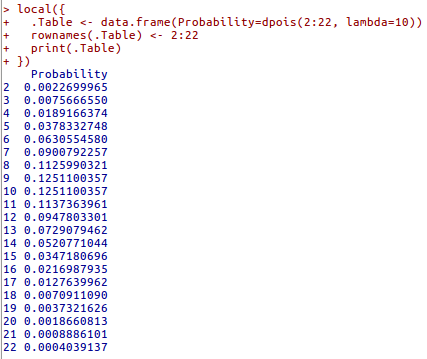
Figura 10.20: Probabilidades de ocorrência de 2, 3,…, 22 cirurgias em um dia, supondo que o número de cirurgias segue a distribuição Pois(10).

A figura 10.21 mostra o gráfico da distribuição de probabilidades para uma variável aleatória que segue a distribuição de Poisson com \(\lambda\) = 10. Observem que os valores da variável aleatória X podem variar de 0 até \(\infty\). Porém, para \(\lambda\) = 10, as probabilidades para X > 22 são desprezíveis.

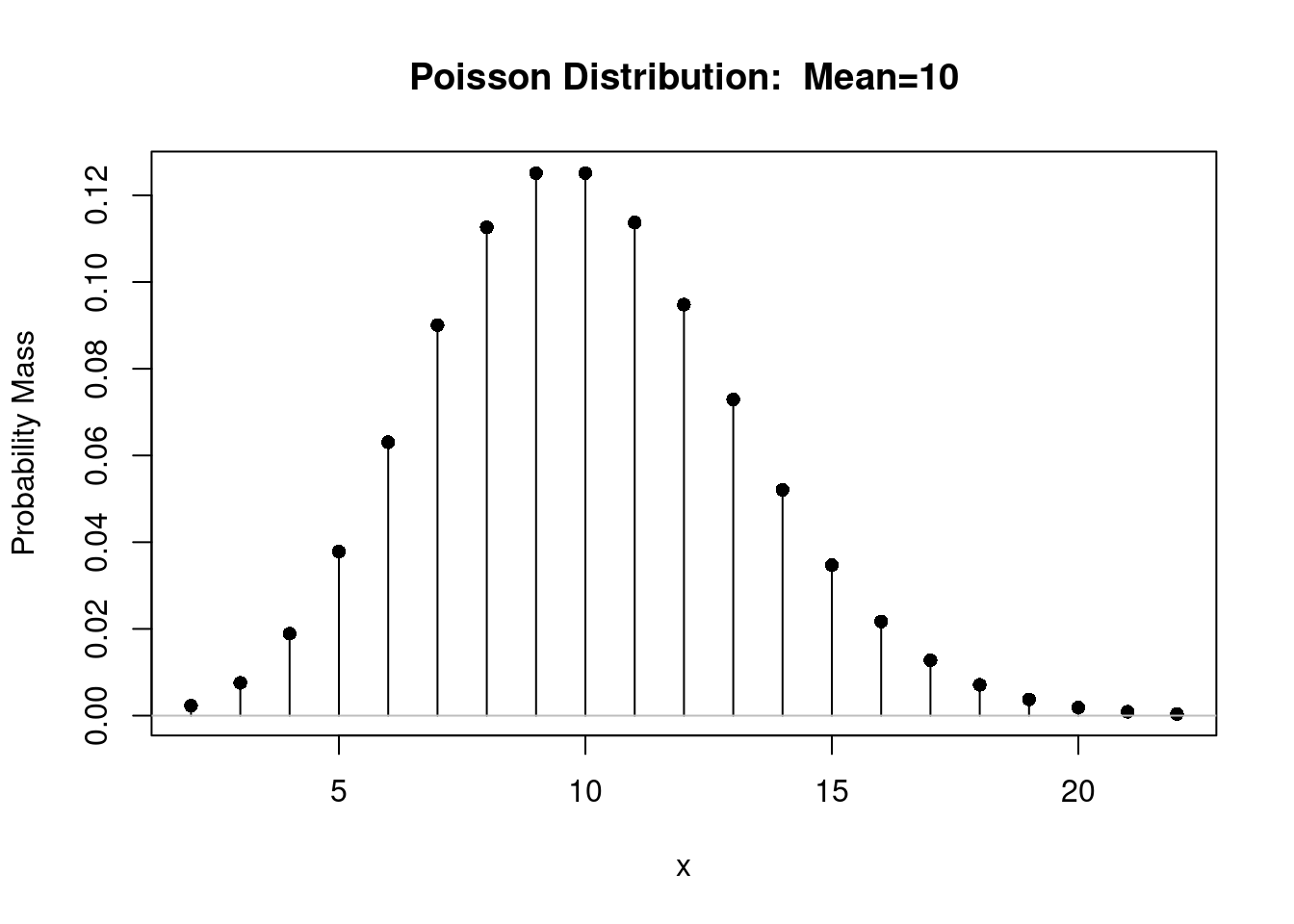
Figura 10.21: Gráfico da distribuição de Poisson para \(\lambda\) = 10.

A figura 10.22 mostra os gráficos das funções distribuição de probabilidades para variáveis aleatórias que seguem a distribuição de Poisson para \(\lambda\) = 0,5; 1,0; 1,5; e 3, respectivamente.

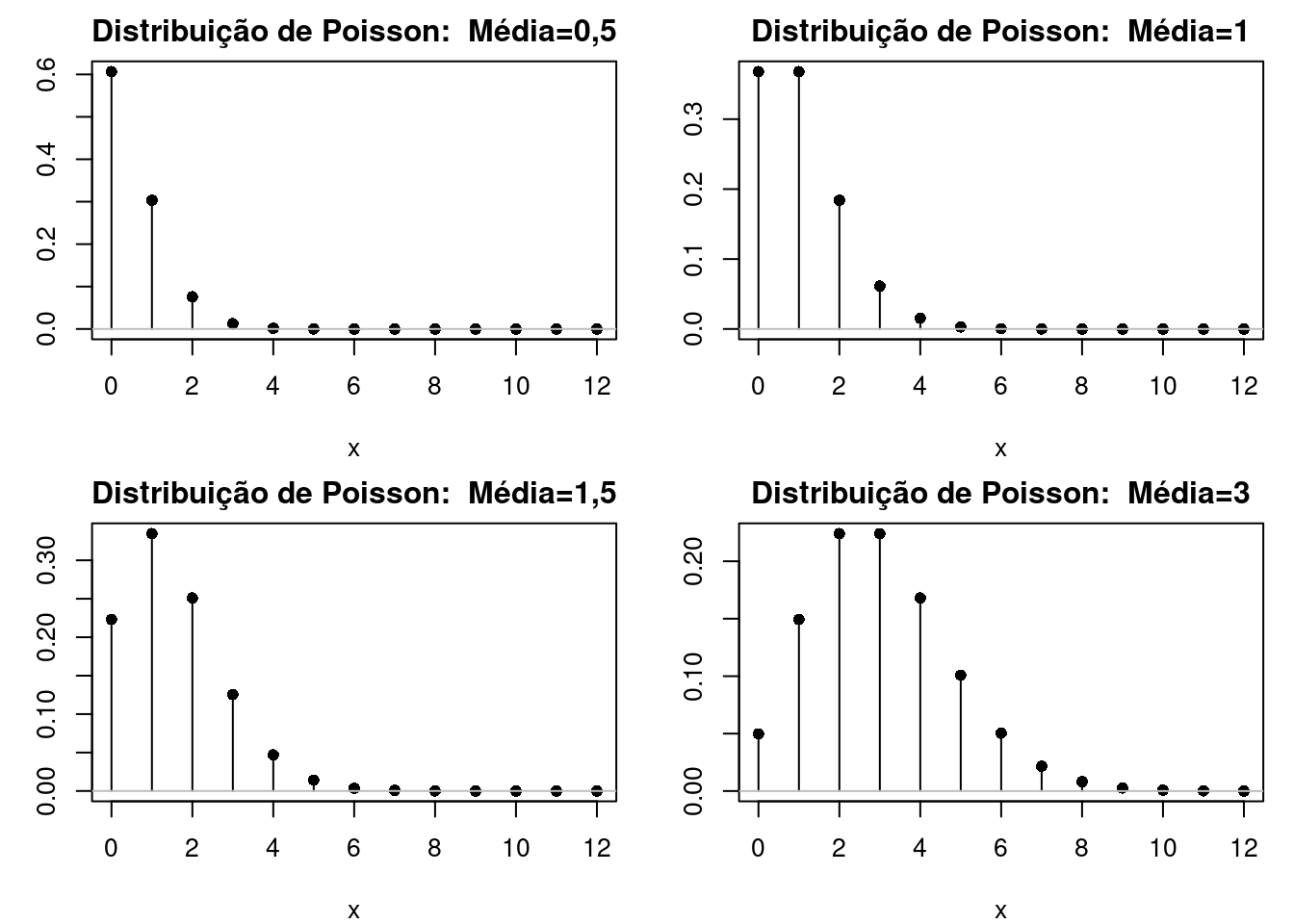
Figura 10.22: Gráficos da distribuição de probabilidades de Poisson para \(\lambda\) = 0,5; 1,0; 1,5; e 3, respectivamente.

O modelo de Poisson pode ser entendido como a ocorrência aleatória de eventos ao longo do tempo ou do espaço uni, bi ou tridimensional. A figura 10.23 mostra a situação onde x denota um evento ocorrendo aleatoriamente ao longo do tempo.

Figura 10.23: Eventos ocorrendo aleatoriamente ao longo do tempo.

Assumindo que ocorram \(\mu\) eventos em média em um intervalo de tempo unitário, então, em um intervalo de tempo t, teremos \(\mu\)t eventos em média. Supondo que a distribuição de Poisson se aplique a esse caso, então, para calcular as probabilidades de ocorrência de um certo número de eventos no intervalo de tempo t, utiliza-se a fórmula (10.6) com o parâmetro \(\lambda\) substituído por \(\mu\)t. No exemplo da cirurgia, sabemos que, em média, ocorrem 10 cirurgias por dia. Se desejássemos a distribuição de probabilidades para o número de cirurgias por semana, então utilizaríamos \(\lambda\) = 10 x 7 = 70. Caso desejássemos a distribuição de probabilidades para o número de cirurgias em 20 dias, então utilizaríamos \(\lambda\) = 10 x 30 = 300.

Exemplo: O número de partículas que atingem um dado dispositivo de medida em 40 períodos consecutivos de um minuto é dado na tabela 10.1 (colunas 1 e 2). Assumindo que as partículas atingem o dispositivo aleatoriamente com uma taxa média constante, podemos assumir como um modelo adequado a distribuição de Poisson para descrever as frequências observadas. Para verificarmos esse modelo, podemos, a partir dos dados, calcular a taxa média por unidade de tempo (minuto), obter as probabilidades de Poisson e, a seguir, calcular a frequência esperada do número de partículas em cada minuto.

Tabela 10.1: Número de partículas que atingem um dado dispositivo por minuto.

No. Partículas (k)	No. períodos com k partículas (Frequência Observada)	Probabilidades de Poisson	Frequência Esperada
0	13	0,301	12,04
1	13	0,361	14,44
2	8	0,217	8,68
3	5	0,087	3,48
4	1	0,026	1,04
5+	0	0,008	0,32
Total	40

Com base nos dados da tabela 10.1, o número total de partículas observadas em 40 minutos é

13 + (2 x 8) + (3 x 5) + (4 x 1) = 48

Para o modelo de Poisson, estimamos que a taxa média por unidade de tempo (minuto) é dada por \(\lambda\) = 48/40 = 1,2. Logo a distribuição de Poisson é dada por:

\(\begin{aligned} Pois(\lambda=1,2) = \frac{e^{-1,2}1,2^k}{k!}, \ k\ =\ 1,\ 2,\ \dots \end{aligned}\)

Usando o R, podemos calcular as probabilidades para k = 0, 1, 2, … e, a seguir, multiplicando-as por 40, obtemos as frequências esperadas para comparar com as observadas (quarta coluna da tabela 10.1). Nesse exemplo, vemos que as frequências observadas são próximas das frequências esperadas de acordo com o modelo de Poisson.

10.3.1 Valor esperado e variância de uma distribuição de Poisson

O valor esperado e a variância de uma variável aleatória que possui uma distribuição de Poisson são iguais a \(\lambda\). A demonstração segue abaixo:

O valor esperado é dado por:

\(E[X] =\sum_{k=0}^{\infty}kP(X=k)=\sum_{k=0}^{\infty}k\frac{e^{-\lambda}\lambda^k}{k!}\)

\(\ \ \ \ \ \ \ \ =e^{-\lambda}(\frac{\lambda}{1!}+\frac{2\lambda^2}{2!}+\frac{3\lambda^3}{3!}+\dots)\)

\(\ \ \ \ \ \ \ \ =e^{-\lambda}\lambda(1+\lambda+\frac{\lambda^2}{2!}+\frac{\lambda^3}{3!}+\dots)\)

\(\ \ \ \ \ \ \ \ =e^{-\lambda}\lambda e^\lambda\)

\(\ \ \ \ \ \ \ \ =\lambda\)

Para determinarmos a variância, vamos primeiramente obter E[X²].

\(E[X^2] =\sum_{k=0}^{\infty}k^2P(X=k)=\sum_{k=0}^{\infty}k^2\frac{e^{-\lambda}\lambda^k}{k!}\)

\(\ \ \ \ \ \ \ \ \ =\sum_{k=1}^{\infty}k\frac{e^{-\lambda}\lambda^k}{(k-1)!}\)

Fazendo k = s + 1:

\(E[X^2] =\sum_{s=0}^{\infty}(s+1)\frac{e^{-\lambda}\lambda^{s+1}}{s!}\)

\(\ \ \ \ \ \ \ \ \ =\lambda\sum_{s=0}^{\infty}s\frac{e^{-\lambda}\lambda^s}{s!}+\lambda\sum_{s=0}^{\infty}1\frac{e^{-\lambda}\lambda^s}{s!}\)

\(\ \ \ \ \ \ \ \ \ =\lambda^2+\lambda\)

e a variância dessa variável aleatória é dada por:

\(var(X) = E[X^2] - (E[X])^2\)

\(\ \ \ \ \ \ \ \ \ = \lambda^2 + \lambda - \lambda^2\)

\(\ \ \ \ \ \ \ \ \ = \lambda\)

10.3.2 Aproximação da distribuição binomial pela de Poisson

A distribuição binomial pode ser aproximada pela de Poisson quando os parâmetros n tende a infinito e p tende a zero. Existe uma demonstração formal para essa propriedade (Höel 1971). Podemos ver que quando p → 0, q = 1 - p → 1. Logo o valor esperado e a variância da distribuição binomial serão iguais, como pode ser visto abaixo:

E[X] = np e var(X) = npq = np

Para n = 100 e p = 0,05, a figura 10.24, mostra as probabilidades da binomial B(100; 0,05) e de Pois(5) para valores de k=0,1,2, … ,14. Observem que os valores de probabilidades são bastante próximos, especialmente  para  valores  de  k < 11.  Assim  é razoável adotar a  política  de  que,  para  n \(\ge\) 100  e  p \(\le\) 0,05, a distribuição binomial pode ser aproximada pela distribuição de Poisson, com parâmetro igual ao valor esperado da distribuição binomial (Höel 1971).

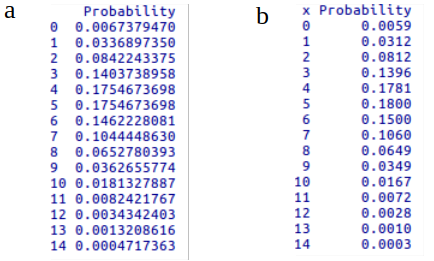
Figura 10.24: a) probabilidades para a distribuição B(100; 0,05); b) probabilidades para a distribuição Pois(5), mostradas somente para valores abaixo de 15.

10.4 Distribuição geométrica

Consideremos a seguinte situação. A probabilidade de sucesso em uma cirurgia é 0,20 e é constante de cirurgia para cirurgia, ou seja, não há melhoria dos resultados à medida que mais cirurgias são realizadas. Qual será o número médio de cirurgias que terão que ser realizadas até ocorrer o primeiro sucesso.

Essa situação é parecida com a distribuição binomial, porém com a seguinte diferença: nós não estamos interessados no número de sucessos em um certo número de experimentos (no caso cirurgias realizadas), mas sim em quantos experimentos precisam ser realizados até obtermos o primeiro sucesso. Se chamarmos de X a variável número de cirurgias até conseguirmos o primeiro sucesso, a distribuição de probabilidades de X é chamada de distribuição geométrica.

A distribuição geométrica se aplica quando se deseja saber o número de experimentos até a obtenção de um desfecho de interesse e quando as seguintes condições são satisfeitas:
1. Cada experimento é independente;
2. Cada experimento possui dois possíveis desfechos (sucesso ou fracasso);
3. A probabilidade de sucesso p é a mesma em cada experimento.

Representamos uma distribuição geométrica, que depende de um parâmetro p (probabilidade de sucesso em um experimento) por Geo(p).

10.4.1 Probabilidades de uma distribuição geométrica

Dada uma variável aleatória X, com distribuição Geo(p), como calculamos as probabilidades de serem realizados 1, 2, …, k experimentos até a obtenção do primeiro sucesso? A figura 10.25 nos auxilia no estabelecimento de uma fórmula geral para o cálculo dessas probabilidades.

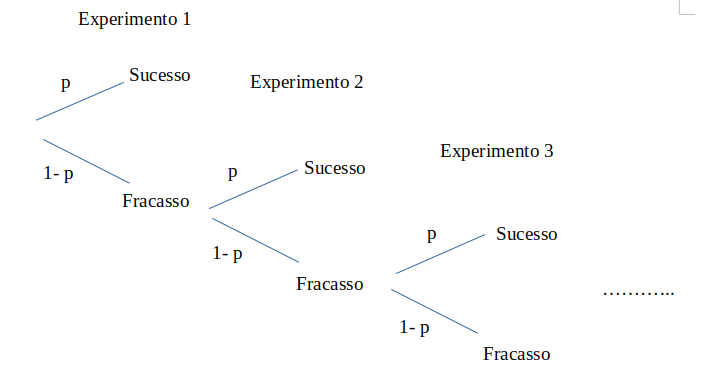
Figura 10.25: Árvore para a obtenção das probabilidades de uma distribuição geométrica com parâmetro p.

Vamos considerar cada valor da variável aleatória X. Quando X = 1, ou seja, sucesso no primeiro experimento, a probabilidade de sucesso no primeiro experimento é p. Logo:

\(\begin{aligned} P(X=1) = p \end{aligned}\)

Para termos o primeiro sucesso no segundo experimento, é necessário que o primeiro seja um fracasso e o segundo um sucesso. Então:

\(\begin{aligned} P(X=2) = (1-p)p \end{aligned}\)

Para termos um sucesso no terceiro experimento, é necessário que os dois primeiros experimentos sejam um fracasso e o terceiro um sucesso. Então:

\(\begin{aligned} P(X=3) = (1-p) (1-p) p = (1-p)^2 p \end{aligned}\)

Continuando com esse raciocínio, para o primeiro sucesso ocorrer no k-ésimo experimento, é necessário que os experimentos de 1 até k - 1 sejam fracassos. Logo:

\[\begin{align} P(X=k) = (1-p)^{k-1} p \tag{10.7} \end{align}\]

De modo análogo às distribuições binomial e de Poisson, podemos usar o R Commander para obtermos as probabilidades, gráficos, quantis, amostras e probabilidades da cauda de uma distribuição geométrica. A figura 10.26 mostra o gráfico da distribuição de probabilidades da distribuição geométrica com p = 0,2.

ATENÇÃO: observem que o gráfico começa a partir de 0 e que a variável aleatória é o número de fracassos até obter o primeiro sucesso. Assim as probabilidades mostradas no gráfico para X = k correspondem às probabilidades obtidas da fórmula (10.7) para X=k+1. Tenha isto sempre em mente quando usar o R Commander para trabalhar com a distribuição geométrica.

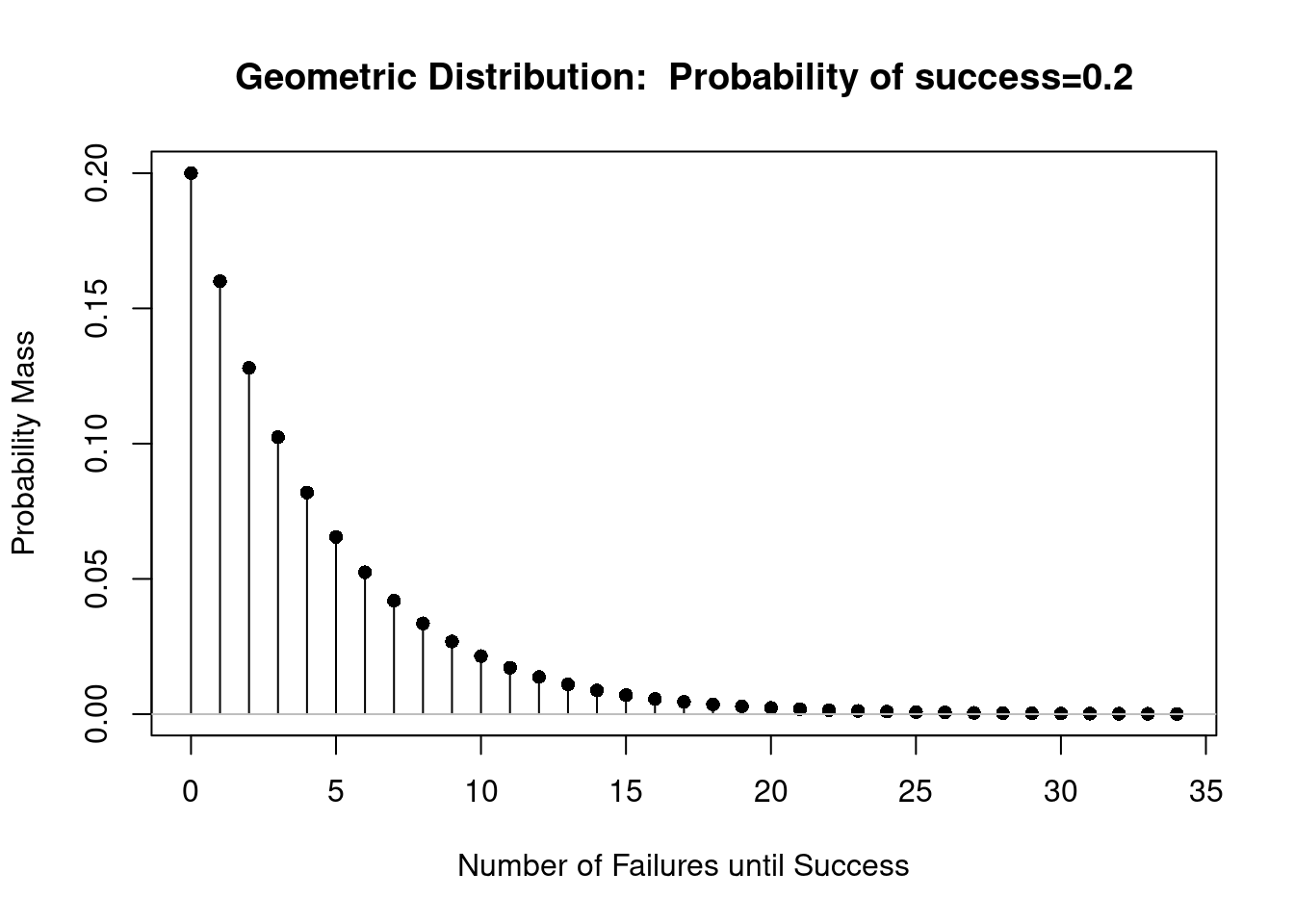
Figura 10.26: Distribuição de probabilidades para a distribuição Geo(0,2).

10.4.2 Valor esperado e variância de uma distribuição geométrica

O valor esperado de uma variável aleatória X com distribuição geométrica com parâmetro p é obtido a partir da aplicação da expressão de definição do valor esperado.

Pode-se demonstrar (vide (Meyer 1969)) que o valor esperado é dado por:

\[\begin{align} E[X] = 1/p \tag{10.8} \end{align}\]

Também não é difícil demonstrar que a variância de uma variável aleatória X com distribuição geométrica com parâmetro p é dada por:

\[\begin{align} var(X) = (1-p)/p^2 \tag{10.9} \end{align}\]

Voltando ao exemplo inicial, como a probabilidade de sucesso em uma cirurgia é de 0,20, então o valor esperado do número de cirurgias que precisam ser realizadas até se obter o primeiro sucesso é de 1/0,2 = 5.

10.5 Exercícios

1. Um cirurgião plástico quer comparar o número de enxertos de pele bem sucedidos em sua casuística de pacientes queimados com o número de outros pacientes queimados. Uma pesquisa na literatura indica que aproximadamente 30% dos enxertos infectam, porém que 80% sobrevivem.

   1. Qual a probabilidade de ocorrer 1 infecção em 8 pacientes?
   2. Qual a probabilidade de sobrevida de 7 dentre 8 enxertos?

2. Estime a probabilidade de um paciente cirúrgico apresentar 5 ou mais hospitalizações nos 10 anos de acompanhamento descritos em um estudo onde, nesse período, 390 pacientes cirúrgicos tiveram um total de 1487 hospitalizações.

3. O número de reações gastrointestinais relatadas de um certo medicamento anti-inflamatório foi de 538 por 9.160.000 prescrições. Isso corresponde a uma taxa de 0,58 reações gastrointestinais por 1000 prescrições. Usando o modelo de Poisson, encontre as probabilidades abaixo.

   1. Exatamente uma reação gastrointestinal em 1000 prescrições;
   2. Mais de 10 reações gastrointestinais em 1000 prescrições;
   3. Nenhuma reação gastrointestinal em 1000 prescrições.

Referências

Höel, Paul G. 1971. Introduction to Mathematical Statistics. 4th ed. John Wiley & Sons, Inc.

Meyer, Paul L. 1969. Introductory Probability and Statistical Applications. 2nd ed. Addison-Wesley Publishing Company, Inc.