15 Testes de hipóteses

15.1 Introdução

Este capítulo irá aprofundar diversos conceitos ligados aos testes de hipóteses, introduzidos no capítulo 6, enfatizando a importância do tamanho das amostras, o poder estatístico do teste e a intepretação correta dos valores de p.

15.2 Exemplo inicial (primeiro cenário)

Os conteúdos desta seção e da seção 15.3 podem ser visualizados neste vídeo.

Vamos iniciar com um exemplo. Supondo que a distribuição dos valores da glicemia de jejum em uma população de pessoas não diabéticas seja normal, um pesquisador deseja testar a hipótese de que a média de glicemia de jejum nessa população seja igual a 85 mg/dl. Como proceder?

Vamos considerar esse assunto, utilizando o que aprendemos de estatística até agora.

Sabemos que, se uma variável aleatória X possui uma distribuição normal com média \(\mu\), mas não sabemos a variância dessa distribuição, então a estatística:

\(\begin{aligned} T =\frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}} \end{aligned}\)

terá uma distribuição t de Student com n-1 graus de liberdade e

\(P\left[\mu - t_{n-1, 1-\alpha/2} \frac{S}{\sqrt{n}} \leq \bar{X} \leq \mu + t_{n-1, 1-\alpha/2}\frac{S}{\sqrt{n}}\right]=1-\alpha\)

ou seja, a probabilidade de extrairmos uma amostra de tamanho n dessa população e a média da amostra cair no intervalo a seguir é 1 – \(\alpha\):

\[\begin{align} \left[\mu - t_{n-1, 1-\alpha/2} \frac{S}{\sqrt{n}}, \mu + t_{n-1, 1-\alpha/2}\frac{S}{\sqrt{n}}\right] \tag{15.1} \end{align}\]

Então uma forma de testarmos a hipótese de que a média da população é de 85 mg/dl é adotar o seguinte enfoque: escolhemos um nível de confiança \((1 - \alpha)\), selecionamos uma amostra de um determinado tamanho da população, e verificamos se a média da amostra está fora do intervalo definido pela expressão (15.1). Se a média da amostra estiver fora do intervalo, a hipótese é rejeitada. Caso contrário, ela não é rejeitada.

Vamos aplicar esse raciocínio ao exemplo inicial. Vamos supor que o pesquisador selecionou o nível de confiança igual a 95%, ou seja, \(\alpha\) = 5%, e obteve na amostra de 36 pessoas uma média de 92 mg/dl e desvio padrão, s, igual a 16 mg/dl. Então, com 95% de probabilidade, o valor da média de uma amostra estaria no intervalo:

\[\begin{align} \left[85 - t_{35, 0,975} \frac{16}{\sqrt{36}}, 85 + t_{35, 0,975} \frac{16}{\sqrt{36}}\right]&= \left[85 - 2,03 \frac{16}{\sqrt{36}}, 85 + 2,03 \frac{16}{\sqrt{36}}\right] \\ &=\ [79,6-90,4]\ mg/dl \tag{15.2} \end{align}\]

O valor de \(t_{35, 0,975}\) acima pode ser obtido no R com o comando:

qt(.975, df=35)

## [1] 2.030108

O valor da média da amostra, 92 mg/dl, está fora do intervalo dado por (15.2). Portanto o pesquisador irá rejeitar a hipótese de que a média da glicemia de jejum nessa população seja de 85 mg/dl. A razão para essa rejeição é que, caso 85 mg/dl fosse a média de glicemia de jejum na população, a probabilidade de selecionar aleatoriamente uma amostra de 36 pacientes dessa população e a média cair fora do intervalo \([79,6 - 90,4]\) é de apenas 5%. Nesse caso, o pesquisador prefere acreditar que a média da população é diferente de 85 mg/dl.

Vamos a seguir abordar esse mesmo problema sob o ponto de vista de um teste de hipótese.

15.3 Processo para realizar um teste de hipótese

A forma exata como um teste de hipótese é conduzido depende de cada problema específico. Usando o exemplo anterior, vamos sistematizar os passos gerais para realizar um teste de hipótese, aproveitando para reforçar alguns conceitos e notações comumente utilizados e introduzidos no capítulo 6.

1) Passo 1: expressar o tema da pesquisa em termos de uma hipótese estatística

O primeiro passo é o de estabelecer uma hipótese que será avaliada. Essa hipótese é chamada de hipótese nula, representada por H₀. No exemplo anterior, a hipótese nula é de que a distribuição de probabilidades da glicemia de jejum na população que estamos estudando é normal com média igual a 85 mg/dl. Nada especificamos sobre o valor da variância. Ao estabelecermos uma hipótese a ser testada, a mesma será confrontada com uma hipótese alternativa, representada por H₁. No exemplo acima, a hipótese alternativa é que a distribuição de probabilidades da glicemia de jejum na população que estamos estudando é normal com média diferente de 85 mg/dl.

Assim temos:

H₀: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu = 85\ mg/dl\)

H₁: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu \ne 85\ mg/dl\)

2) Passo 2: decidir sobre um teste estatístico apropriado para testar a hipótese nula (escolha de uma estatística)

A partir da hipótese nula, podemos pensar em um teste estatístico apropriado para testá-la. No exemplo considerado, uma possibilidade é o de selecionarmos uma amostra aleatória da população com um certo número de elementos (n), calcularmos a média da amostra e compararmos com a média estabelecida pela hipótese nula.

Sabemos que a estatística

\[\begin{align} T =\frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}} \tag{15.3} \end{align}\]

terá uma distribuição t de Student com n-1 graus de liberdade, se a hipótese nula for verdadeira.

3) Passo 3: selecionar o nível de significância (\(\boldsymbol{\alpha}\)) para o teste estatístico

O nível de significância, também chamado de alfa, é um valor de probabilidade que o pesquisador considera suficientemente baixo que definirá uma região crítica da distribuição da estatística definida no passo 2, tal que, se o valor da estatística calculada a partir da amostra selecionada cair na região crítica, a hipótese nula será rejeitada. Caso contrário, a hipótese nula não será rejeitada. Escolhemos valores baixos para \(\alpha\), porque desejamos que seja baixa a probabilidade de rejeitarmos a hipótese nula quando ela for verdadeira. Valores tradicionais de \(\alpha\) são 0,1 (10%), 0,05 (5%) e 0,01 (1%), sendo o nível de 5% o mais frequentemente utilizado. Vamos tentar entender isso melhor.

Considerando que a estatística T, definida no passo 2, segue a distribuição t de Student, a figura 15.1 mostra o gráfico de T e dois pontos nessa distribuição \(-t_{n-1, 1-\alpha/2}\) e \(t_{n-1, 1-\alpha/2}\) que delimitam uma região (em vermelho) cuja área é igual a \(\alpha\) (a probabilidade de se obter um valor de t abaixo de \(-t_{n-1, 1-\alpha/2}\) ou acima de \(t_{n-1,1-\alpha/2}\)). Essa região é denominada de região crítica e os pontos \(-t_{n-1, 1-\alpha/2}\) e \(t_{n-1,1-\alpha/2}\) são chamados de pontos críticos.

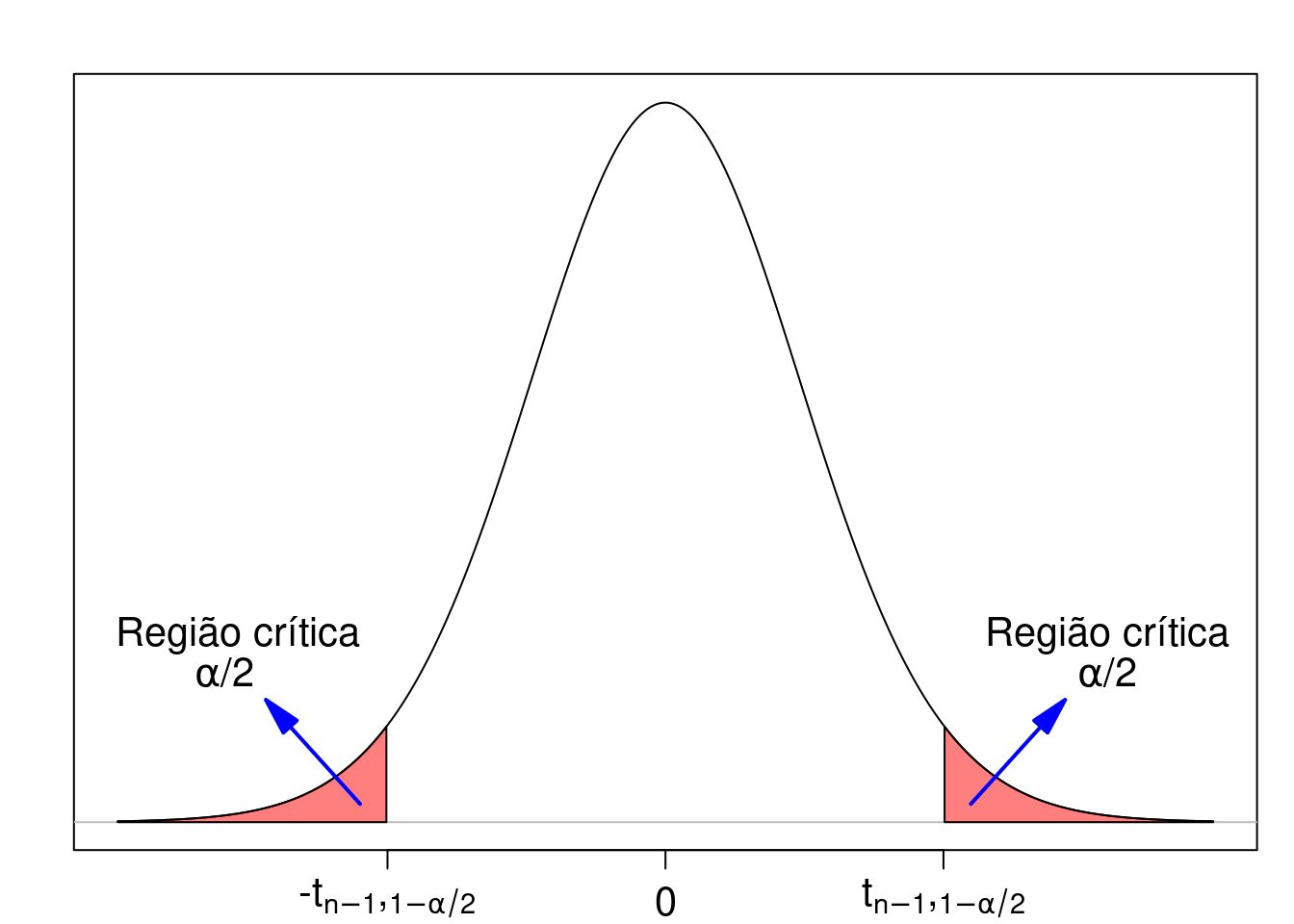
Figura 15.1: Definição da região crítica para o teste de hipótese definido no passo 2.

No exemplo acima, \(\alpha\) foi definido como 5% e n = 36. Assim o valor crítico \(t_{35,1-0,05/2} = t_{35; 0,975}\) é calculado no R da seguinte forma:

qt(.975, 35)

## [1] 2.030108

Então \(t_{35; 0,975}\) = 2,03.

4) Passo 4: selecionar a amostra e realizar os cálculos

Ao definirmos a estatística a ser utilizada, o valor de \(\alpha\) e, consequente, a região crítica do teste, procedemos à seleção da amostra do estudo, a partir da qual o valor da estatística será calculado e comparado com os valores críticos. Caso o valor da estatística caia dentro da região crítica do teste, a hipótese nula será rejeitada. Nesse caso, dizemos que o resultado do teste é estatisticamente significativo. Caso contrário, ela não será rejeitada e o resultado do teste não é estatisticamente significativo.

No exemplo considerado, a amostra da população gerou os seguintes resultados:
\(\bar{x}\) = 92 mg/dl
n = 36
s = 16 mg/dl

Substituindo esses valores na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{92-85}{\frac{16}{\sqrt{36}}}=2,62 \end{aligned}\)

5) Passo 5: tomar a decisão

A partir do cálculo do valor de t na amostra, vemos que \(t > t_{35; 0,975} = 2,03\). O valor de t caiu na região crítica e a hipótese nula é então rejeitada (figura 15.2). O resultado é estatisticamente significativo.

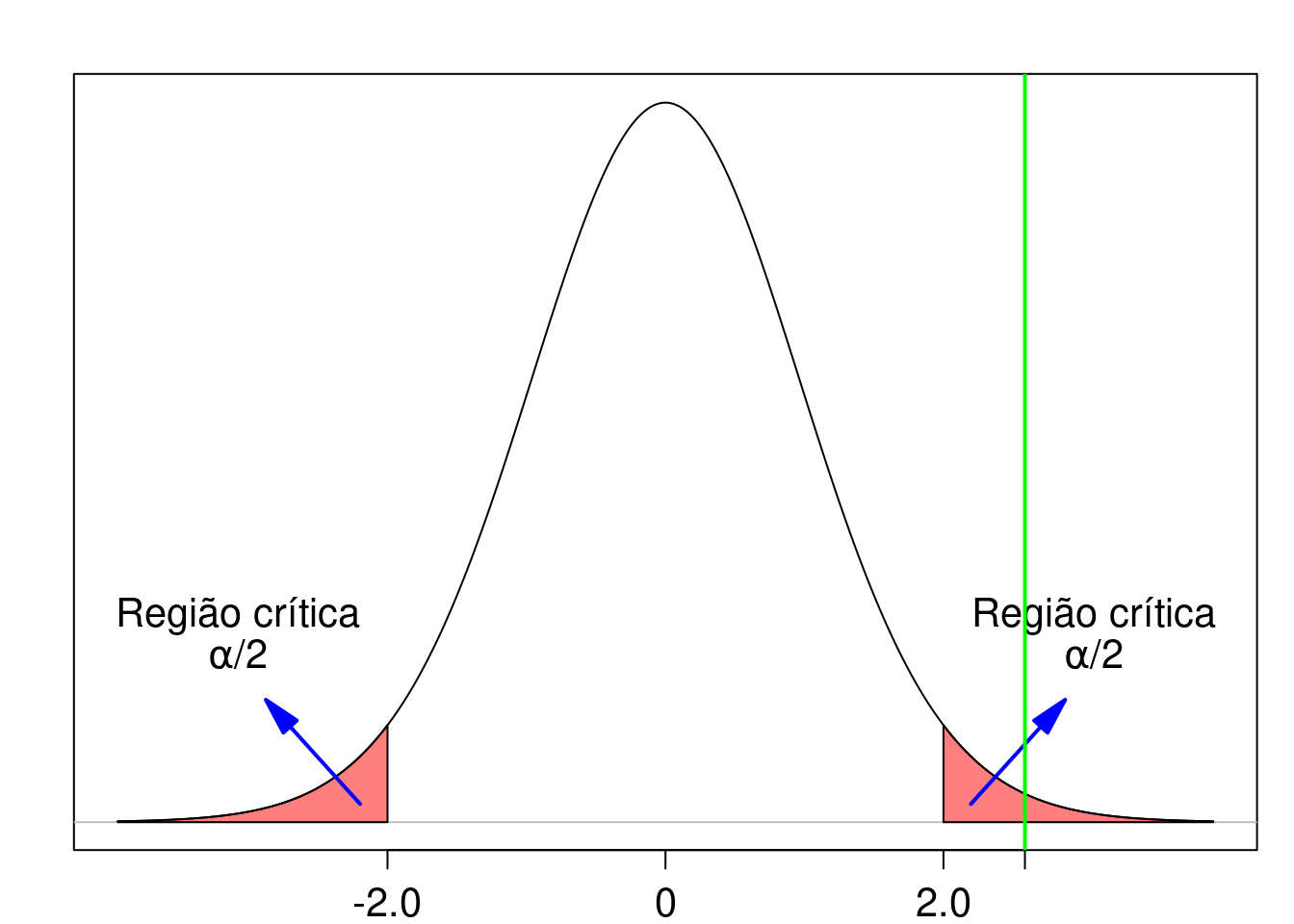
Figura 15.2: O valor da estatística no teste de hipótese é 2,62 (reta vertical verde) e está localizado na região crítica do teste. Portanto a hipótese nula é rejeitada.

15.3.1 Segundo cenário

Vamos supor que, ao extrairmos uma amostra aleatória da população no passo 4 da seção anterior, obtivéssemos os seguintes resultados:
\(\bar{x}\) = 89 mg/dl
n = 36
s = 16 mg/dl

Substituindo esses valores na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{89-85}{\frac{16}{\sqrt{36}}}=1,50 \end{aligned}\)

A partir do cálculo do valor de t nessa amostra, vemos que \(-t_{35; 0,975} \le t \le t_{35; 0,975}\). O valor de t não caiu na região crítica e a hipótese nula não é rejeitada (figura 15.3). O resultado não é estatisticamente significativo.

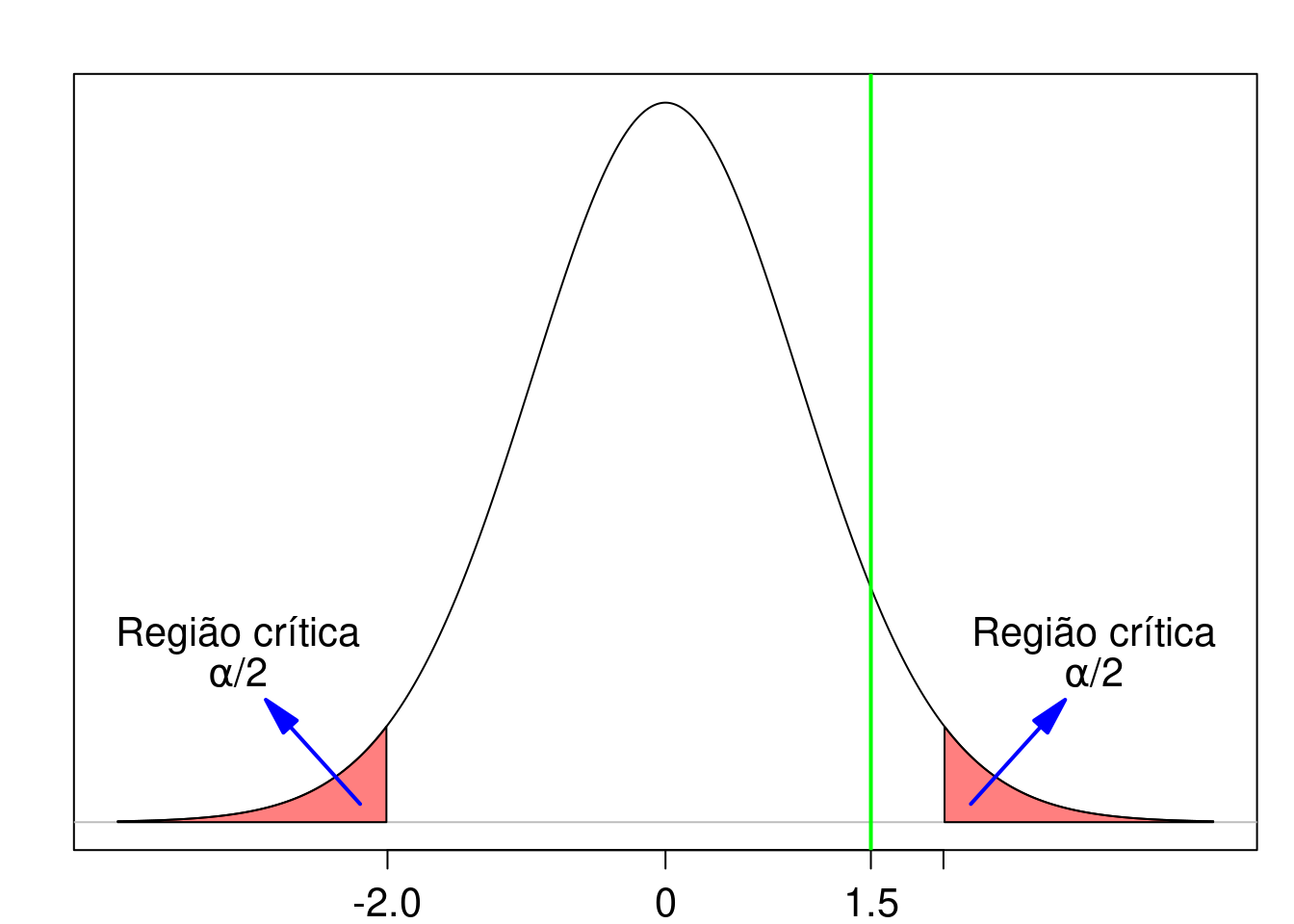
Figura 15.3: O valor da estatística no teste de hipótese é 1,50 (reta vertical verde) e está localizado fora da região crítica do teste. Portanto a hipótese nula não é rejeitada.

15.4 Relação entre o intervalo de confiança e o teste de hipótese

Os conteúdos desta seção e da seção 15.5 podem ser visualizados neste vídeo.

Também podemos, em muitas situações, usar o intervalo de confiança para decidir sobre a significância ou não de um resultado de um teste estatístico.

Retomando o exemplo da introdução, vamos novamente calcular o intervalo de confiança com nível de confiança de 95% (1 - \(\alpha\) = 0,95). Para uma variável aleatória X que segue uma distribuição normal com média \(\mu\) e variância desconhecida, o intervalo de confiança, obtido a partir de uma amostra de tamanho n, é dado pela expressão (14.9) do capítulo 14:

\(\begin{aligned} &\ \left[\bar{X} - t_{n-1, 1-\alpha/2} \frac{S}{\sqrt{n}}, \bar{X} + t_{n-1, 1-\alpha/2}\frac{S}{\sqrt{n}}\right] \end{aligned}\)

Substituindo os valores produzidos pela amostra:
\(\bar{x}\) = 92 mg/dl
n = 36
s = 16 mg/dl
\(t_{35; 0,975} = 2,03\)

na expressão acima, resulta no seguinte intervalo de confiança:

IC(95%): \(86,6 \le \mu \le 97,4\)

A linha horizontal em azul na figura 15.4 mostra o intervalo de confiança calculado acima. Para esse teste de hipótese, a hipótese nula foi rejeitada e o intervalo de confiança não contém o valor estabelecido pela hipótese nula (85 mg/dl).

Assim, se o intervalo de confiança não contiver o valor do parâmetro sob a hipótese nula que está sendo testada, então a hipótese nula será rejeitada.

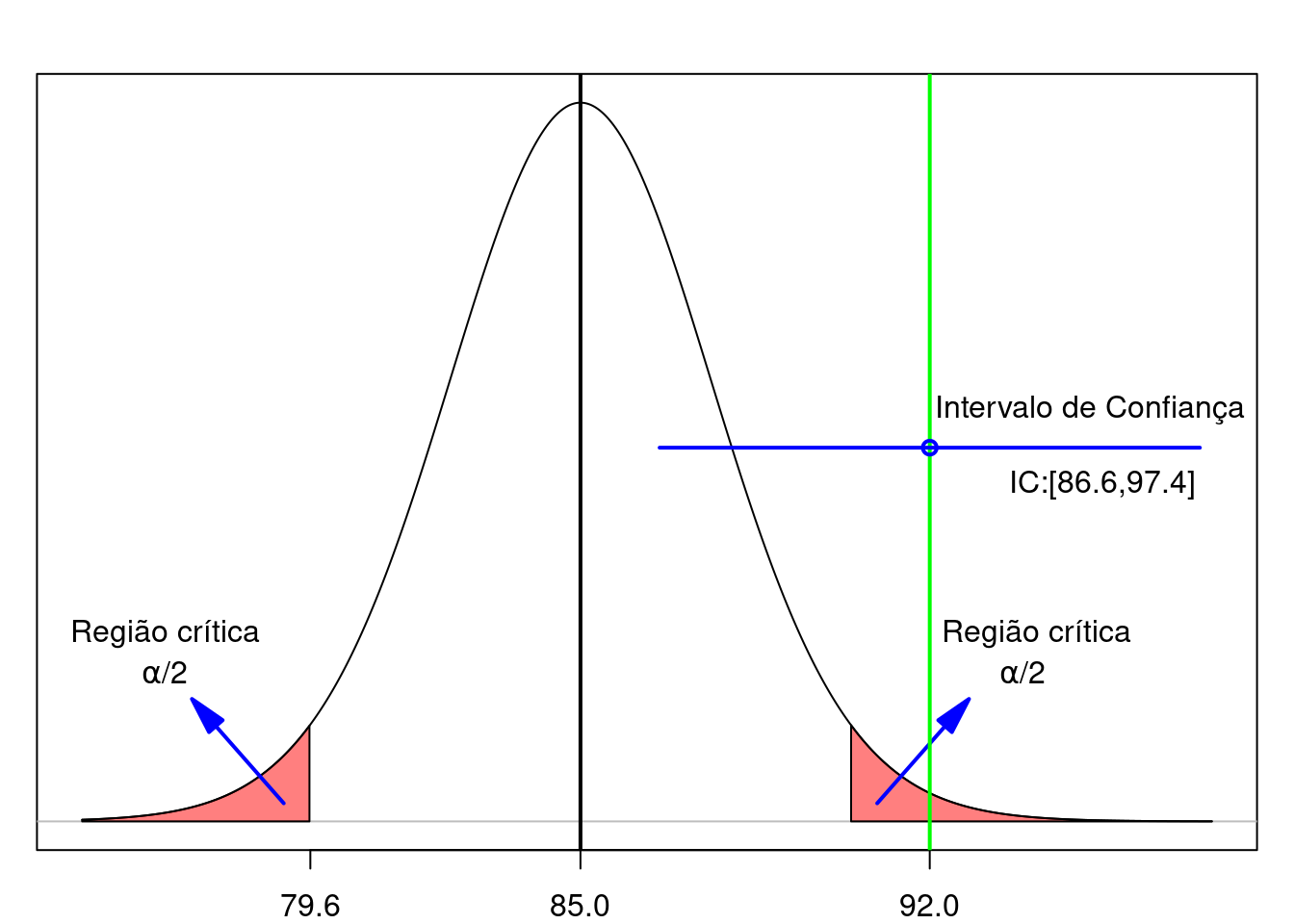
Figura 15.4: Relação entre um teste de hipótese e o intervalo de confiança quando a hipótese nula é rejeitada. A linha verde indica o valor da média amostral.

No outro cenário mostrado ao final da seção anterior, onde a amostra gerou os seguintes valores:
\(\bar{x}\) = 89 mg/dl
n = 36
s = 16 mg/dl

o intervalo de confiança será:

IC(95%): \(83,6 \le \mu \le 94,4\)

A linha horizontal em azul na figura 15.5 mostra o intervalo de confiança calculado acima. Para esse teste de hipótese, a hipótese nula não foi rejeitada e o intervalo de confiança contém o valor estabelecido pela hipótese nula (85 mg/dl).

Assim, se o intervalo de confiança incluir o valor do parâmetro sob a hipótese nula que está sendo testada, então ela não será rejeitada.

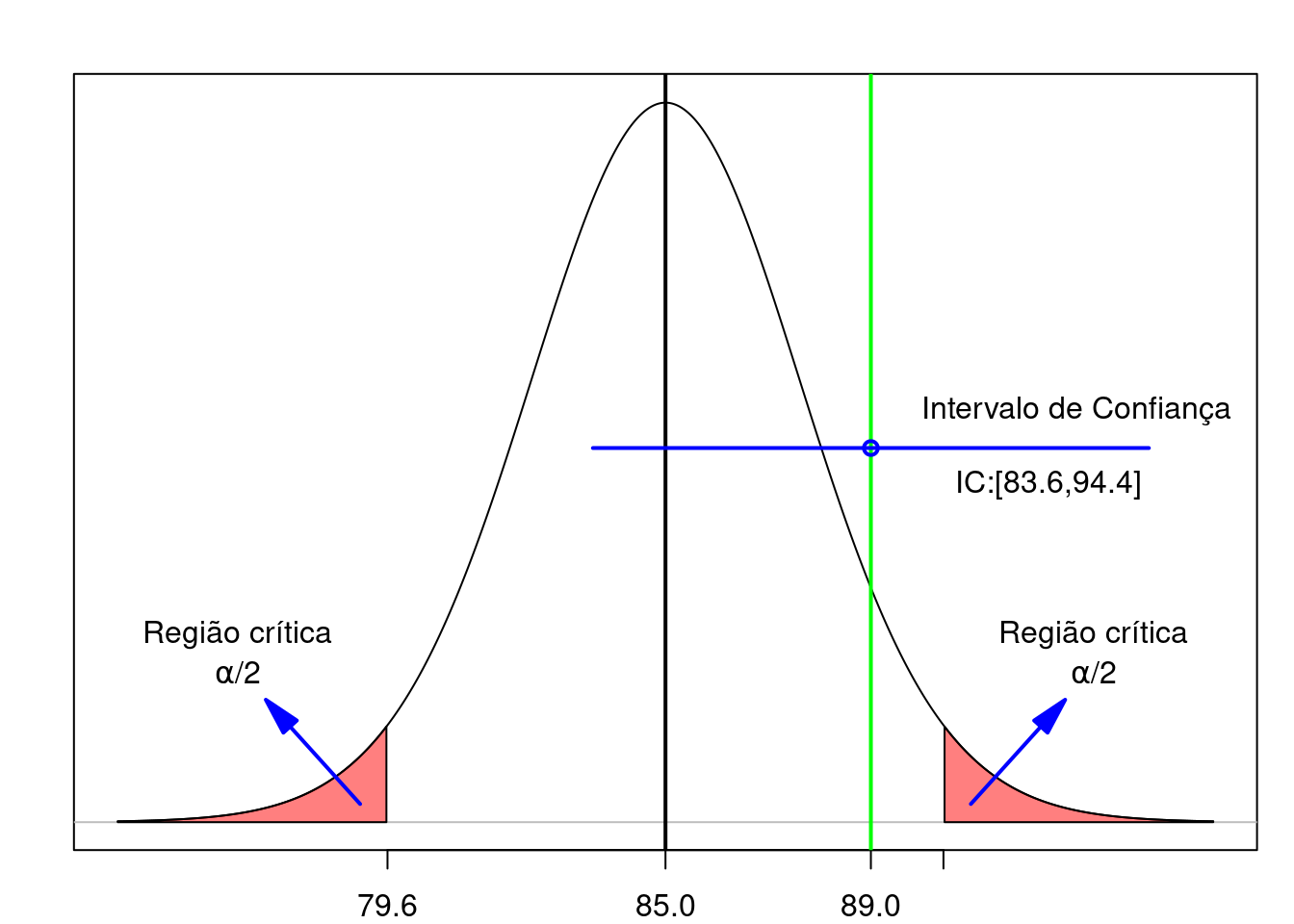
Figura 15.5: Relação entre um teste de hipótese e o intervalo de confiança quando a hipótese nula não é rejeitada. A linha verde indica o valor da média amostral.

Novamente vamos enfatizar que o intervalo de confiança fornece mais informações do que a simples rejeição ou não de uma hipótese nula. Ele também nos fornece a precisão da estimativa do parâmetro considerado, nos permitindo também avaliar a relevância clínica do achado (seção 6.10).

15.5 Interpretação alternativa para o IC

Os limites de um intervalo de confiança podem ser obtidos de maneira análoga à utilizada para obter o intervalo de confiança para a diferença de médias dos valores de ácido fólico para dois métodos diferentes de ventilação, conforme mostrado no capítulo 6, seção 6.5.

Vamos supor que estamos interessados em calcular o intervalo de confiança para a média de uma variável que segue uma distribuição normal com variância conhecida, \(\sigma\), e que calculamos a média amostral (\(\bar{x}\)) de uma amostra de tamanho n, extraída aleatoriamente da população com essa distribuição.

A figura 15.6 mostra uma maneira diferente de interpretar os limites superior e inferior do intervalo de confiança.

O limite inferior do intervalo de confiança, \(\mu_i\), pode ser obtido traçando o gráfico da distribuição normal da média amostral com variância igual a \(\sigma/\sqrt{n}\), de tal modo que a área sob essa distribuição acima de \(\bar{x}\) barra seja igual a \(\alpha/2\), que é igual à probabilidade de obtermos aleatoriamente uma amostra de tamanho n da população com média igual a \(\mu_i\) e a média amostral ser maior do que \(\bar{x}\). Para qualquer valor de média da distribuição normal abaixo de \(\mu_i\), a probabilidade de se obter uma média de uma amostra com tamanho n maior que a média amostral encontrada, \(\bar{x}\), será menor que \(\alpha/2\). Assim todas as hipóteses nulas cujos valores de médias fossem menores do que \(\mu_i\) seriam rejeitadas no teste de hipótese realizado a partir dessa amostra.

O limite superior do intervalo de confiança, \(\mu_s\), pode ser obtido traçando o gráfico da distribuição normal da média amostral com variância igual a \(\sigma/\sqrt{n}\), de tal modo que a área sob essa distribuição abaixo de \(\bar{x}\) seja igual a \(\alpha/2\), que é igual à probabilidade de obtermos aleatoriamente uma amostra de tamanho n da população com média igual a \(\mu_s\) e a média amostral ser menor do que \(\bar{x}\). Para qualquer valor de média da distribuição normal acima de \(\mu_s\), a probabilidade de se obter uma média de uma amostra com tamanho n menor que a média amostral encontrada, \(\bar{x}\), será menor que \(\alpha/2\). Assim todas as hipóteses nulas cujos valores de médias fossem maiores do que \(\mu_s\) seriam rejeitadas no teste de hipótese realizado a partir dessa amostra.

Logo o intervalo de confiança é dado por todos os valores de média, \(\mu\), tal que é \(\mu_i \le \mu \le \mu_s\). A distância de \(\bar{x}\) até \(\mu_i\) ou \(\mu_s\) é igual \(z_{1-\alpha/2} .\sigma/ \sqrt{n}\). Esse intervalo de confiança é o mesmo que obtivemos na seção 14.2, capítulo 14, e pode ser interpretado como o conjunto de valores de médias da distribuição normal correspondentes a hipóteses nulas que não seriam rejeitadas por um teste de hipótese realizado a partir dos dados obtidos na amostra do estudo.

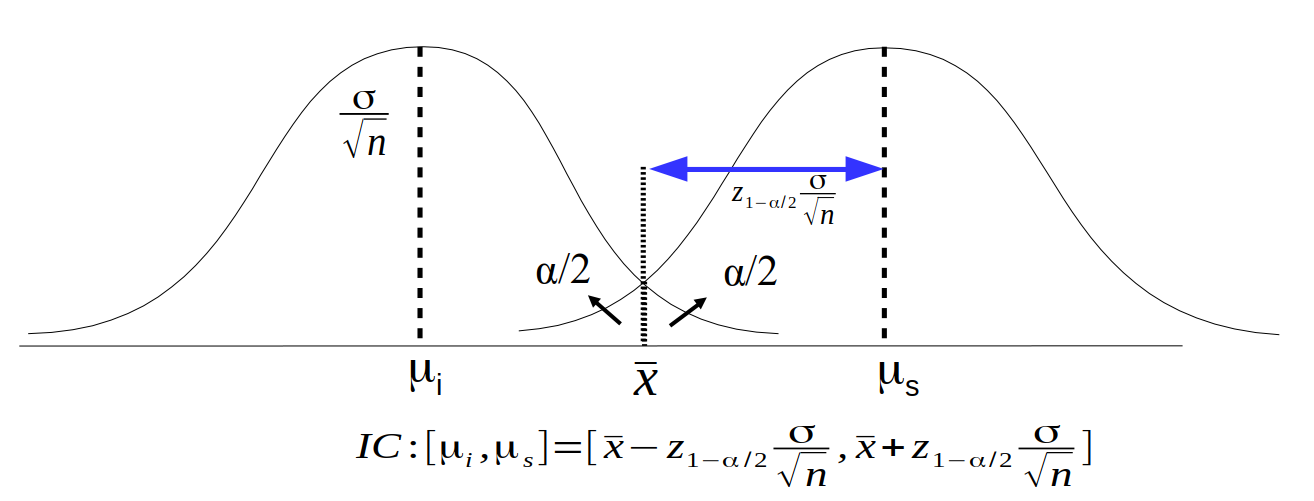
Figura 15.6: Interpretação alternativa dos limites do intervalo de confiança. Sendo \(\bar{x}\) a média amostral, \(\mu_i\) e \(\mu_s\) correspondem aos limites inferior e superior do intervalo de confiança para a média da população.

A aplicação Limites do intervalo de confiança distribuição normal (figura 15.7) permite ao usuário encontrar os limites do intervalo de confiança para a média de uma população com uma distribuição normal, com variância conhecida. Ao especificar o desvio padrão da população, o tamanho amostral, o nível de confiança e a média amostral, o usuário pode variar os valores do limite superior e limite inferior. O valor de alfa/2 corresponde à área em vermelho para cada um dos limites. Quando o valor de alfa/2 para o correspondente limite for igual a (1 – nível de confiança/100)/2, a área vermelha ficará verde e o valor do correspondente limite do intervalo de confiança será mostrado em azul na tela, como visto na figura 15.8. Experimente.

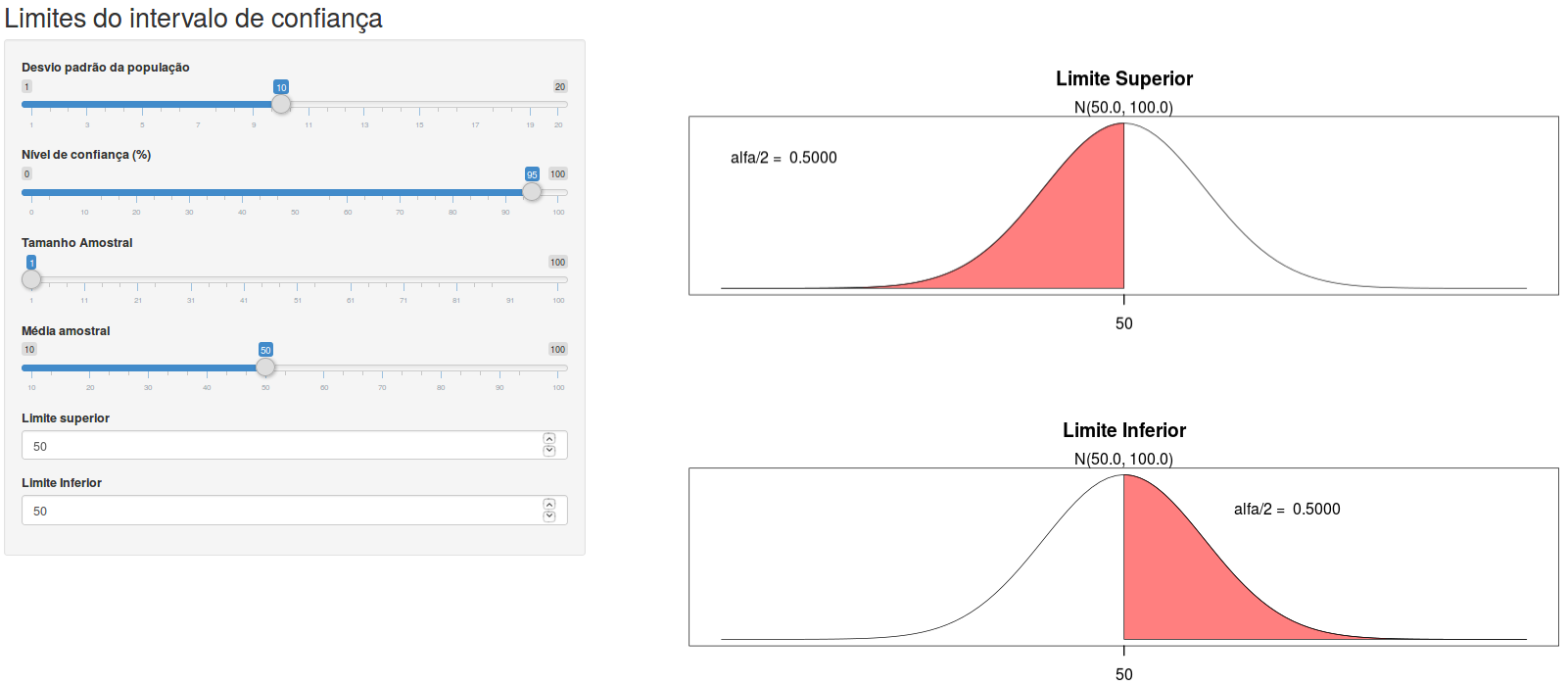
Figura 15.7: Aplicação que permite encontrar os limites do intervalo de confiança, manipulando os valores do limite superior e inferior à esquerda da tela, uma vez selecionados os valores do nível de confiança, desvio padrão da população, média amostral e tamanho da amostra.

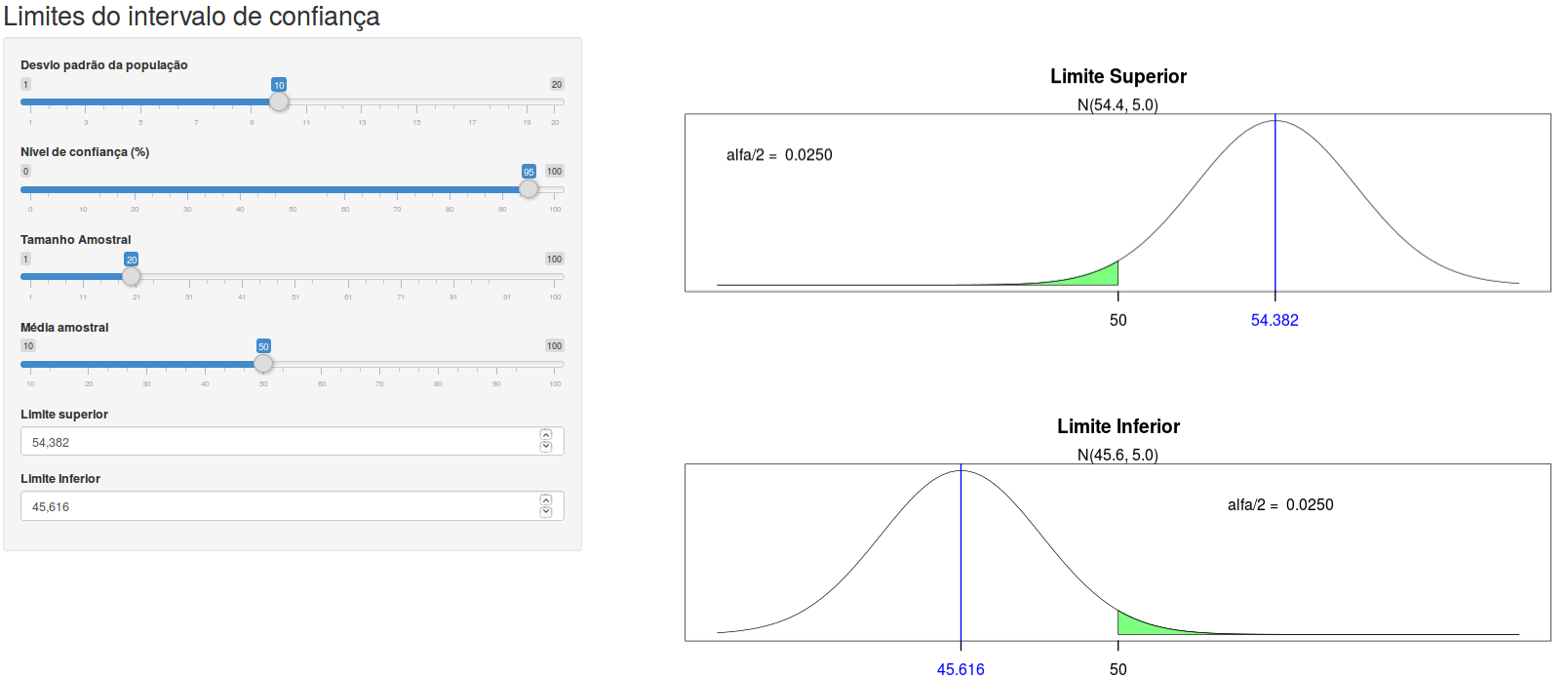
Figura 15.8: Usando a aplicação da figura 15.7, com o nível de confiança igual 95%, desvio padrão = 10, tamanho amostral = 20 e média amostral = 50, os limites do intervalo de confiança são limite inferior = 45,616 e limite superior = 54,382.

Essa interpretação alternativa para o intervalo de confiança fornece um método para o cálculo dos limites do intervalo para situações nas quais esses limites não são expressos por expressões analíticas como mostrado na seção seguinte.

15.6 IC para proporções em pequenas amostras

Para a proporção de sucessos em um experimento de Bernoulli, usamos na seção 14.7 uma aproximação pela normal. Conforme já vimos, essa é uma boa aproximação para um número grande de experimentos. Para amostras pequenas, ou mesmo para amostras grandes, podemos obter o intervalo de confiança exato por meio do cálculo de probabilidades de um modelo binomial.

Por exemplo, consideremos 8 experimentos de Bernoulli, sendo que o evento de interesse tenha ocorrido 6 vezes (\(\hat{p} = 0,75\)). Caso utilizássemos a aproximação para a normal para calcularmos o intervalo de confiança da proporção de sucessos (nível de 95%), obteríamos:

\(0,75 - 1,96 \sqrt{\frac{0,75(1-0,75)}{8}} \leq p \leq 0,75 + 1,96 \sqrt{\frac{0,75(1-0,75)}{8}}\)

\(0,4500 \leq p \leq 1,200\)

ou, usando a correção de continuidade: \(0,3875 \leq p \leq 1,2625\).

Obviamente, a probabilidade p não pode ser maior do que 1. O intervalo exato com nível de confiança \((1 - \alpha)\) pode ser obtido da seguinte forma:

1. o limite inferior do IC é obtido aplicando a distribuição binomial para 8 experimentos e experimentando com valores da probabilidade de sucesso até que a probabilidade de se observar um número de eventos maior ou igual a 6 seja \(\alpha/2\);

2. o limite superior do IC é obtido aplicando a distribuição binomial para 8 experimentos e experimentando com valores da probabilidade de ocorrência de sucesso até que a probabilidade de se observar um número de eventos menor ou igual a 6 seja \(\alpha/2\).

A aplicação Limites do intervalo de confiança distribuição binomial (figura 15.9) permite ao usuário encontrar os limites do intervalo de confiança para a probabilidade de uma distribuição binomial. Ao especificar o número de experimentos de Bernoulli, o número de ocorrências do evento de interesse, e o nível de confiança, o usuário pode variar os valores do limite superior e limite inferior da probabilidade de ocorrência do evento. O valor de alfa/2 é igual à soma das probabilidades dos segmentos em vermelho. Quando o valor de alfa/2 para o correspondente limite for igual a (100 – nível de confiança)/2 %, os segmentos para valores acima ou abaixo do número de ocorrência do evento ficarão verdes e os valores dos correspondentes limites do intervalo de confiança serão as probabilidades selecionadas na tela à esquerda (figura 15.10). Experimente!

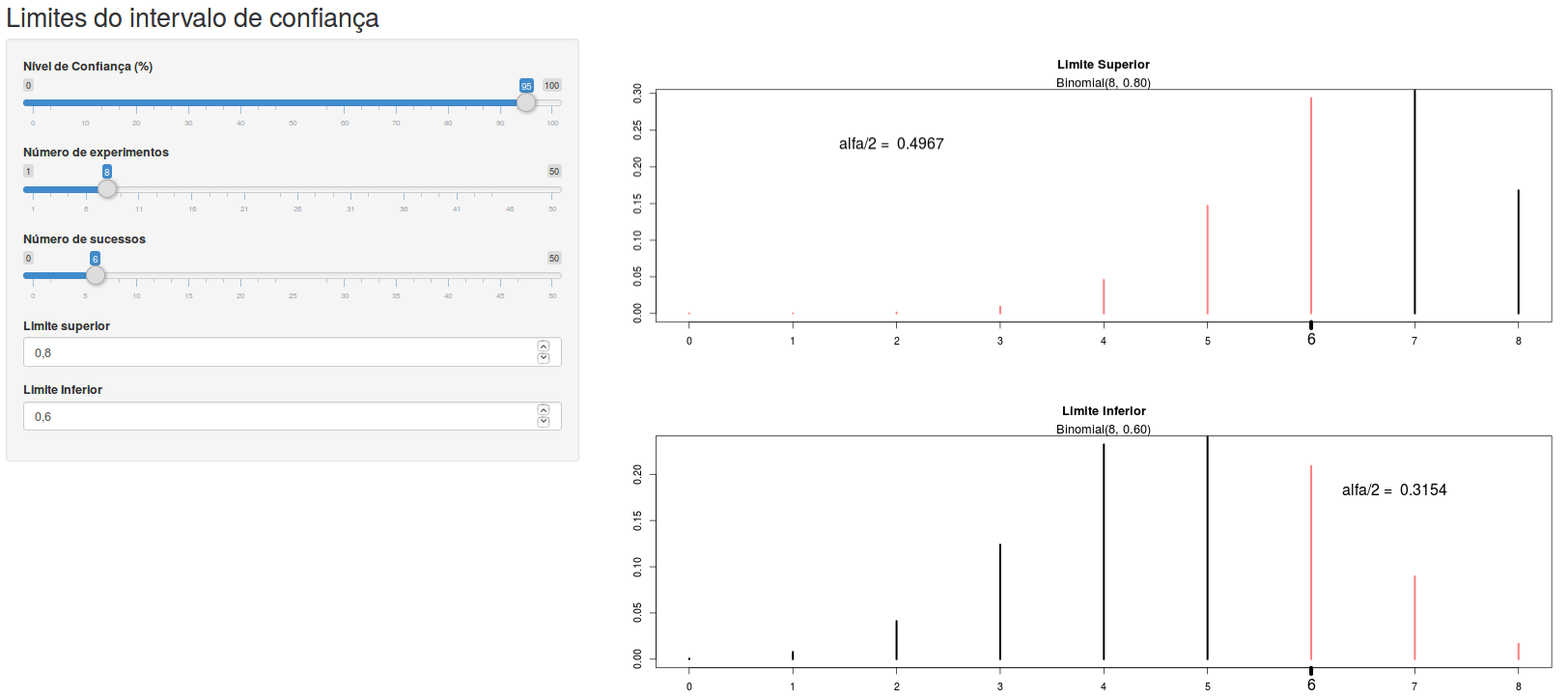
Figura 15.9: Aplicação que permite encontrar os limites do intervalo de confiança para a probabilidade de uma distribuição binomial, manipulando os valores do limite superior e inferior à esquerda da tela, uma vez selecionados os valores do nível de confiança, número de experimentos de Bernoulli e número de sucessos.

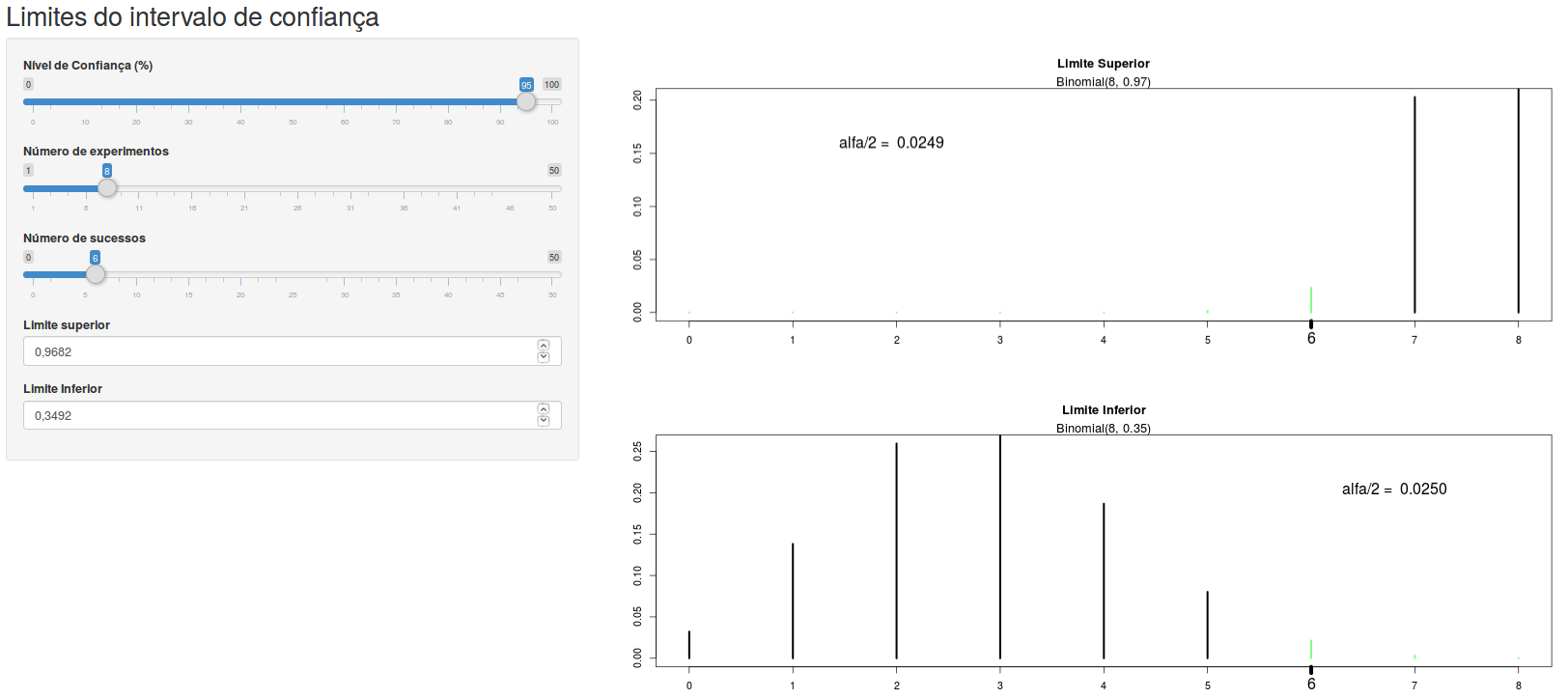
Figura 15.10: Usando a aplicação da figura 15.9, com o nível de confiança igual 95%, número de experimentos = 8 e número de sucessos = 6. Os limites do intevalo de confiança são mostrados no painel à esquerda.

Para o exemplo considerado, o intervalo de confiança exato é dado por:

\(0,3492 \leq p \leq 0,9682\)

O limite inferior é ligeiramente inferior ao obtido utilizando a aproximação da normal com a correção de continuidade, mas o limite superior é bastante inferior ao calculado pela aproximação, e obviamente menor que 1.

15.7 Tipos de testes (bilateral ou unilateral)

O conteúdo desta seção pode ser visualizado neste vídeo.

Existem duas formas de realizarmos um teste estatístico. Se nosso interesse for em avaliar se há uma diferença em relação ao valor definido para a H₀, tanto positiva como negativa, temos o teste bilateral (two-sided test). No exemplo das seções anteriores, esse foi o tipo de teste que realizamos, porque, para rejeitá-la, é preciso um desvio suficiente grande em relação à hipótese nula em qualquer sentido.

Às vezes, porém, pode-se supor que uma diferença real possa ocorrer somente em um sentido, de tal forma que, se ocorrer uma diferença no outro sentido, isso é devido ao acaso. Nesse caso, a hipótese alternativa se restringe a um efeito em um único sentido. Por exemplo, vamos supor que um medicamento esteja sendo comparado com o placebo para o tratamento de alguma condição de saúde, e um desfecho que está sendo avaliado é algum efeito adverso que esse medicamento possa causar. Os investigadores acreditam que, se houver diferença na proporção de efeitos adversos devido ao medicamento em relação ao placebo, o medicamento deverá ter uma maior proporção de efeitos adversos do que o placebo, e qualquer diferença observada no sentido contrário é devida ao acaso. Sendo \(RR\) o risco relativo para o efeito adverso do medicamento em relação ao placebo, a hipótese nula será \(RR \le 1\), e a hipótese alternativa será \(RR > 1\), ou seja, a hipótese nula será rejeitada somente se o RR foi maior do que valor crítico, determinado a partir do nível de significância (\(\alpha\)) e da distribuição da estatística utilizada. Nesse caso, o teste é chamado de teste unilateral (one-sided test).

A figura 15.11 compara a região crítica de um teste bilateral com a região crítica de um teste unilateral com o mesmo nível de significância, supondo que a região crítica do teste unilateral corresponda a desvios positivos. Nesse teste unilateral, o nível de significância corresponde a uma única cauda da distribuição (área vermelha + área rosa na cauda superior), enquanto que, em um teste bilateral, o valor de \(\alpha\) é dividido entre as duas caudas da distribuição. Podemos verificar que, para valores entre \(t_{1-\alpha}\) e \(t_{1-\alpha/2}\), a hipótese nula seria rejeitada no teste unilateral, mas não seria rejeitada em um teste bilateral. Daí a importância de se especificar o tipo de teste de antemão, para que o resultado do estudo não influencie a escolha do tipo de teste.

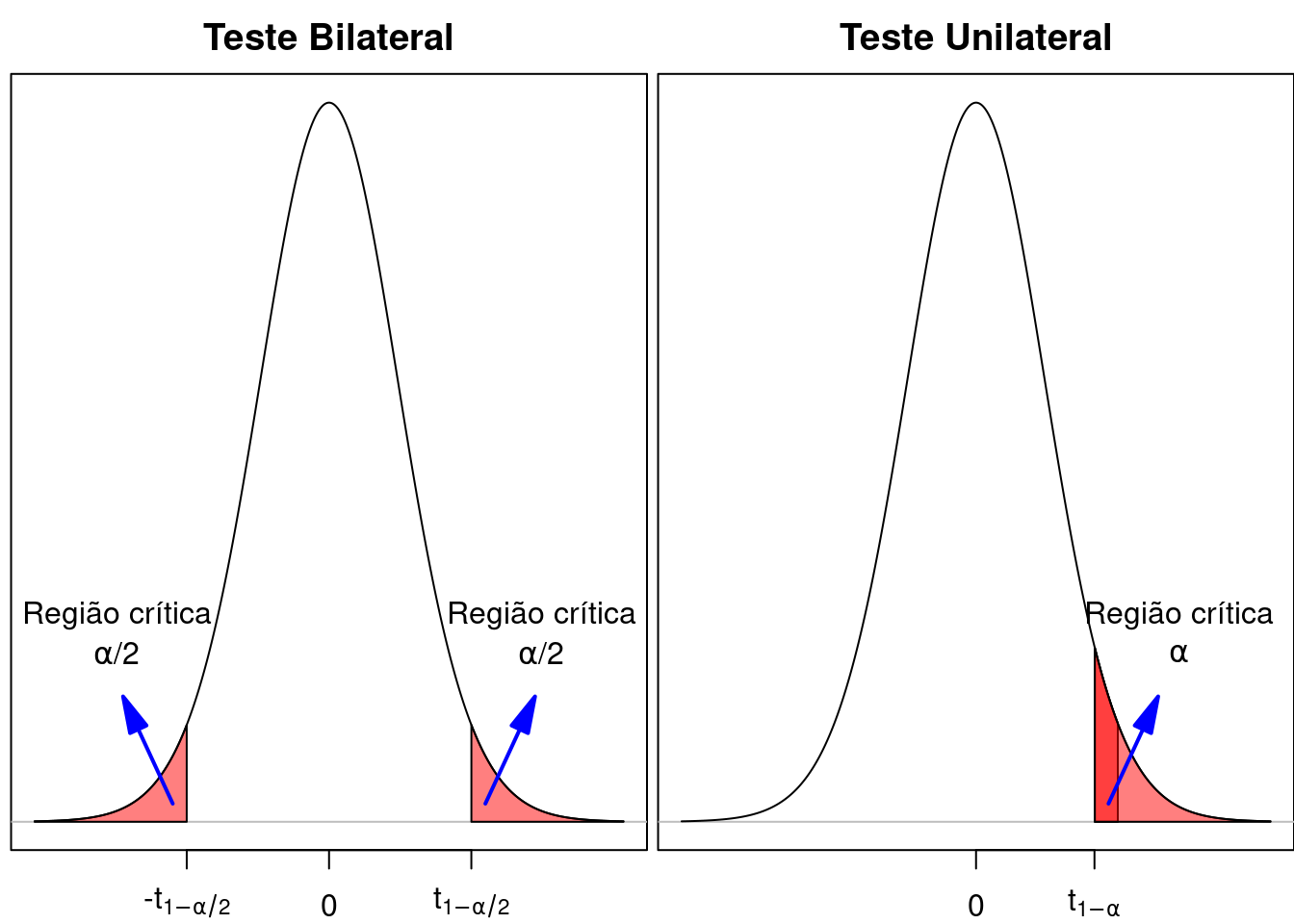
Figura 15.11: Comparação das regiões críticas de um teste unilateral (à direita) e bilateral (à esquerda). Para um teste unilateral superior, a região crítica é a união das áreas de cor vermelha e rosa na cauda superior do gráfico.

15.7.1 Exemplos de testes unilaterais

Vamos fazer uma pequena alteração no cenário que utilizamos na seção 15.3. Vamos supor que a distribuição dos valores da glicemia de jejum em uma população de pessoas não diabéticas seja gaussiana ou normal, mas que queiramos testar a hipótese de que a média de glicemia de jejum nessa população não seja maior do que 85 mg/dl, a partir de uma amostra de tamanho 36, extraída dessa população. Um teste de hipótese formalizado dessa forma é chamado de teste unilateral, porque nós iremos rejeitar a hipótese nula se o valor da média de glicose obtida na amostra for suficientemente maior do que a média estabelecida pela hipótese nula. A diferença desse cenário para o anterior é que, em um teste bilateral, a hipótese nula era de que o parâmetro avaliado, nesse caso a média da glicose, era igual a um dado valor (85 mg/dl).

Os passos para a realização de um teste de hipótese unilateral são os mesmos de um teste bilateral. Nesse exemplo, no primeiro passo, nós expressamos a hipótese nula, dizendo que a variável glicemia de jejum, denominada por X, segue uma distribuição normal, onde a média é menor ou igual a 85 mg/dl:

H₀: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu \le 85\ mg/dl\)

H₁: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu > 85\ mg/dl\)

No segundo passo, vamos utilizar a mesma estatística utilizada no teste bilateral. Vamos selecionar uma amostra aleatória da população com um certo número de elementos (n), vamos calcular a média da amostra e vamos obter a estatística T a partir da amostra:

\[\begin{align} T =\frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}} \end{align}\]

Vamos, em seguida, escolher o nível de significância igual a 5%. Com isso, e considerando que a estatística T, definida acima, segue a distribuição t de Student com n-1 graus de liberdade, a figura 15.12 mostra o gráfico da distribuição de t, supondo que a hipótese nula seja verdadeira, e um ponto correspondente ao quantil \(t_{n-1,1-\alpha}\) da distribuição t que delimita uma região (em vermelho) cuja área é igual a \(\alpha\) (a probabilidade de se obter um valor de t acima \(t_{n-1, 1-\alpha}\)). Essa é a região crítica desse teste unilateral, correspondente à região de rejeição da hipótese nula.

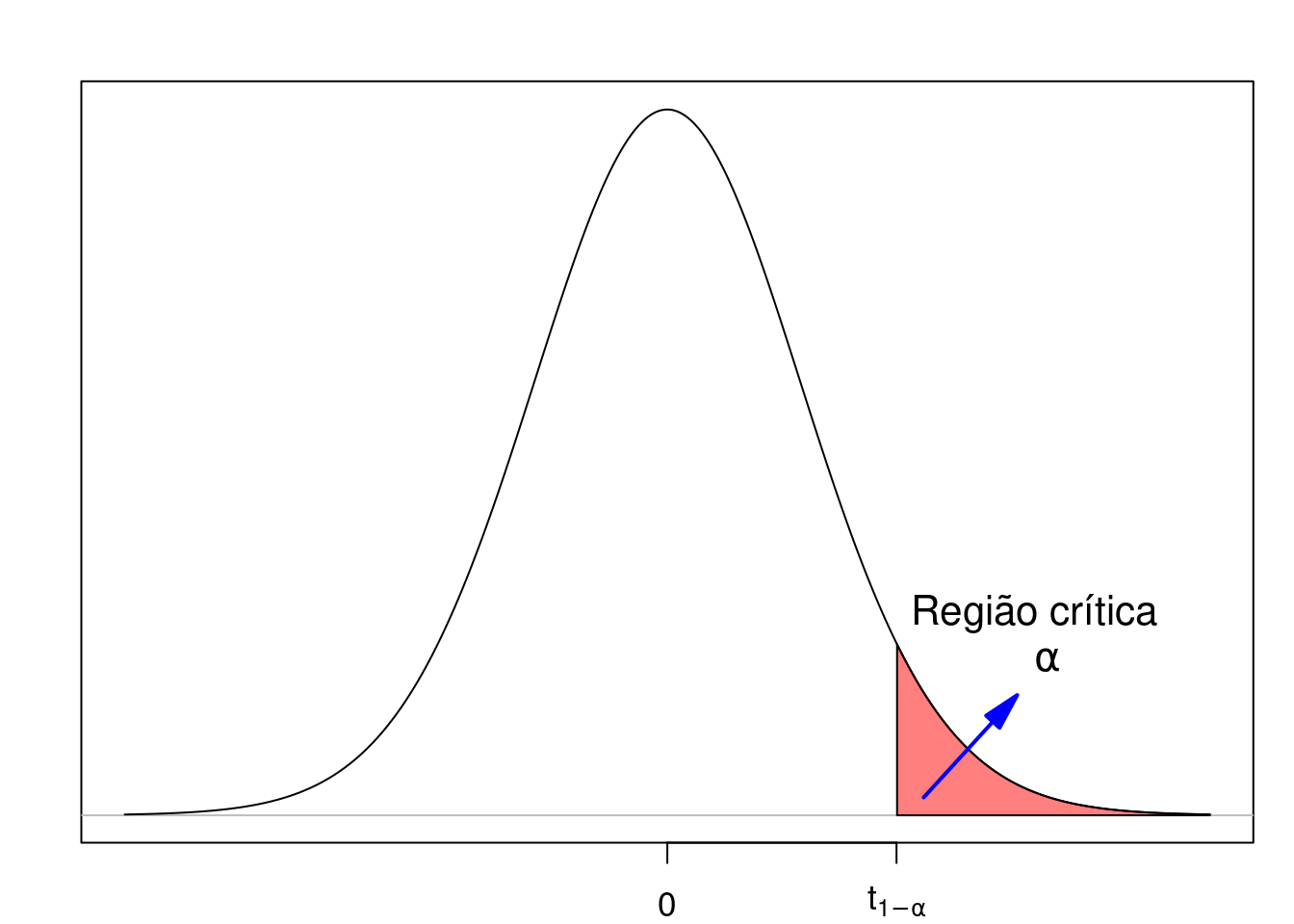
Figura 15.12: Região crítica na cauda superior em um teste unilateral.

Para esse exemplo, o valor crítico \(t_{n-1,1-\alpha} = t_{35; 0,95}\) é calculado no R da seguinte forma (n = 36):

qt(.95, 35)

## [1] 1.689572

Então \(t_{35; 0,95}\) = 1,69.

Ao definirmos a estatística a ser utilizada, o valor de \(\alpha\) e, consequente, a região crítica do teste, procedemos à seleção da amostra do estudo, a partir da qual o valor da estatística será calculado e comparado com o valor crítico.

Vamos supor que a amostra da população gerou os seguintes resultados:
\(\bar{x}\) = 92 mg/dl
n = 36
s = 16 mg/dl

Substituindo os valores na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{92-85}{\frac{16}{\sqrt{36}}}=2,62 \end{aligned}\)

Como esse valor de t cai na região crítica (figura 15.13), nós rejeitamos a hipótese nula e dizemos que o resultado é estatisticamente significativo.

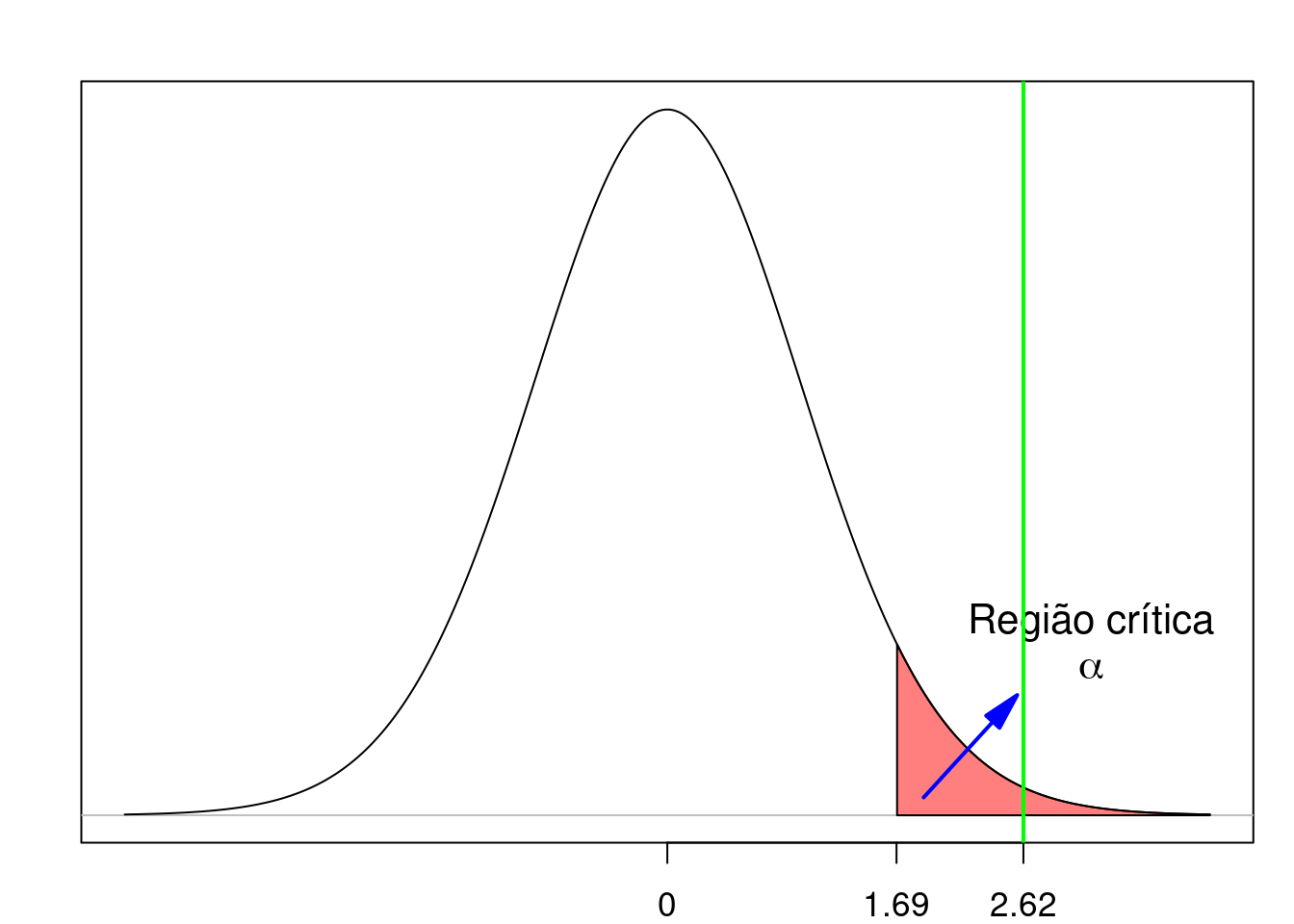
Figura 15.13: Exemplo de teste unilateral onde ocorre a rejeição da hipótese nula. A linha verde indica o valor da estatística t calculada a partir da amostra.

Vamos supor uma outra situação onde a amostra coletada gerou os seguintes resultados:
\(\bar{x} = 89\) mg/dl,
n = 36,
s = 16 mg/dl,

Substituindo os valores na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{89-85}{\frac{16}{\sqrt{36}}}=1,50. \end{aligned}\)

Como esse valor de t é menor que o valor crítico (figura 15.14), nós não rejeitamos a hipótese nula e dizemos que o resultado não é estatisticamente significativo.

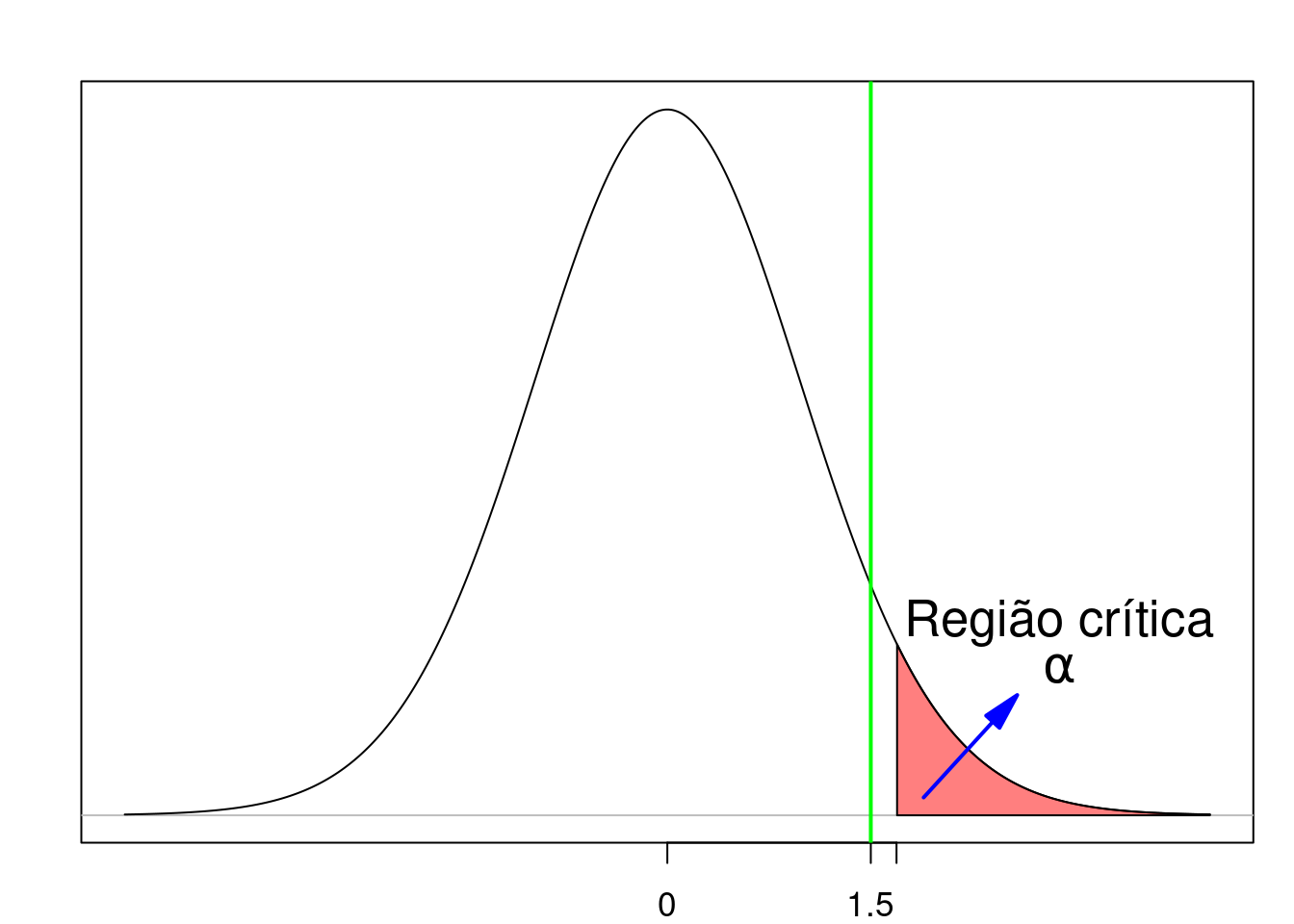
Figura 15.14: Exemplo de teste unilateral onde não ocorre a rejeição da hipótese nula. A linha verde indica o valor da estatística t calculada a partir da amostra.

Em geral, a menos que haja uma razão plausível para se utilizar um teste unilateral, recomenda-se a utilização de testes bilaterais. Mesmo quando há uma grande expectativa de que uma diferença de efeitos ocorra somente em um sentido, nós não podemos estar certos disso, e devemos considerar todas as possibilidades.

15.8 Valor de p (p-value)

O conteúdo desta seção e da seção 15.13 podem ser visualizados neste vídeo.

As probabilidades, sob a hipótese nula, de se obter um valor igual ou maior que o calculado para a estatística do teste ou de se obter um valor igual ou menor do que o calculado para a estatística do teste a partir da amostra são a base para obter o que se denomina valor de p (p value em inglês). Os programas estatísticos usualmente fornecem diretamente o valor de p quando realizamos testes de hipótese, naturalmente representado pela letra p.

Em um teste de hipótese para a média de uma variável aleatória X, que possui uma distribuição normal com média \(\mu\), mas não sabemos a variância dessa distribuição, calcula-se a estatística abaixo a partir de uma amostra aleatória de tamanho n da população:

\(\begin{aligned} T =\frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}} \end{aligned}\)

A figura 15.15 mostra a distribuição da estatística T, supondo que H₀ seja verdadeira. O valor da estatística t calculada a partir da amostra divide a região sob a distribuição da estatística T em duas partes.

A área em azul representa a probabilidade de se obter um valor da estatística de teste maior ou igual a t sob H₀ (p_superior). Para um teste unilateral, onde a região crítica é a cauda superior da distribuição da estatística de teste, o valor de p é igual a p_superior e representa, portanto, a probabilidade de se obter um valor da estatística de teste maior ou igual ao valor da estatística observado na amostra sob H₀.

A área em amarelo representa a probabilidade de se obter um valor da estatística de teste menor ou igual a t sob H₀ (p_inferior). Para um teste unilateral, onde a região crítica é a cauda inferior da distribuição da estatística de teste, o valor de p é igual a p_inferior e representa, portanto, a probabilidade de se obter um valor da estatística de teste menor ou igual ao valor da estatística observado na amostra sob H₀.

Para testes bilaterais, um dos critérios para estabelecer o valor de p é considerá-lo como o dobro da menor das probabilidades p_inferior e p_superior. Assim, para testes bilaterais:

\(\text{valor de p} = 2 . min(p_{superior}, p_{inferior})\)

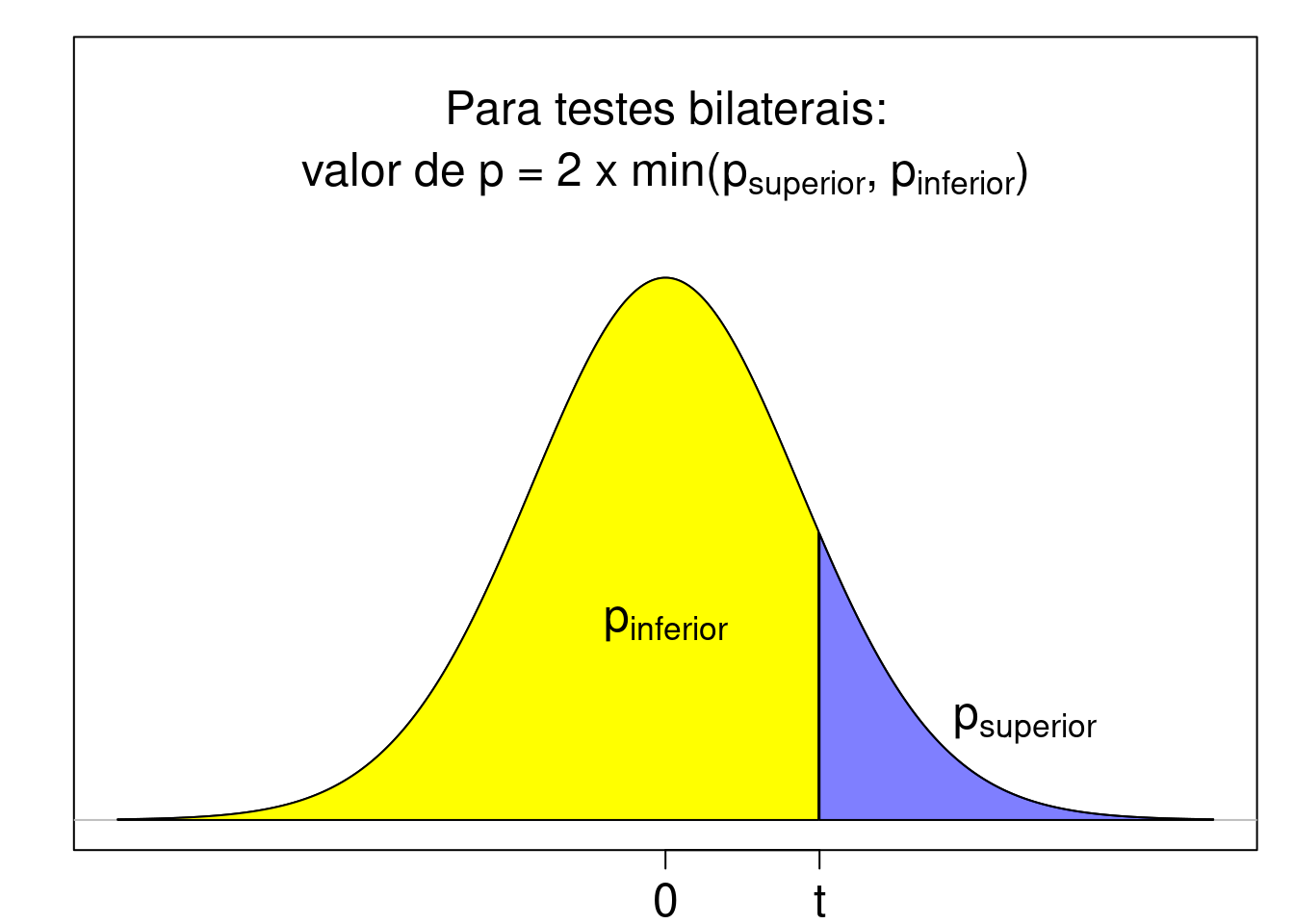
Figura 15.15: Definição do valor de p. A estatística calculada a partir da amostra, t, é mostrada no eixo X, juntamente com as áreas acima e abaixo dessa estatística.

Vamos calcular o valor de p para o teste de hipótese para a média da glicemia de jejum em uma população de não diabéticos, que possui uma distribuição normal com média \(\mu\), mas não sabemos a variância dessa distribuição, em quatro situações diferentes, já apresentadas nas seções anteriores.

As duas primeiras situações consideram um teste de hipótese unilateral, com nível de significância igual a 5%, com as seguintes hipóteses nulas e alternativas:

H₀: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu \le 85\ mg/dl\)

H₁: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu > 85\ mg/dl\)

Vamos supor que a amostra extraída aleatoriamente da população gerou os seguintes resultados:

\(\bar{x}\) = 92 mg/dl
n = 36
s = 16 mg/dl
\(t_{critico} = t_{35; 0,95} = 1,69\)

Substituindo os valores acima na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{92-85}{\frac{16}{\sqrt{36}}}=2,62 \end{aligned}\)

O valor de p é a área em azul na figura 15.16, área sob a distribuição além do valor de t calculado a partir da amostra (2,62), que é a probabilidade de a estatística T assumir um valor maior ou igual a 2,62. O valor de t é maior do que o t_critico. Logo a hipótese nula é rejeitada.

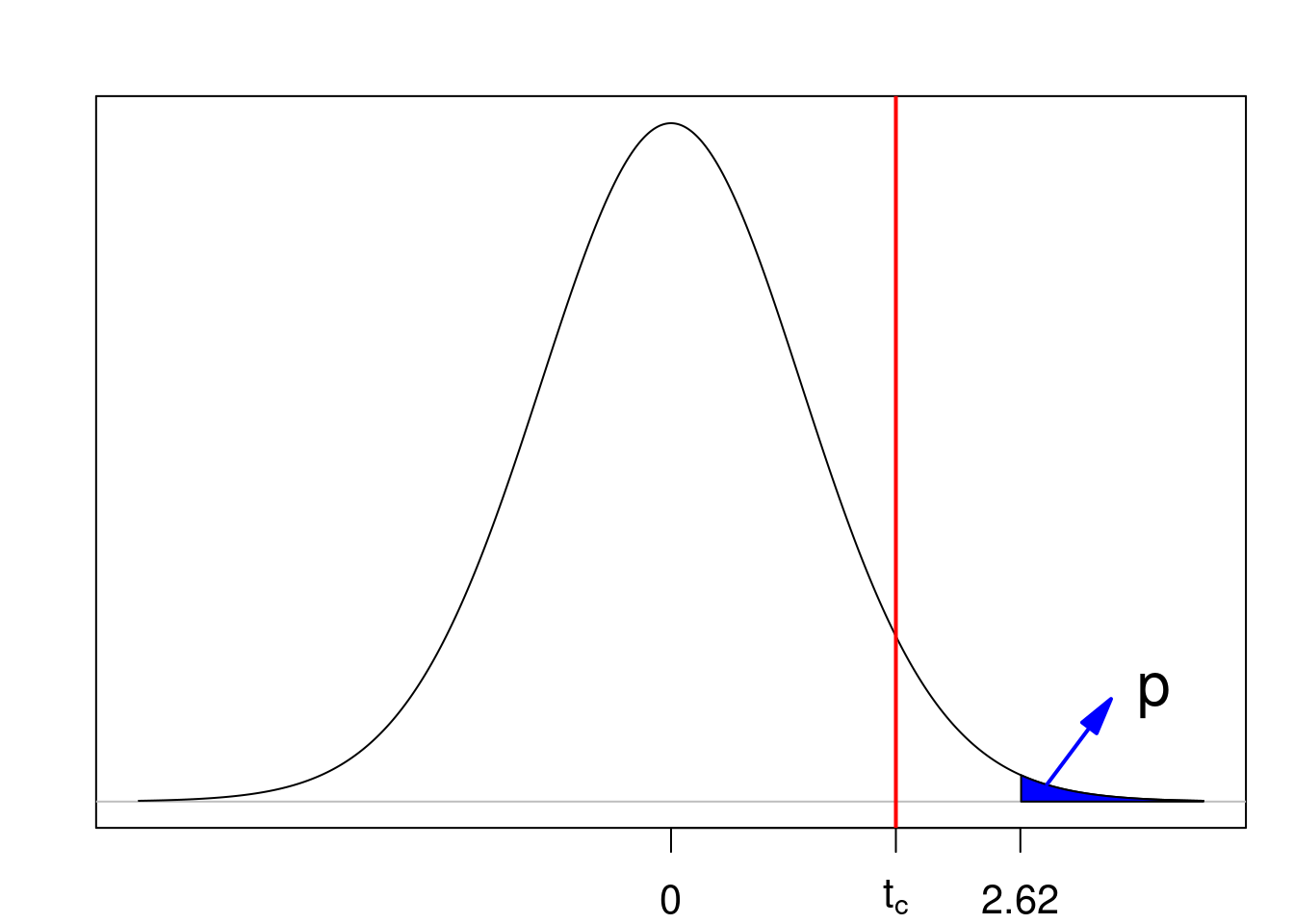
Figura 15.16: Valor de p para um teste unilateral onde a região crítica é a cauda superior da distribuição. A linha vermelha indica o valor crítico. Nesse exemplo, a hipótese nula é rejeitada.

O valor de p pode ser obtido no R por meio da expressão:

pt(2.62, df = 35, lower.tail = FALSE)

## [1] 0.006458247

Verificamos que o valor de p (0,006) é menor do que o nível de significância (5%) do teste.

Vamos agora manter o mesmo teste unilateral acima, mas vamos supor que a amostra extraída aleatoriamente da população gerou os seguintes resultados:

\(\bar{x}\) = 89 mg/dl
n = 36
s = 16 mg/dl
\(t_{critico} = t_{35; 0,95} = 1,69\)

Substituindo os valores acima na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{89-85}{\frac{16}{\sqrt{36}}}=1,5 \end{aligned}\)

O valor de p é a área em azul na figura 15.17, área sob a distribuição além do valor de t calculado a partir da amostra (1,5), que é a probabilidade de a estatística T assumir um valor maior ou igual a 1,5. O valor de t é menor do que o t_critico. Logo a hipótese nula não é rejeitada.

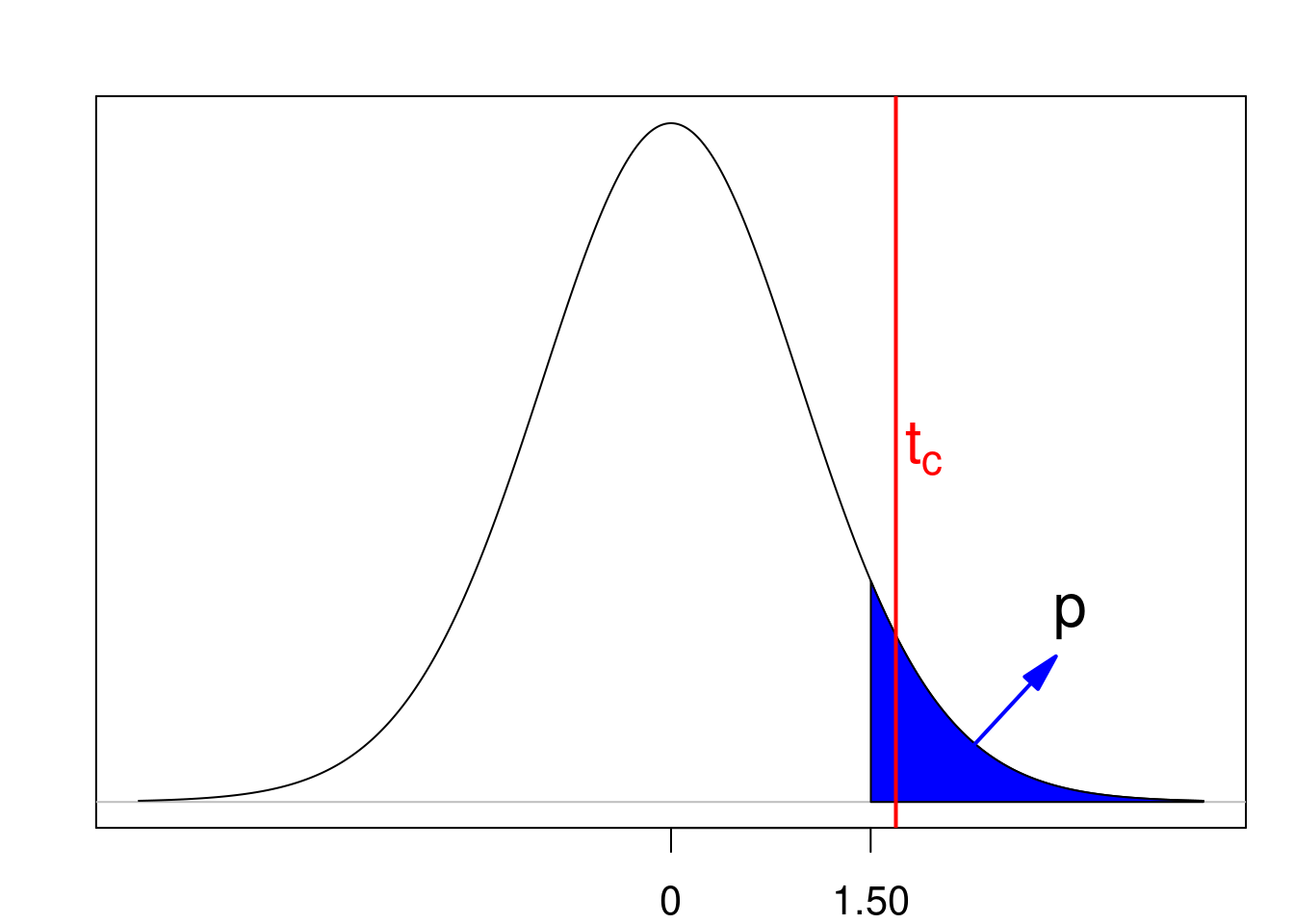
Figura 15.17: Valor de p para um teste unilateral onde a região crítica é a cauda superior da distribuição. A linha vermelha indica o valor crítico. Nesse exemplo a hipótese nula não é rejeitada.

O valor de p pode ser obtido no R por meio da expressão:

pt(1.5, df = 35, lower.tail = FALSE)

## [1] 0.07129092

Verificamos que o valor de p (0,07) é maior do que o nível de significância (5%) do teste.

Vamos considerar agora um teste de hipótese bilateral, com nível de significância igual a 5%, com as seguintes hipóteses nulas e alternativas:

H₀: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu = 85\ mg/dl\)

H₁: glicemia de jejum ~ distribuição normal \(N(\mu, \sigma^2)\), com \(\mu \ne 85\ mg/dl\)

Vamos supor que a amostra extraída aleatoriamente da população gerou os seguintes resultados:

\(\bar{x}\) = 92 mg/dl
n = 36
s = 16 mg/dl
\(t_{critico} = t_{35; 0,975} = 2,03\)

Substituindo os valores acima na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{92-85}{\frac{16}{\sqrt{36}}}=2,62 \end{aligned}\)

Esse valor de t é maior do que o t_critico. Logo a hipótese nula é rejeitada.

O valor de p_superior é a área em azul na figura 15.18, área sob a distribuição além do valor de t calculado a partir da amostra (2,62), que é a probabilidade de a estatística T assumir um valor maior ou igual a 2,62. O valor de p_inferior é a área em amarelo na figura 15.18, área sob a distribuição aquém do valor de t calculado a partir da amostra (2,62), que é a probabilidade de a estatística T assumir um valor menor ou igual a 2,62.

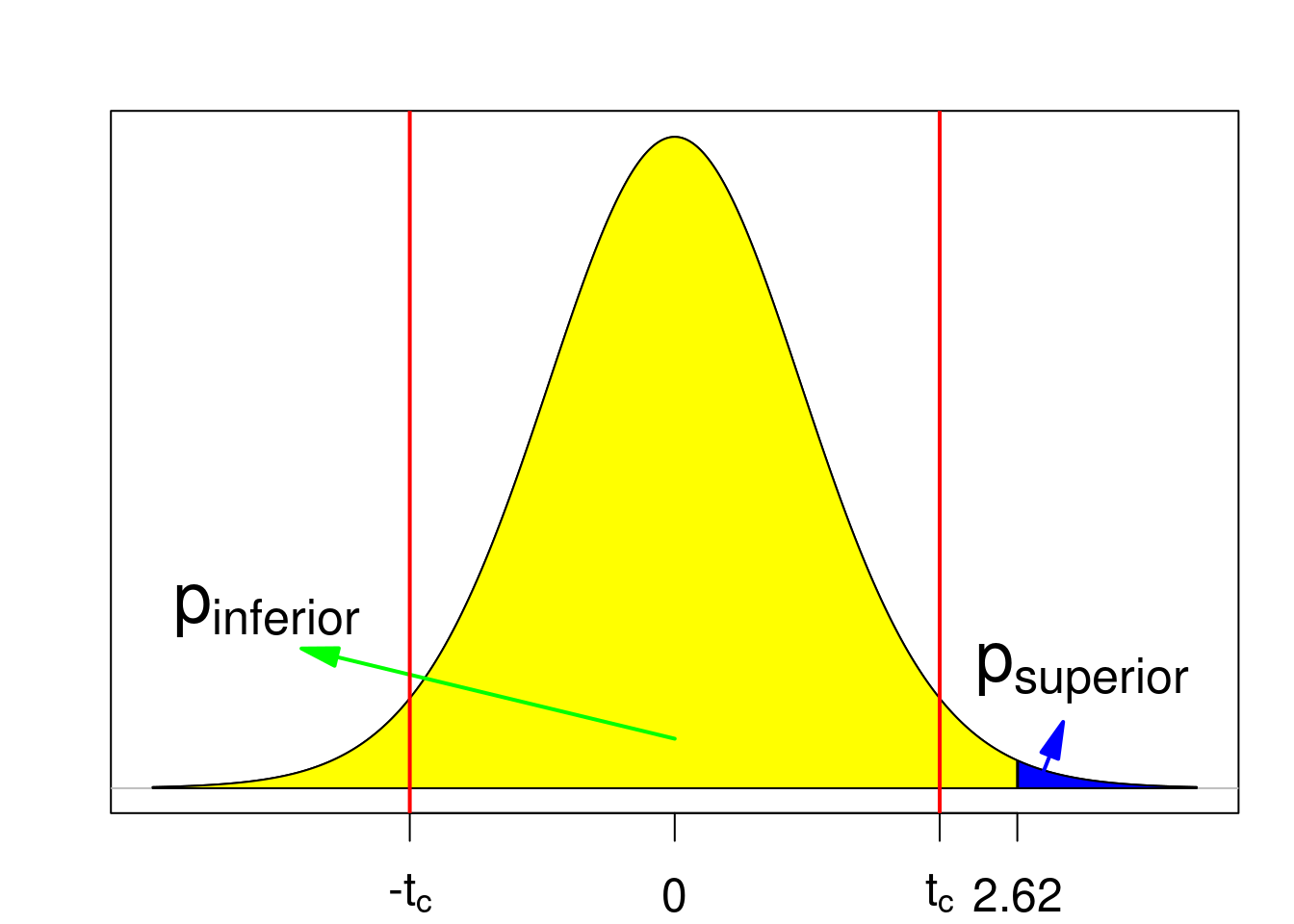
Figura 15.18: Valor de p para um teste bilateral. As linhas vermelhas indicam os valores críticos. Nesse exemplo, a hipótese nula é rejeitada.

O valor de p_superior pode ser obtido no R por meio da expressão a seguir, dando um valor igual a 0,0065:

pt(2.62, df = 35, lower.tail = FALSE)

## [1] 0.006458247

O valor de p_inferior pode ser obtido no R por meio da expressão a seguir, dando um valor igual a 0,9935 (complemento de p_superior):

pt(2.62, df = 35, lower.tail = TRUE)

## [1] 0.9935418

Como o valor de p_superior é menor do que o valor de p_inferior, o valor de p para esse teste é o dobro do valor de p_superior, sendo igual a 0,013. Verificamos que o valor de p (1,3%) é menor do que o nível de significância do teste (5%).

Finalmente vamos agora manter o mesmo teste bilateral acima, mas vamos supor que a amostra extraída aleatoriamente da população gerou os seguintes resultados:
\(\bar{x}\) = 89 mg/dl
n = 36
s = 16 mg/dl
\(t_{critico} = t_{35; 0,975} = 2,03\)

Substituindo os valores acima na expressão (15.3), obtemos:

\(\begin{aligned} t =\frac{92-85}{\frac{16}{\sqrt{36}}}=1,5 \end{aligned}\)

Esse valor de t está fora da região crítica. Logo a hipótese nula não é rejeitada.

O valor de p_superior é a área em azul na figura 15.19, área sob a distribuição além do valor de t calculado a partir da amostra (1,5), que é a probabilidade de a estatística t assumir um valor maior ou igual a 1,5. O valor de p_inferior é a área em amarelo na figura 15.19, área sob a distribuição aquém do valor de t calculado a partir da amostra, que é a probabilidade de a estatística t assumir um valor menor ou igual a 1,5.

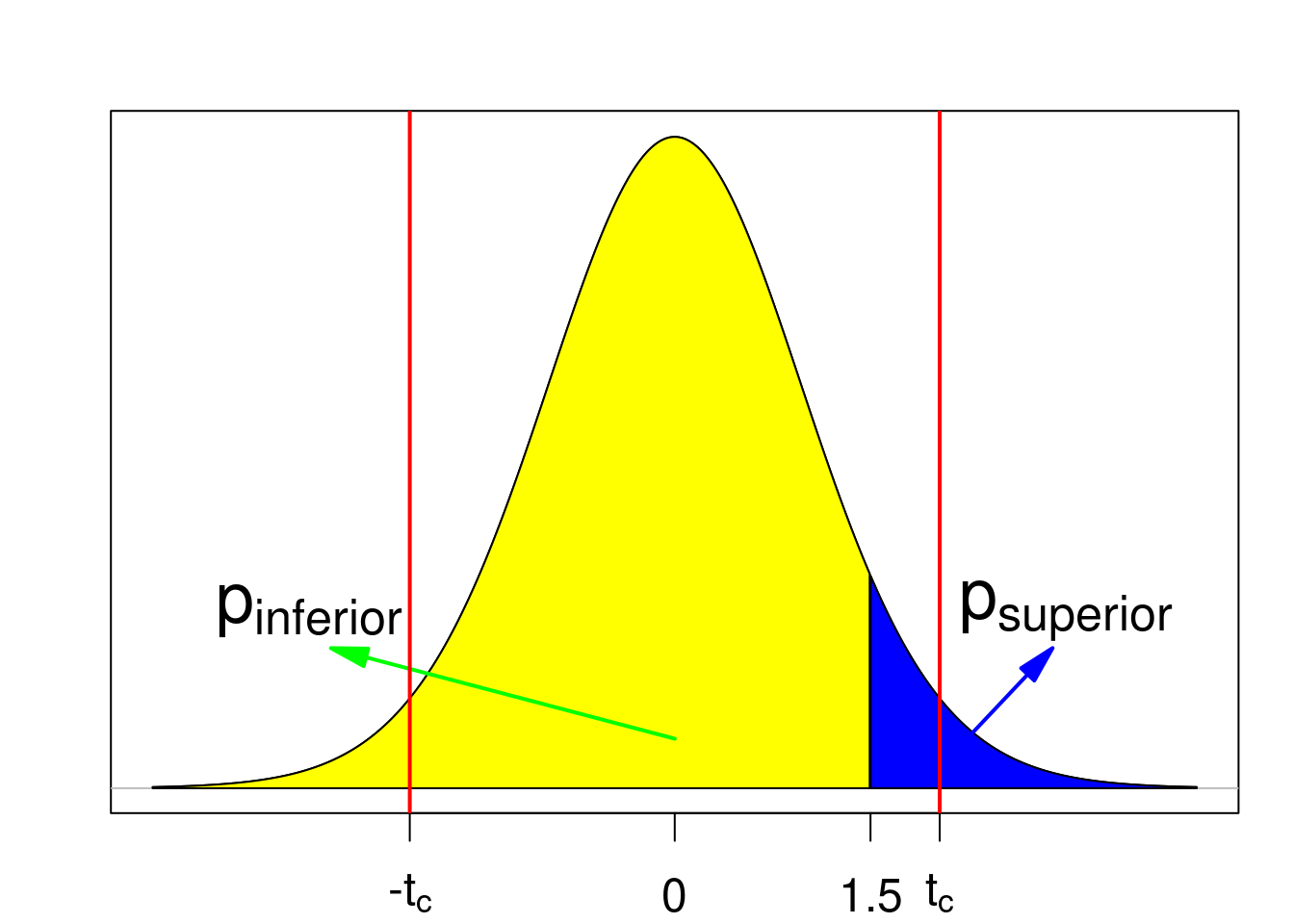
Figura 15.19: Valor de p para um teste bilateral. As linhas vermelhas indicam os valores críticos. Nesse exemplo, a hipótese nula não é rejeitada.

O valor de p_superior pode ser obtido no R por meio da expressão a seguir, dando um valor igual a 0,071:

pt(1.5, df = 35, lower.tail = FALSE)

## [1] 0.07129092

O valor de p_inferior pode ser obtido no R por meio da expressão a seguir, dando um valor igual a 0,929 (complemento de p_superior):

pt(1.5, df = 35, lower.tail = TRUE)

## [1] 0.9287091

O valor de p para esse teste é o dobro do valor de p_superior, sendo igual a 0,142. Verificamos que o valor de p (14,2%) é maior do que o nível de significância do teste (5%).

Ao calcularmos o valor de p para um teste de hipótese, se ele for menor do que \(\alpha\), a hipótese nula é rejeitada; se p for maior ou igual a \(\alpha\), a hipótese nula não é rejeitada. É sempre mais conveniente apresentar o valor de p em um teste estatístico do que simplesmente dizer se ele é maior ou menor do que \(\alpha\). Se o valor de p for pequeno, significa que os dados amostrais obtidos são muito improváveis de terem ocorrido se a hipótese nula fosse verdade, ou seja, essa hipótese ou é falsa ou temos uma amostra muito improvável.

Para testes bilaterais, há mais de uma proposta para calcular o valor de p. Uma alternativa à apresentada nesta seção é mostrada na seção 15.12.

15.9 Erro tipo I (erro \(\boldsymbol{\alpha}\)) e erro tipo II (erro \(\boldsymbol{\beta}\))

O conteúdo desta seção pode ser visualizado neste vídeo.

Em todo processo decisório onde temos de escolher entre dois cursos de ação, sempre podemos cometer erros. O mesmo acontece em um teste de hipótese, quando utilizamos o processo descrito nas seções anteriores. Basicamente dois tipos de erros podem ocorrer, não simultaneamente:

1) Erro tipo I (erro \(\boldsymbol{\alpha}\)): esse erro ocorre quando rejeitamos a hipótese nula quando de fato ela é verdadeira. A probabilidade de ocorrer esse erro é \(\alpha\). Isso pode acontecer quando extraímos uma amostra da população e a estatística calculada a partir dessa amostra cai na região crítica. Ao fixarmos \(\alpha\), fixamos a probabilidade desse erro.

No primeiro cenário da seção 15.3, a hipótese nula foi rejeitada. Nesse caso, podemos ter cometido o erro tipo I.

2) Erro tipo II (erro \(\boldsymbol{\beta}\)): esse erro ocorre quando não rejeitamos a hipótese nula quando de fato ela é falsa. A probabilidade de ocorrer esse erro é \(\beta\). Isso acontece quando extraímos uma amostra da população e a estatística calculada a partir dessa amostra não cai na região crítica.

No segundo cenário, apresentado na seção 15.3.1, a hipótese nula não foi rejeitada. O valor da estatística t caiu fora da região crítica (linha vertical verde na figura 15.20) e a hipótese nula não é rejeitada. Se a distribuição verdadeira da glicemia de jejum nessa população tivesse a média 90 mg/dl (e não 85 mg/dl), estaríamos cometendo o erro tipo II, porque não rejeitamos a hipótese nula. O gráfico para a estatística t para a hipótese H₁ (\(\mu\) = 90 mg/dl) seria a curva sob H₁ na figura 15.20. A probabilidade do erro tipo II para a hipótese H₁ é dada pela área do gráfico sob H₁ situada fora da região crítica do teste (área amarela na figura 15.20).

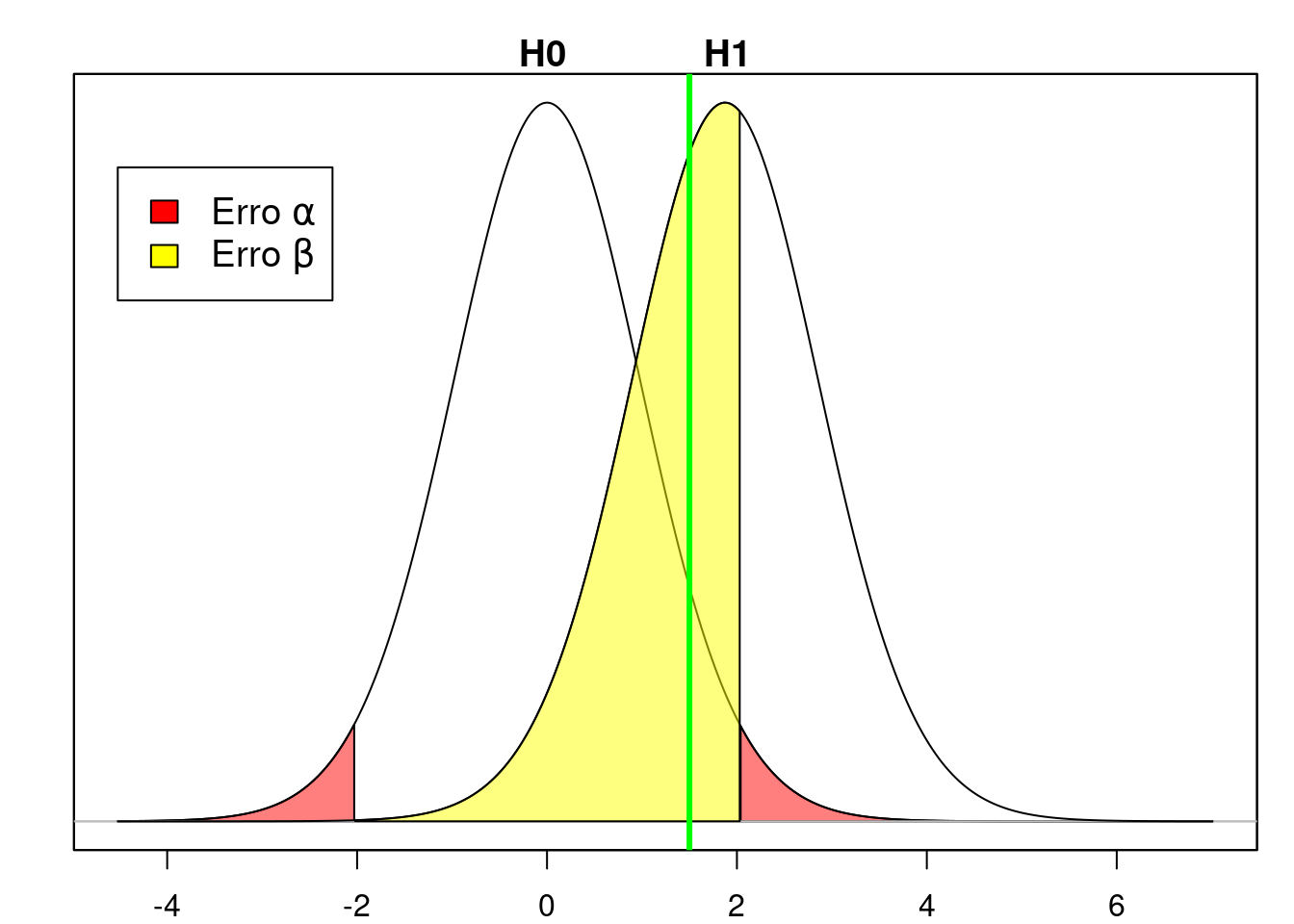
Figura 15.20: O valor da estatística no teste de hipótese é 1,50 (reta vertical verde) e está localizada fora da região crítica do teste. Portanto a hipótese nula não é rejeitada. Se a hipótese H₁ fosse a verdadeira, então estaríamos cometendo o erro \(\beta\), cuja probabilidade seria a área amarela sob o gráfico definido por H₁.

Usando o R, a probabilidade do erro tipo II (se a média 90 mg/dl for a verdadeira) é dada pela expressão a seguir e o valor é de 55,4%.

pt(2.03, 35, ncp = 1.875, lower.tail=TRUE) - 
    pt(-2.03, 35, ncp = 1.875, lower.tail=TRUE)

## [1] 0.5541548

O valor da função pt(2.03, 35, ncp = 1.875, lower.tail=TRUE) fornece a probabilidade de obtermos um valor de t abaixo de 2,03 (limite superior da região crítica) para a distribuição t de Student definida por H₁ (por isso o parâmetro ncp = 1.875). Vamos chamar esse valor de p1. Se utilizássemos ncp = 0, estaríamos calculando a probabilidade de t abaixo de 2,06 para a distribuição t de Student definida por H₀.

O valor de ncp define o deslocamento da distribuição t de Student em relação à distribuição sob a hipótese nula. esse deslocamento é calculado, substituindo-se na estatística t dada pela expressão (15.3) o valor de \(\bar{x}\) pela média da distribuição H₁ (90 mg/dl) para a qual desejamos calcular a probabilidade do erro tipo II e o valor de \(\mu\) pela média da distribuição sob a hipótese nula. Logo:

\(\begin{aligned} ncp =\frac{90-85}{\frac{16}{\sqrt{36}}}= 1,875 \end{aligned}\)

O valor da função pt(-2.03, 35, ncp = 1.875, lower.tail=TRUE) fornece a probabilidade de obtermos um valor de t abaixo de -2,03 (limite inferior da região crítica) para a distribuição t de Student definida por H₁. Esse valor (muito pequeno) tem que ser subtraído do valor p1, para dar a área da distribuição de H₁ fora da região crítica do teste.

Assim sempre podemos estar cometendo um dos dois erros em um teste de hipótese. Se rejeitarmos a hipótese nula, podemos estar cometendo o erro tipo I. Se não a rejeitarmos, podemos cometer o erro tipo II.

Enquanto a probabilidade do erro tipo I (\(\alpha\)) é definida a priori pelos investigadores, há infinitos valores para a probabilidade do erro tipo II, dependendo de qual hipótese é a verdadeira (no exemplo acima, ela depende de qual é a verdadeira média da glicemia de jejum na população). Para cada valor diferente para a média real, teríamos um valor diferente para a probabilidade do erro tipo II (\(\beta\)).

A figura 15.21 mostra a variação da probabilidade do erro \(\beta\) em função da hipótese alternativa. A probabilidade do erro \(\beta\) aumenta quando a média sob a hipótese alternativa se aproxima da média sob a hipótese nula (sendo igual a 1 – \(\alpha\) quando a diferença entre elas é infinitesimal, ponto em azul no gráfico). À medida que a média sob a hipótese alternativa se afastar da média sob a hipótese nula, a probabilidade do erro tipo II irá diminuir.

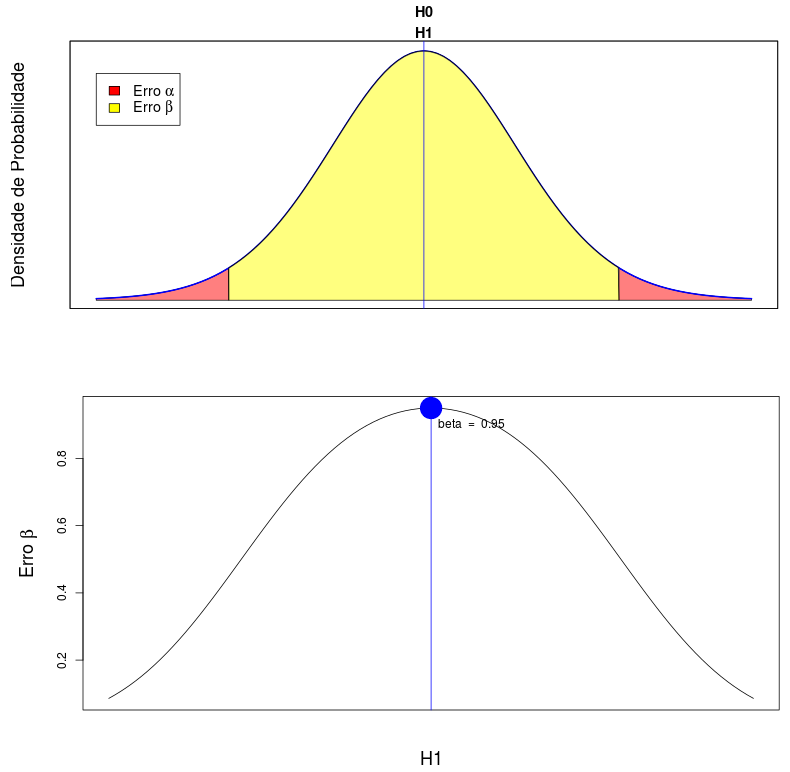
Figura 15.21: O gráfico na parte inferior mostra a relação entre a probabilidade do erro \(\beta\) em função de diferentes hipóteses alternativas (\(\alpha\) foi fixado em 5% neste gráfico). O gráfico na parte superior indica a situação quando a hipótese alternativa difere infinitesimalmente da hipótese nula. Nessa situação, a probabilidade do erro \(\beta\) corresponde ao ponto azul no gráfico na parte inferior.

A aplicação Erros tipo I e tipo II (figura 15.22) permite ao leitor experimentar com diferentes hipóteses alternativas e valores de \(\alpha\) e verificar a variação da probabilidade do erro tipo II, tomando como hipótese nula uma distribuição normal, com média 85, desvio padrão igual a 16 e tamanho amostral igual a 36 (erro padrão da média amostral é igual a 2,67).

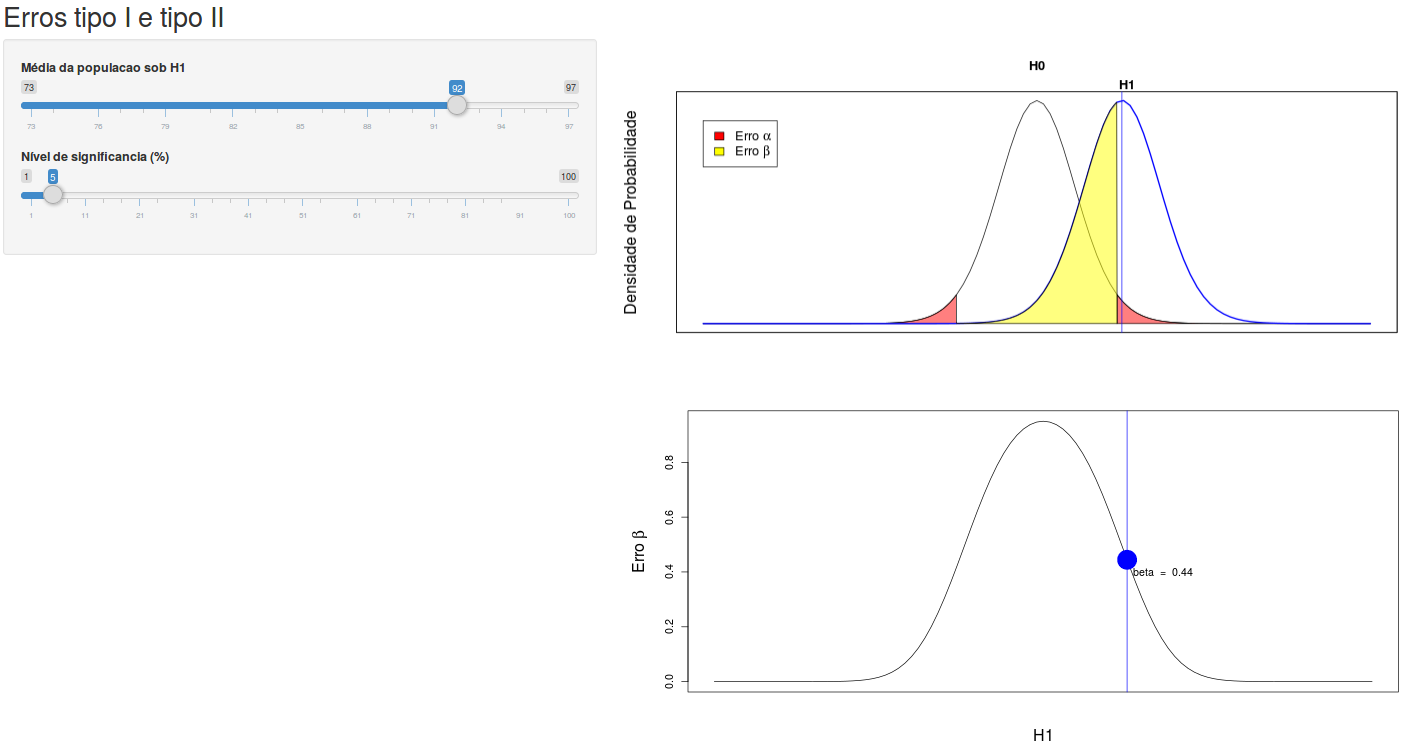
Figura 15.22: Aplicação que mostra a variação da probabilidade do erro tipo II (gráfico da parte inferior), tomando como hipótese nula uma distribuição normal com média 85 e desvio padrão igual a 16, e tamanho amostral igual a 36. O usuário pode selecionar o valor do erro tipo I e diferentes hipóteses alternativas (H₁, gráfico superior) e verificar a variação da probabilidade do erro tipo II.

A tabela 15.1 resume as quatro situações possíveis que podem ocorrer ao realizar um teste de hipótese.

Tabela 15.1: Situações possíveis em um teste de hipótese.

		Realidade
		H0 é Verdadeira	H0 é Falsa
Teste	Não Rejeitar H0	Decisão Correta	Erro Tipo II (\(\beta\))
Teste	Rejeitar H0	Erro Tipo I (\(\alpha\))	Decisão Correta

15.10 Exemplo de um teste hipótese no R Commander

Vamos fazer um teste t, utilizando o R Commander. Para isso vamos abrir o conjunto de dados juul2 do pacote ISwR (GPL-2 | GPL-3), conforme mostrado no capítulo 3. Vamos testar se a média da variável aleatória igf1 (insulin-like growth factor) é 360 \(\mu g/l\) na população estudada, considerando o nível de significância igual a 10%. Para isso, selecionamos a opção:

\[\text{Estatísticas} \Rightarrow \text{Médias} \Rightarrow \text{Teste t para uma amostra}\]

Na caixa de diálogo para realização do teste, selecionamos a variável igf1, o valor da média para a hipótese nula, o nível de confiança e clicamos em Ok (Figura 15.23).

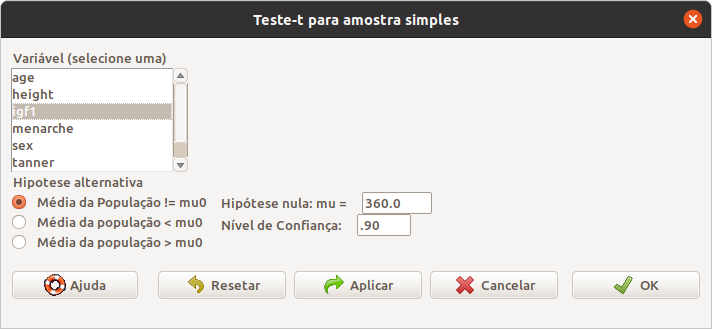
Figura 15.23: Parâmetros para a realização do teste t para uma amostra: variável, média sob a hipótese nula, nível de confiança \((1 - \alpha)\), e tipo de teste (nesse exemplo, a hipótese alternativa é que a média é diferente de 360 \(\mu g/l\)).

O resultado do teste é mostrado na figura 15.24 abaixo:

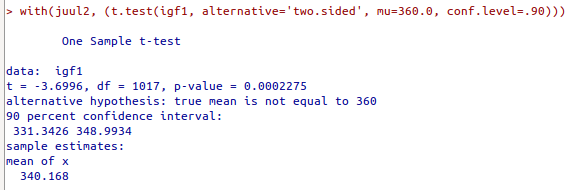
Figura 15.24: Resultado do teste t especificado na figura 15.23.

O resultado mostra o valor da estatística t calculada para a amostra, o número de graus de liberdade (df), o valor de p, a média da amostra e o intervalo de confiança com nível de confiança de 90%. O resultado é estatisticamente significativo e a hipótese nula é rejeitada.

15.11 Poder de um teste e tamanho amostral

O conteúdo desta seção pode ser visualizado neste vídeo.

Nos exemplos apresentados até agora, utilizamos amostras de tamanhos arbitrários. Nesta seção, vamos mostrar por que a escolha do tamanho da amostra, ou amostras, de um estudo é tão importante. Ao realizar uma análise estatística, seja ela um teste de hipótese, seja o cálculo do intervalo de confiança de um parâmetro populacional, estamos interessados em obter erros tipo I ou tipo II os menores possíveis, bem como intervalos de confiança com boa precisão.

Em um teste de hipótese, o erro tipo II (\(\beta\)) representa a probabilidade de não rejeitarmos a hipótese nula quando ela é falsa. O complemento de \(\beta\) (1 – \(\beta\)) significa então a probabilidade de rejeitarmos a hipótese nula quando ela é falsa. 1 – \(\beta\) é chamado de poder estatístico do teste.

Na seção 15.9, vimos que o erro \(\beta\), e consequentemente o poder estatístico, depende do valor do parâmetro sob a hipótese alternativa. A aplicação Poder Estatístico e Tamanho Amostral, cuja tela inicial é apresentada na figura 15.25, mostra o poder estatístico em função do desvio padrão, do tamanho amostral, do erro alfa e da distância entre a hipótese nula e uma hipótese alternativa possível. A hipótese nula corresponde a uma variável X ~ N(100, \(\sigma^2\)), ou seja, uma distribuição normal com média 100 e desvio padrão \(\sigma\), escolhido pelo usuário. A hipótese H₁ possui o mesmo desvio padrão da hipótese nula e média definida pelo usuário. O gráfico inferior mostra o poder estatístico para diferentes valores da média sob H₁ e o ponto em azul mostra o valor do poder do teste para a média sob a hipótese H₁ selecionada pelo usuário no painel à esquerda.

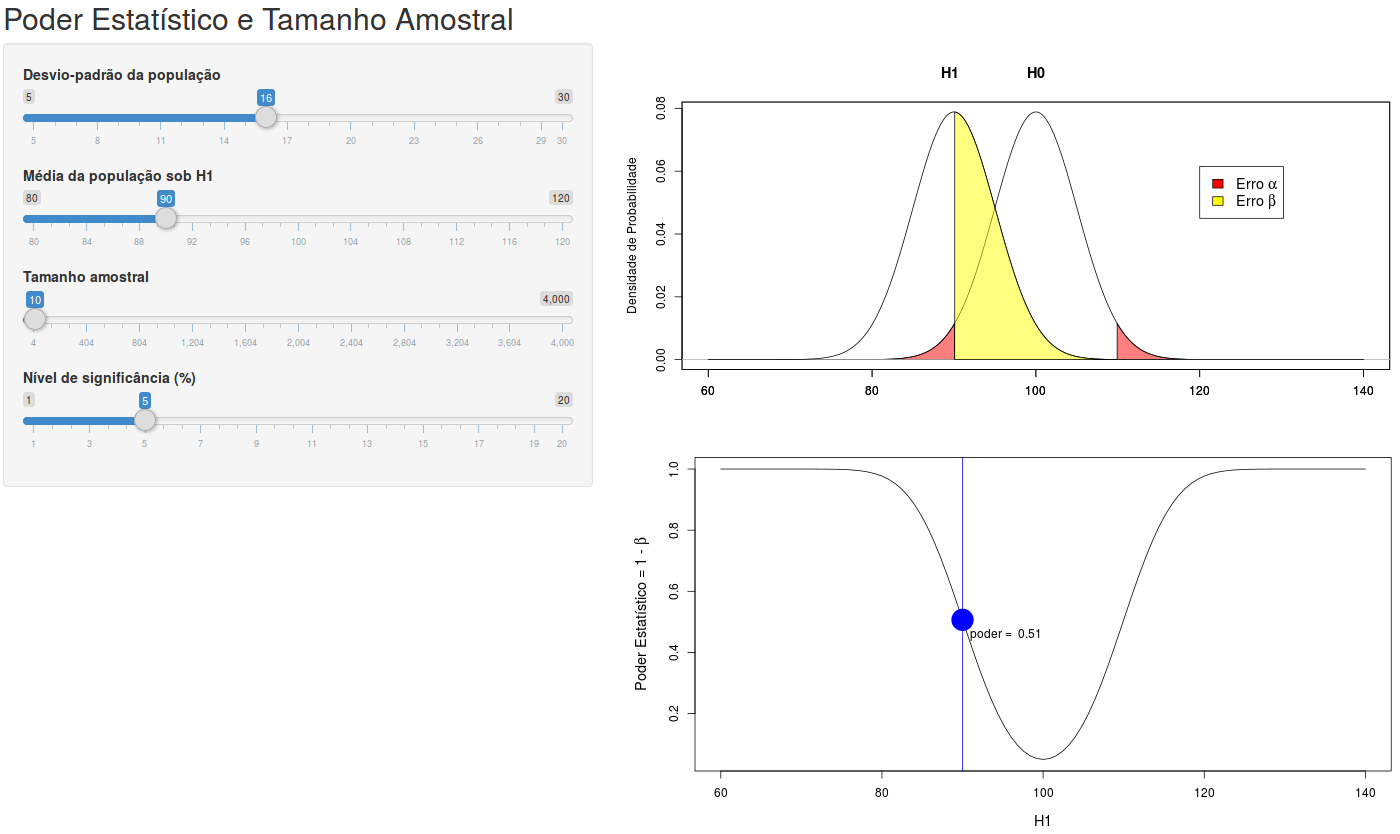
Figura 15.25: Aplicação que mostra o poder estatístico em função do desvio padrão, do tamanho amostral, do erro alfa e da distância entre a hipótese nula e uma hipótese alternativa possível. A hipótese nula corresponde a uma variável X ~ N(100, \(\sigma^2\)), ou seja, uma distribuição normal com média 100 e desvio padrão \(\sigma\), escolhido pelo usuário.

A figura 15.26 ilustra o efeito do desvio padrão sobre o poder estatístico. Ao reduzirmos o desvio padrão à metade, o poder estatístico subiu de 51% para 98%.

A figura 15.27 ilustra o efeito da diferença entre as médias sob a hipótese alternativa e nula, respectivamente, sobre o poder estatístico. Ao dobrarmos o valor da diferença, o poder estatístico também subiu de 51% para 98%.

A figura 15.28 ilustra o efeito do tamanho da amostra sobre o poder estatístico. Ao dobrarmos o tamanho da amostra, o poder estatístico subiu de 51% para 80%.

A figura 15.29 mostra o poder estatístico para diferentes valores da média sob a hipótese H₁ e para diferentes tamanhos amostrais. São mostradas três curvas para valores do tamanho amostral iguais a 4, 8 e 16, respectivamente. Observem que, para cada valor da média sob H₁, o poder estatístico aumenta com o tamanho amostral. Em um estudo experimental, não é possível controlar o desvio padrão da população, mas os investigadores podem ajustar o tamanho amostral, de modo que, se uma dada hipótese alternativa H₁ for verdadeira, então o estudo pode ter um poder estatístico preestabelecido para rejeitar a hipótese nula.

Um exemplo de cálculo de tamanho amostral é apresentado a seguir.

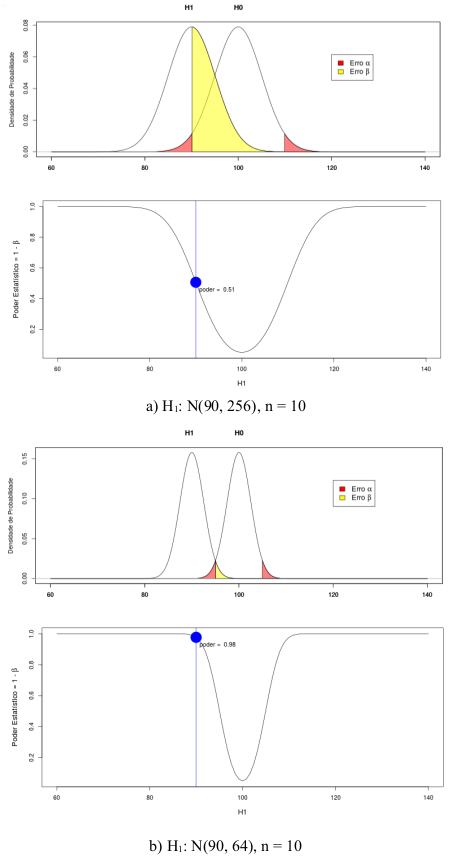
Figura 15.26: Aumento do poder estatístico com a redução do desvio padrão. A figura b corresponde a um desvio padrão igual à metade do desvio padrão da figura a.

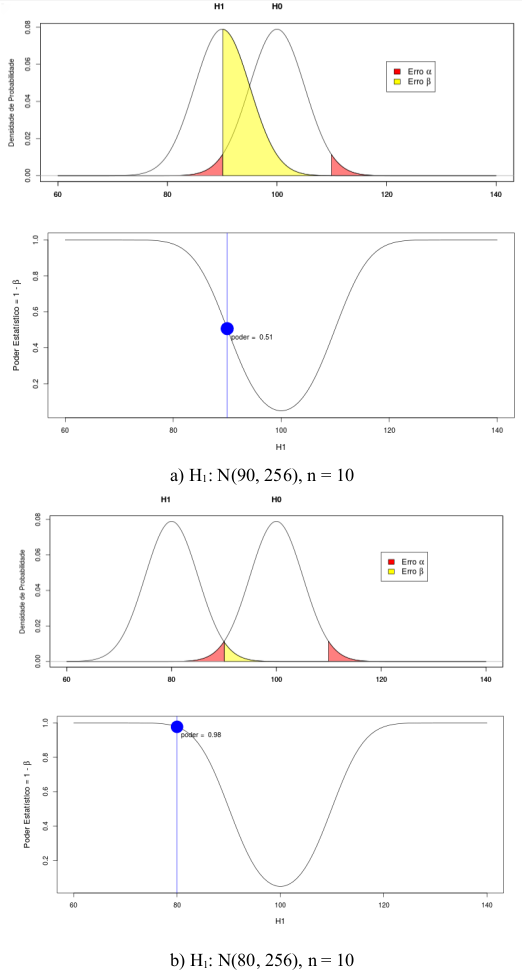
Figura 15.27: Aumento do poder estatístico com o aumento da distância entre a média de H₁ e a média de H₀. A figura b corresponde a uma distância igual ao dobro da distância na figura a.

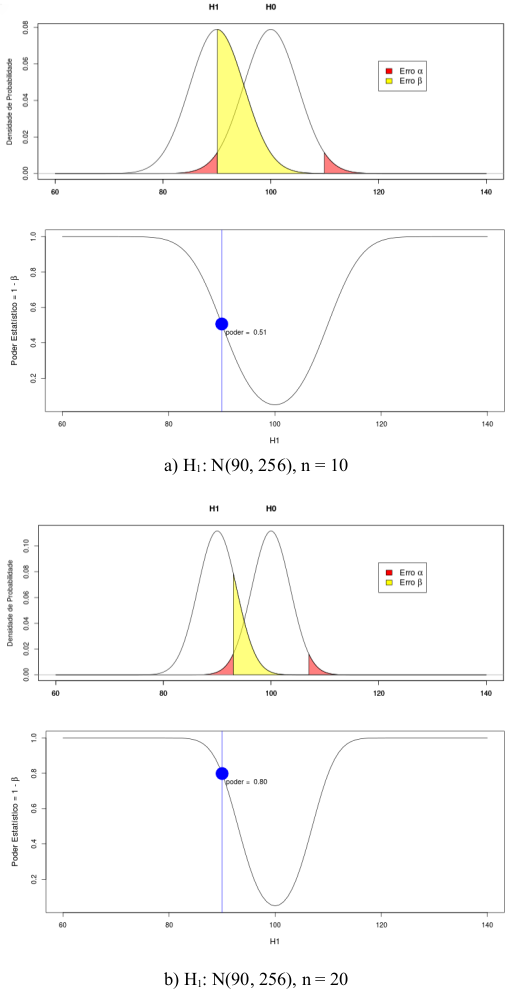
Figura 15.28: Aumento do poder estatístico com o aumento do tamanho amostral A figura b corresponde a um tamanho amostral igual ao dobro da amostra na figura a.

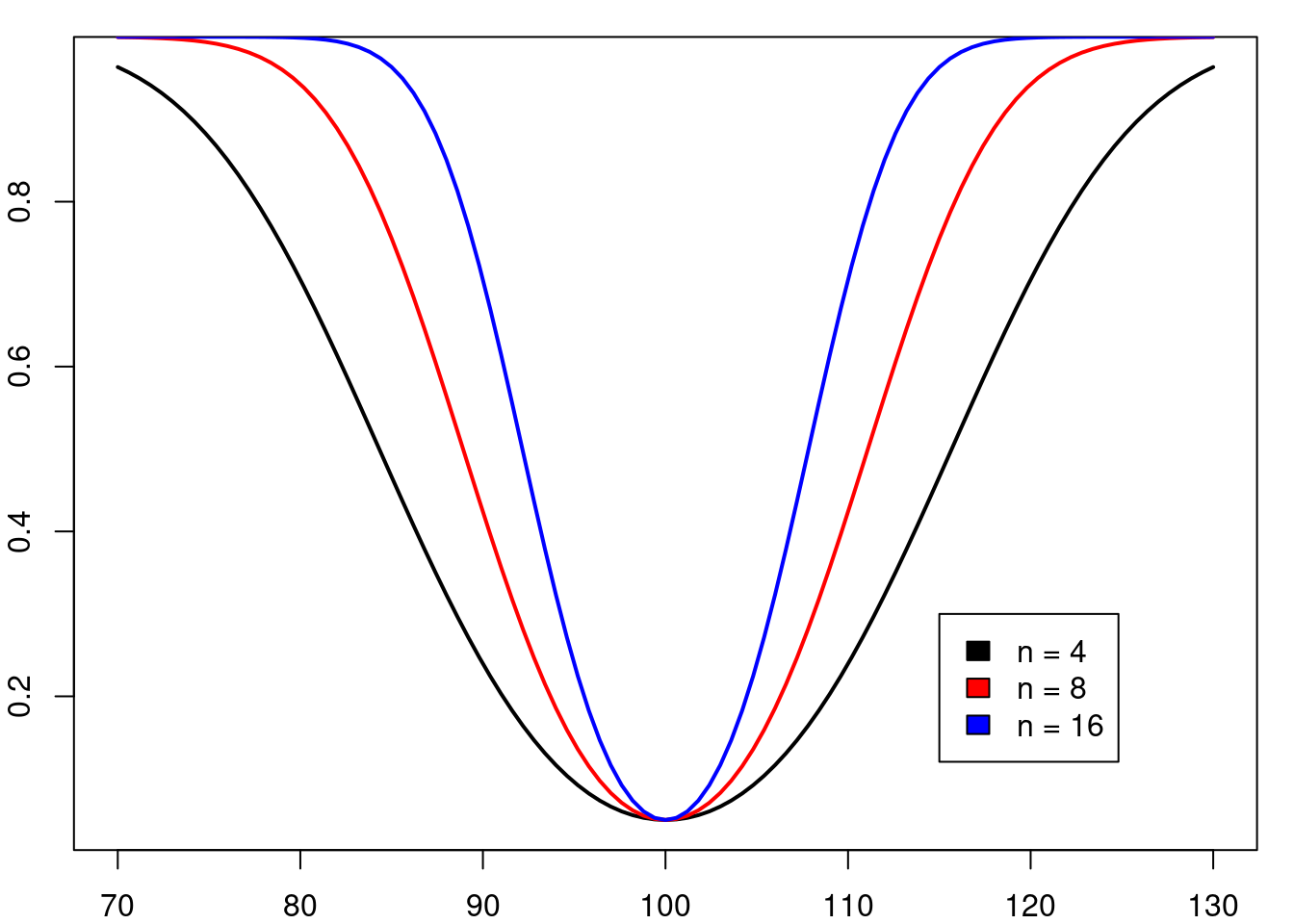
Figura 15.29: Função potência (poder estatístico) para diferentes valores do tamanho da amostra. O poder estatístico aumenta com o tamanho amostral.

15.11.1 Cálculo do tamanho amostral

Vamos ilustrar o cálculo do tamanho amostral para a situação onde a hipótese nula é que a amostra venha de uma população normal com média \(\mu_0\) e desvio padrão conhecido \(\sigma\).

hipótese nula ~ N(\(\mu_0\), \(\sigma^2\))

Vamos supor que, se a média real da população de onde extraímos a amostra seja \(\mu_1\), então desejamos que a amostra seja tal que tenhamos um poder estatístico 1 – \(\beta\) de rejeitar a hipótese nula. Vamos fixar o nível de significância para um teste bilateral igual a \(\alpha\). A figura 15.30 mostra a distribuição normal para a hipótese nula e para uma hipótese alternativa com média \(\mu_1\), as áreas correspondentes aos erros alfa e beta, e o valor crítico x_c.

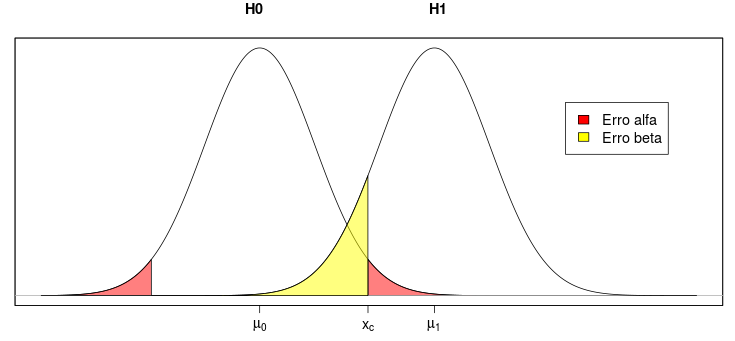
Figura 15.30: Figura auxiliar para o cálculo do tamanho amostral, uma vez fixado o poder estatístico e o erro tipo I.

A equação abaixo expressa o valor do quantil \(1-\alpha/2\) da distribuição normal padrão (\(z_{1-\alpha/2}\)), correspondente à área vermelha à direita na figura 15.30, em função de x_c, \(\mu_0\), \(\sigma\) e do tamanho amostral (n):

\[\begin{align} z_{1-\alpha/2} =\frac{x_c - \mu_0}{\frac{\sigma}{\sqrt{n}}} \tag{15.4} \end{align}\]

A equação abaixo expressa o valor do quantil \(\beta\) da distribuição normal padrão (\(z_{\beta}\)), correspondente à área amarela à esquerda na figura 15.30, em função de x_c, \(\mu_1\), \(\sigma\) e do tamanho amostral (n):

\[\begin{align} z_{\beta} =\frac{x_c - \mu_1}{\frac{\sigma}{\sqrt{n}}} \tag{15.5} \end{align}\]

Isolando x_c nas expressões (15.4) e (15.5), obtemos:

\[\begin{align} x_c = z_{1-\alpha/2}{\frac{\sigma}{\sqrt{n}}}+ \mu_0 \tag{15.6} \end{align}\]

\[\begin{align} x_c = z_{\beta}{\frac{\sigma}{\sqrt{n}}}+ \mu_1 \tag{15.7} \end{align}\]

Igualando (15.6) e (15.7), temos

\(\begin{aligned} &\ z_{1-\alpha/2}{\frac{\sigma}{\sqrt{n}}}+ \mu_0 = z_{\beta}{\frac{\sigma}{\sqrt{n}}}+ \mu_1\ \Rightarrow\ (z_{1-\alpha/2}- z_{\beta}){\frac{\sigma}{\sqrt{n}}}= \mu_1 - \mu_0 \end{aligned}\)

Logo:

\[\begin{align} n=\left[(z_{1-\alpha/2}- z_{\beta})\frac{\sigma}{\mu_1 - \mu_0}\right]^2 \tag{15.8} \end{align}\]

Confirmando o que foi mostrado na seção anterior, o tamanho amostral aumenta proporcionalmente ao quadrado do desvio padrão, ao inverso do quadrado da diferença entre os valores das médias para as duas hipóteses avaliadas e aumenta à medida que o erro beta e/ou alfa diminuem.

Exemplo: vamos considerar o problema do início do capítulo onde \(\mu_0\) = 85 mg/dl, \(\sigma\) = 16 mg/dl. Supondo que \(\alpha\) = 5%, vamos estimar o valor de n tal que tenhamos um erro \(\beta\) = 20%, se a média real da população for \(\mu_1\) = 92 mg/dl.

Portanto: \(z_{1-\alpha/2}\) = 1,96 e \(z_{\beta}\) = -0.84

Substituindo os valores em (15.8), obtemos:

\(\begin{aligned} n=\left[(1,96- (-0,84))\frac{16}{92-85}\right]^2 \Rightarrow\ n = 40,96 \Rightarrow\ n = 41 \end{aligned}\)

15.12 Teste de hipótese para pequenas amostras

Nesta seção, vamos realizar um teste de hipótese para a proporção de ocorrência de um evento que segue a distribuição binomial, porém sem poder recorrer a uma aproximação pela distribuição normal, pelo fato de que o tamanho amostral é pequeno. Nesse caso, temos que recorrer à distribuição exata do parâmetro de interesse.

Vamos considerar então uma população hipotética, de pessoas que sofrem de uma certa doença e que existe um tratamento padrão para essa doença com efetividade de 40%, ou seja 40% das pessoas que sofrem da doença e se submetem ao tratamento são curadas. Dessa forma, consideramos que a probabilidade de extrairmos uma pessoa ao acaso da população de doentes, submetê-la ao tratamento padrão e ela ficar curada é 40%.

Suponhamos agora que temos um tratamento experimental que acreditamos ser mais efetivo que o convencional. Vamos testar esse tratamento em uma amostra aleatória de 20 pessoas da população de doentes. Vamos supor também que as características da população não mudaram, que os pacientes não conseguem distinguir o tratamento novo do convencional e que os critérios para determinar a cura da doença são objetivos, de modo que a avaliação do estado do paciente após o tratamento não seja influenciada pelo tratamento recebido. Suponhamos que, dos 20 pacientes submetidos ao tratamento, 13 foram curados. Que conclusão devemos tirar?

Podemos realizar um teste de hipótese nesse cenário. Vamos seguir os passos típicos de um teste de hipótese.

PASSO 1: expressar o tema da pesquisa em termos de hipóteses estatísticas

Nesse exemplo, vamos considerar como hipótese nula a de que o tratamento novo não é melhor do que o convencional. A hipótese alternativa é que o tratamento novo é mais efetivo do que o convencional. Em termos estatísticos, podemos dizer que, para a hipótese nula, a proporção de pessoas curadas com o tratamento novo (p) é menor ou igual a 0,4. A hipótese alternativa é que essa proporção é acima de 0,4. Assim temos:

Hipótese Nula (H₀): p \(\le\) 0,4

Hipótese Alternativa (H1): p > 0,4

Nesse caso, o teste de hipótese será unilateral.

PASSO 2: decidir sobre um teste estatístico apropriado para testar a hipótese nula

Para testar a hipótese nula, vamos utilizar o número de curas observadas no estudo (13). De acordo com a hipótese nula, a variável número de curas em uma amostra de 20 pessoas segue uma distribuição binomial, X ~ Binomial (0,4; 20). Assim a estatística será o número de curas que observamos quando aplicamos o tratamento novo a uma amostra de 20 pessoas.

Vamos chamar de X a variável número de curas em uma amostra de 20 pessoas extraídas ao acaso da população de doentes e p a probabilidade de uma pessoa ficar curada após o tratamento padrão. A probabilidade de observarmos r curas na amostra de n = 20 é dada pela tabela 15.2. O gráfico dessa distribuição é mostrado na figura 15.31.

Tabela 15.2: Probabilidades associadas à observação de r curas (r = 0, 1, …, 20) em uma amostra de 20 pessoas, supondo a probabilidade de uma cura igual a 0,4.

X	P(X)
0	0.00003656
1	0.00048749
2	0.00308742
3	0.01234969
4	0.03499079
5	0.07464702
6	0.12441170
7	0.16588227
8	0.17970579
9	0.15973848
10	0.11714155
11	0.07099488
12	0.03549744
13	0.01456305
14	0.00485435
15	0.00129449
16	0.00026969
17	0.00004230
18	0.00000470
19	0.00000033
20	0.00000001

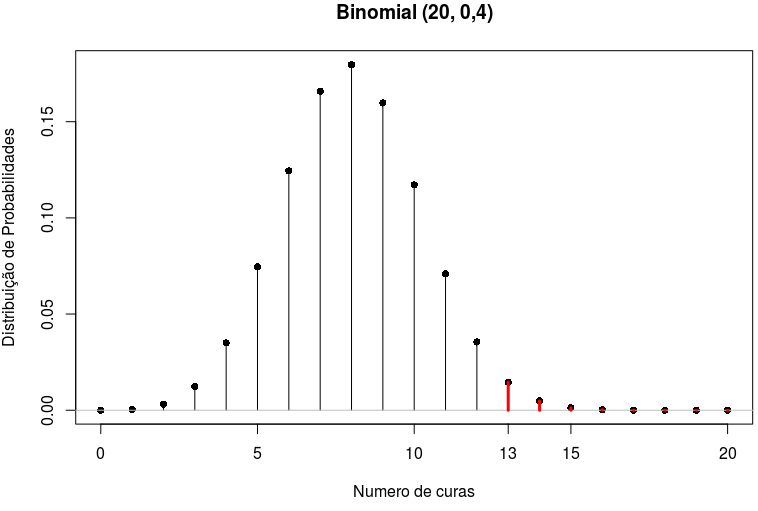
Figura 15.31: Distribuição de probabilidades para o número de curas em uma amostra de 20 pessoas, com p = 0,4. Em vermelho são as probabilidade de observarmos 13 ou mais curas em uma amostra aleatória de 20 pessoas.

PASSO 3: selecionar o nível de significância \(\alpha\)

Nesse exemplo, vamos selecionar \(\alpha\) = 5%.

PASSOS 4 e 5: Realizar os cálculos e tomar a decisão

Nesse caso, o valor de p será a probabilidade de observarmos um número de curas igual ou maior que 13 se a hipótese nula é verdadeira. Esse valor será a soma das probabilidades da tabela II para os valores de X no intervalo de 13 a 20, ou seja:

p = P(X=13)+P(X=14)+P(X=15)+P(X=16)+P(X=17)+P(X=18)+P(X=19)+P(X=20)

p = 0,0146+0,0049+0,0013+0,00027+0,000042+0,0000047+0,00000033+0,000000011

p = 0,021 = 2,1%

p < \(\alpha\)

Assim nós rejeitamos a hipótese nula e concluímos que o tratamento novo é mais efetivo que o convencional.

Como calcularíamos o valor de p se o teste acima fosse bilateral? Se antes de realizarmos o estudo, tivéssemos a suspeita de que o tratamento novo poderia também ser inferior ao convencional, nós realizaríamos um teste bilateral. Nesse caso, a hipótese nula seria que a efetividade do tratamento novo é igual à do tratamento convencional e a hipótese alternativa seria de que a efetividade do tratamento novo fosse diferente do tratamento convencional, ou seja:

Hipótese Nula (H₀): p = 0,4

Hipótese Alternativa (H1): p \(\neq\) 0,4

Como seria o teste de hipótese nesse caso?

O passo 1 seria alterado, sendo a hipótese nula e a hipótese alternativa como mostradas acima. O passo 2 e o passo 3 continuariam inalterados.

No passo 4, o cálculo do valor de p seria alterado. Ainda não existe um consenso sobre a forma de calculá-lo. Uma possível proposta é considerar como resultados extremos todos aqueles cuja probabilidade seja igual ou inferior à probabilidade do valor observado (definição 1). No exemplo, o valor de p para o teste bilateral seria então a soma de todas as probabilidades iguais ou inferiores a 0,0146, que é a probabilidade de observarmos 13 curas, supondo que a hipótese nula seja verdadeira.

Desse modo, o valor de p seria igual à soma:

p = P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=13)+P(X=14)+P(X=15)+P(X=16)+
      P(X=17)+P(X=18)+P(X=19)+P(X=20)

p = 0,000037 + 0,000487 + 0,0031 + 0,012 + 0,0146 + 0,0049 + 0,0013 + 0,00027 + 0,000042
    + 0,0000047 + 0,00000033 + 0,000000011 = 0,0367

ou seja p = 3,67%

Uma outra definição (definição 2), é a que utilizamos na seção 15.8, que parte das seguintes definições:

Valor p unilateral superior: é a probabilidade de se observar um valor igual ou acima do valor obtido no estudo, considerando a hipótese nula verdadeira.

Valor p unilateral inferior: é a probabilidade de se observar um valor igual ou abaixo do valor obtido no estudo, considerando a hipótese nula verdadeira.

O valor de p para um teste bilateral é definido como o dobro do menor dos dois valores p unilaterais. Por essa definição, o valor de p seria 2 x 2,1% = 4,2%

Existem outras definições do valor de p para testes bilaterais que não serão aqui abordadas.

Nesse exemplo, a conclusão continua inalterada, uma vez que p < \(\alpha\) para as duas definições de valor de p mostradas acima.

15.13 Interpretações incorretas do valor p

É importante chamar a atenção para algumas interpretações incorretas do valor p e mostrar por que elas estão equivocadas.

Interpretação errada 1: o valor p é a probabilidade de a hipótese nula ser verdadeira.

O valor p é justamente calculado com a suposição de que a hipótese nula seja verdadeira e a probabilidade expressa por p indica a compatibilidade entre a estatística observada na análise e a distribuição de probabilidades expressa pela hipótese nula.

Interpretação nem sempre correta 2: o valor p bilateral é a probabilidade de se observar um valor tão ou mais extremo que o obtido na amostra se a hipótese nula for verdadeira.

Essa interpretação é correta para o valor p em testes unilaterais. Em testes bilaterais, nem sempre ela produz valores corretos de acordo com as definições de valores p bilaterais apresentadas aqui, apesar de muitos livros textos fazerem essa interpretação. Vamos tomar um exemplo para mostrar por que essa interpretação não gera os mesmos valores de p que as duas definições de valor p bilateral dadas na seção anterior. Esse exemplo é extraído de Rothman e Greenland ((Rothman, Greenland, and Lash 2011), página 225). Suponhamos que uma enquete com 1000 pessoas tenha sido realizada para verificar a prevalência de HIV, e os investigadores estão testando a hipótese de que a prevalência de HIV naquela população seja de 0,005 (0,5%), utilizando um teste bilateral e a distribuição binomial. Nessa amostra de 1000 pessoas, 1 pessoa foi identificada com o vírus. Vamos calcular o valor p bilateral, segundo a interpretação acima.

Precisamos em primeiro lugar identificar o que seria um valor tão ou mais extremo que o obtido na amostra. A proporção de ocorrência do evento (pessoa com HIV) sob a hipótese nula é 0,005. Na amostra estudada, ocorreu 1 evento em 1000, logo a proporção de ocorrência do evento na amostra foi de 1/1000 = 0,001. A diferença entre essa proporção e a proporção sob a hipótese nula é: 0,005 – 0,001 = 0,004. Assim valores tão ou mais extremos na amostra seriam aqueles cujas proporções fossem abaixo de ou iguais a 0,001 ou acima de ou iguais a 0,005 + 0,004 = 0,009. Uma proporção igual a 0,009 corresponde a 9 pessoas com HIV em 1000. Assim, para obtermos o valor de p bilateral com essa interpretação, somaríamos as probabilidades de ocorrência de 9 ou mais pessoas com HIV, ou 1 ou menos pessoas com HIV, supondo que a prevalência fosse 0,005. Então o valor p bilateral seria:

      p = P[X \(\le\) 1] + P[X \(\ge\) 9]

Usando o R, o valor de P[X \(\le\) 1] é dado por:

pbinom(1, 1000, .005, lower.tail=TRUE)

## [1] 0.040091

O valor de P[X \(\ge\) 9] é dado por:

pbinom(8, 1000, .005, lower.tail=FALSE)

## [1] 0.06760297

Assim p = 0,04 + 0,067 = 0,11

Ao final da seção anterior, utilizamos duas definições do valor p bilateral frequentemente utilizadas:

definição 1: soma das probabilidades de todos os valores cuja probabilidade seja igual ou inferior à probabilidade do valor observado.

A probabilidade do valor observado (1) é igual a:

dbinom(1, 1000, .005)

## [1] 0.03343703

Observamos que as probabilidades de ocorrerem 9 ou 10 pessoas com HIV sob a hipótese nula são:

dbinom(9:10, 1000, .005)

## [1] 0.03613774 0.01799623

Assim os valores cujas probabilidades sejam menores do que 0,033 são 0, 1, e 10 em diante. Portanto, por essa definição, o valor de p seria igual a P[X \(\le\) 1] + P[X \(\ge\) 10]

pbinom(1, 1000, .005, lower.tail=TRUE) + pbinom(9, 1000, .005, 
                                                lower.tail=FALSE)

## [1] 0.07155624

definição 2: o dobro do menor valor entre o p unilateral superior e o p unilateral inferior.

Nesse caso, o valor de p seria o dobro de P[X \(\le\) 1]

p = 2 x 0,04 = 0,08

Vemos, portanto, que os valores de p para as duas definições dadas não coincidem com o valor de p obtido usando uma interpretação comumente utilizada. Devemos levar em conta, porém, que em distribuições de probabilidades simétricas, a interpretação de p bilateral apresentada aqui geraria o mesmo valor de p do que os obtidos pelas definições 1 e 2 acima. Mesmo em distribuições assimétricas, como o exemplo da seção anterior, a interpretação de p bilateral apresentada aqui geraria o mesmo valor de p do que a definição 1.

Interpretação errada 3: O valor de p é a probabilidade de ocorrência da estatística calculada a partir da amostra sob a hipótese nula.

Essa interpretação é totalmente incorreta. O valor de p unilateral inclui não somente a probabilidade da estatística calculada a partir da amostra sob a hipótese nula, como também as probabilidades sob a hipótese nula de todas as possíveis configurações de dados em que a estatística de teste seja mais extrema que a observada, para cima ou para baixo, dependendo do tipo de teste unilateral. No caso do valor de p bilateral, vide a discussão para a interpretação errada 2 acima.

Interpretação errada 4: Associar o valor p à significância clínica de um resultado. Vide seção 6.10.

15.14 Exercícios

1. Um ensaio controlado de um novo tratamento com o placebo levou ao resultado que o tratamento reduz o desfecho adverso estudado em relação ao placebo (p < 0,05, unilateral). Qual das afirmações abaixo você prefere? Comente.

   1. Foi provado que o tratamento é melhor que o placebo.
   2. Se o tratamento não é efetivo, há menos que 5% de probabilidade de se observar em uma amostra uma redução no valor do desfecho clínico menor ou igual à observada no estudo.
   3. O efeito observado do tratamento é tão grande que há menos que 5% de probabilidade que o tratamento não é melhor que o placebo.

2. O que significa o valor p em um teste de hipótese unilateral? E no bilateral?

3. Indique se cada afirmação abaixo é verdadeira ou falsa e justifique a resposta.

   1. O valor de p é a probabilidade de se obter um valor improvável.
   2. O valor de p está relacionado à qualidade do estudo.
   3. O valor de p abaixo do nível de significância indica que o estudo é importante clinicamente.
   4. Em geral, quanto maior o tamanho amostral, maior é o poder estatístico de um teste.
   5. O erro tipo II nunca pode ser menor que o erro tipo I.
   6. O erro tipo II é igual ao poder estatístico de um teste.
   7. O valor de p significa a probabilidade de se obter o valor da estatística avaliada na amostra, supondo que a hipótese nula é verdadeira.
   8. O erro tipo II está relacionado a uma hipótese alternativa, portanto seu valor depende com que hipótese alternativa você está trabalhando.
   9. O erro tipo I independe da hipótese alternativa.
   10. O intervalo de confiança é mais informativo do que o valor de p.

4. Suponhamos que você tenha “chutado” todos os itens da questão anterior e você está interessado em estimar as probabilidades de acertar um certo número de questões. Que distribuição de probabilidades você usaria? Qual a probabilidade de acertar 5 questões? E de acertar menos de 2?

5. Quais são os passos para se realizar um teste de hipótese?

6. As idades de uma amostra aleatória de 50 membros de uma certa população são obtidas e encontra-se que \(\bar{x} = 53,8\) anos e \(s = 9,89\) anos. A idade dessa população segue uma distribuição normal, mas não conhecemos nem a média nem a variância.

   1. Explique como você utilizaria os dados do enunciado para realizar um teste de hipótese bilateral de que a média de idade da população de membros da população é 52 anos.
   2. Em face da decisão tomada, que tipo de erro você pode ter cometido?
   3. Como você obteria o valor de p do teste e o que ele significa?

7. O que é nível de significância? Quais são os valores frequentemente usados?

8. Qual é o outro nome para o erro tipo II? O que é poder estatístico? Como encontrar o erro tipo II?

9. Que fatores influenciam o poder de um teste estatístico?

10. Por que intervalos de confiança são mais informativos do que testes de hipótese?

11. Um estudo controlado randomizado comparou o levamisol com o placebo para o tratamento de aftas. Os autores apresentaram a tabela exibida na figura 15.32, a qual realiza um teste estatístico (Mann-Whitney) para comparar os dois grupos de pacientes antes do tratamento. Por que isso não faz sentido?

Figura 15.32: Exemplo de uma situação onde um teste de hipótese não faz sentido. Fonte: quadro 1 do estudo intitulado “Levamisol não previne lesões de estomatite aftosa recorrente: um ensaio controlado randomizado, duplo-cego e controlado por placebo” (Weckx et al. 2009) (CC BY).

Referências

Rothman, Kenneth J, Sander Greenland, and Timothy L Lash. 2011. Epidemiologia Moderna. 3rd ed. Porto Alegre: Artmed.

Weckx, Luc Louis Maurice, Cleonice Hitomi Watashi Hirata, Marilda Aparecida Milanez Morgado Abreu, Vilma Ciorla Fillizolla, and Olga Maria Panhoca Silva. 2009. “Levamisol Não Previne Lesões de Estomatite Aftosa Recorrente: Um Ensaio Controlado Randomizado, Duplo-Cego e Controlado Por Placebo.” Revista Da Associação Médica Brasileira 55 (2): 132–38.