9 Variáveis aleatórias
9.1 Noção geral de variável aleatória
O conteúdo desta seção pode ser visualizado neste vídeo.
Iremos iniciar este capítulo apresentando uma conceituação formal para variável aleatória, tomando como exemplo uma máquina de caça-níquel simples. Esse exemplo foi adaptado do capítulo 5 do livro “Head First Statistics” (Griffiths 2008). Considerem a figura 9.1. A cada jogada, três figuras aparecem aleatoriamente na tela da máquina.

Figura 9.1: Máquina de caça-níquel. As três figuras à esquerda são os resultados que interessam e que podem dar algum ganho ao jogador. Os demais resultados resultam em perda para o jogador.
Suponhamos que a probabilidade de cada figura aparecer seja dada pela tabela 9.1.
| Figura | Probabilidade |
|---|---|
| Sete | 0,1 |
| Sino | 0,2 |
| Cereja | 0,2 |
| Outra figura | 0,5 |
Consideremos que o resultado de cada janela da máquina é independente dos resultados das demais janelas. O custo de cada jogada é R$ 5,00. Para cada configuração de resultados mostrada na figura 9.2, o jogador ganha algum dinheiro. O jogador não ganha nada se ocorrer qualquer outra configuração que não seja uma das mostradas na figura 9.2. Observem que o jogador ganha R$ 75,00 se ocorrerem dois setes e uma cereja em qualquer ordem, ou seja, dois setes seguidos de uma cereja, ou se ocorrer uma cereja entre dois setes, ou se ocorrer uma cereja seguida de dois setes.
Podemos conceber esse problema como um experimento, cujo espaço amostral S são as seguintes configurações:
S = {3 setes, 3 cerejas, 3 sinos, 2 setes/cereja em qualquer ordem, outras configurações}

Figura 9.2: Ganhos do jogador com cada uma das quatro configurações acima da máquina caça-níquel. O jogador não ganha nada com qualquer outro resultado. O jogador ganha R$ 75,00 com qualquer uma das configurações de uma cereja com dois setes.
O jogador está interessado em saber quais são as probabilidades de ocorrer cada uma das configurações mostradas na figura 9.2. Supondo que a probabilidade de cada figura aparecer é independente das demais, e utilizando os dados da tabela 9.1, podemos calcular facilmente as probabilidades de cada configuração:
P[3 setes] = P[sete] x P[sete] x P[sete] = 0,1 x 0,1 x 0,1 = 0,001
P[3 sinos] = P[sino] x P[sino] x P[sino] = 0,2 x 0,2 x 0,2 = 0,008
P[3 cerejas] = P[cereja] x P[cereja] x P[cereja] = 0,2 x 0,2 x 0,2 = 0,008
P[cereja, 2 setes] = P[cereja] x P[sete] x P[sete] + P[sete] x P[cereja] x P[sete]
+ P[sete] x P[sete] x P[cereja]
= 0,2 x 0,1 x 0,1 + 0,1 x 0,2 x 0,1 + 0,1 x 0,1 x 0,2
= 0,002 + 0,002 + 0,002
= 0,006
P[outra configuração] = 1 – ( P[3 setes] + P[3 sinos] + P[3 cerejas] + P[cereja, 2 setes])
= 1 – 0,001 – 0,008 – 0,008 – 0,006
= 0,977
A tabela 9.2 mostra as probabilidades de ocorrência de cada configuração do espaço amostral. Por isso tabelas desse tipo são chamadas Distribuições de Probabilidades, porque mostram como as probabilidades se distribuem para o conjunto de eventos disjuntos e exaustivos do espaço amostral.
| Configuração | Probabilidade |
|---|---|
| 3 Setes | 0,001 |
| 3 Sinos | 0,008 |
| 3 Cerejas | 0,008 |
| 2 Setes/1 Cereja | 0,006 |
| Outras | 0,977 |
A partir da distribuição de probabilidades da tabela 9.2, podemos calcular então as probabilidades dos possíveis lucros do jogador em cada jogada. Considerando que o jogador deve pagar R$ 5,00 para cada jogada, os possíveis lucros do jogador são:
3 Setes: R$ 100,00 – R$ 5,00 = R$ 95,00
3 Sinos: R$ 25,00 – R$ 5,00 = R$ 20,00
3 Cerejas: R$ 50,00 – R$ 5,00 = R$ 45,00
Setes/Cereja: R$ 75,00 – R$ 5,00 = R$ 70,00
Outra configuração: R$ 0,00 – R$ 5,00 = – R$ 5,00
Assim, a partir do espaço amostral de configurações possíveis da máquina de caça-níquel, podemos fazer um mapeamento para valores que são os lucros do jogador em cada configuração (figura 9.3). Vamos chamar esse mapeamento de variável X.
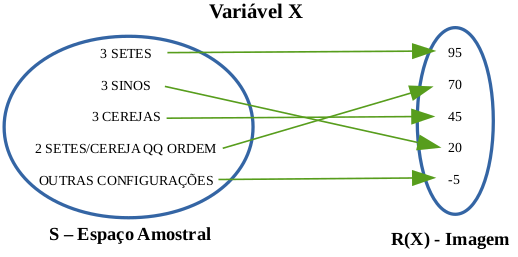
Figura 9.3: Mapeamento do espaço amostral da máquina de caça-níquel para a variável X.
Podemos associar a cada valor da imagem desse mapeamento a sua probabilidade de ocorrência (tabela 9.3). Essa tabela é a distribuição de probabilidades da variável X. Pelo fato dessa variável possuir uma distribuição de probabilidades, ela é chamada de Variável Aleatória.
| Lucro | Probabilidade |
|---|---|
| 95 | 0,001 |
| 20 | 0,008 |
| 45 | 0,008 |
| 70 | 0,006 |
| -5 | 0,977 |
Todo esse raciocínio motiva a seguinte
Definição: Sejam um experimento e S um espaço amostral associado ao experimento. Uma função X, que associa a cada elemento \(s \in S\) um número real X(s), é denominada variável aleatória.
Uma variável aleatória corresponde a um resultado numérico de um experimento e é usualmente representada por letras maiúsculas, como X, Y, Z, T, W. Os valores observados de uma variável aleatória X usualmente são representados por letras minúsculas, xi , i = 1, 2, … N, onde N representa o número de experimentos.
Portanto uma variável aleatória é uma variável que está associada a uma distribuição de probabilidades.
Seja X uma variável aleatória. Se o conjunto de valores possíveis de X for finito ou infinito enumerável, chamamos X de variável aleatória discreta, isto é, os valores possíveis de X podem ser dispostos em ordem crescente e serem associados cada um a um número inteiro positivo em ordem crescente.
9.2 Valor esperado de uma variável aleatória discreta
Os conteúdos desta seção e da seção 9.3 podem ser visualizados neste vídeo.
Um dos interesses do jogador é saber o quanto ele esperaria lucrar em cada jogada na máquina de caça-níquel. Vamos raciocinar da seguinte forma: se o jogador jogasse 1.000 vezes com a distribuição de probabilidades do lucro expressa na tabela 3, então ele esperaria 1 vez lucrar R$ 95,00 (0,001 x 1000), R$ 70,00 em 6 vezes, R$ 45,00 em 8 vezes, R$ 20,00 em 8 vezes e perderia R$ 5,00 em 977 vezes. Então o lucro esperado do jogador (L) em 1.000 jogadas seria:
L = 95 x 1 + 70 x 6 + 45 x 8 + 20 x 8 – 5 x 977
L = – R$ 3.850,00
ou seja, o jogador perderia R$ 3.850,00 em 1.000 jogadas. Assim, em média, ele perderia R$ 3,85 por jogada.
Usando a seguinte notação
x1 = 95, p1 = P[X = 95]
x2 = 70, p2 = P[X = 70]
x3 = 45, p3 = P[X = 45]
x4 = 20, p4 = P[X = 20]
x5 = -5, p5 = P[X = -5]
vamos denominar Ljogo como o valor esperado da variável X e usar a notação E[X].
Logo:
\[\begin{align} L_{jogo} = E[X] =95\frac{1}{1000}+70\frac{6}{1000}+45\frac{8}{1000}+20\frac{8}{1000}-5\frac{977}{1000} = -3,85 \tag{9.1} \end{align}\]
\(\begin{aligned} &\ E[X]=x_1.p_1+x_2.p_2+x_3.p_3+x_4.p_4+x_5.p_5 \\ \\ &\ E[X]=\sum_{i=1}^{5}x_i p_i \end{aligned}\)
O lucro esperado em cada jogada (Ljogo) pode ser calculado como a média ponderada dos ganhos possíveis, onde o peso é a probabilidade de ocorrência de cada ganho. Assim podemos adotar a seguinte definição de valor esperado para uma variável aleatória discreta qualquer:
Valor esperado: Seja X uma variável aleatória discreta e que tenha associada uma distribuição de probabilidade p(x), isto é, X pode assumir valores x1, x2, …, xN com probabilidades p1, p2, …, pN. O valor esperado de X, E[X], é definido por:
\[\begin{align} E[X]=\sum_{i=1}^{N}x_i p_i \tag{9.2} \end{align}\]
E[X] representa o valor esperado, ou esperança matemática, da variável aleatória X. Ao contrário da probabilidade, o valor esperado não se restringe ao intervalo [0,1]. Quando estamos tratando de variáveis aleatórias condicionadas, assim como no caso de probabilidade condicional, escrevemos E(X|F), ou seja, o valor esperado de X dado que o evento F ocorreu.
Em geral nos referimos ao valor esperado como sendo a média da variável aleatória e representamos E[X] simplesmente por \(\mu\).
Vamos simular a máquina caça-níqueis no R? Inicialmente, criamos dois vetores contendo os valores da variável x e as probabilidades de ocorrência de cada valor, respectivamente:
Em seguida vamos simular 1000 jogadas por meio da função sample:
Esse comando vai tomar 1000 amostras de x com repetição, onde cada valor de x tem a probabilidade definida por px. Em seguida, a função table irá indicar a frequência de cada valor de x na amostra. Um exemplo seria:
## lucro
## -5 20 45 70
## 972 6 14 8O lucro médio dessas 1000 jogadas é dado pela função mean aplicada à tabela de lucros:
## [1] -3.55Observem que o número de ocorrências dos diversos valores possíveis para o lucro em cada jogada são próximos, mas não necessariamente iguais ao número de ocorrências esperados e o lucro médio é próximo ao valor esperado calculado em (9.1) (R$ -3,85). Se simularmos novamente, os resultados serão ligeiramente diferentes:
## lucro
## -5 20 45 70 95
## 978 6 8 6 2## [1] -3.8Dá para notar que a probabilidade de ganhar no jogo é muito pequena, não é? Também é possível verificar que as frequências observadas são próximas das esperadas, assim como o lucro médio. Se aumentarmos o número de amostras, as frequências dos valores vão se aproximar ainda mais das frequências esperadas. Vamos simular mais uma vez, agora com 1.000.000 de jogadas.
## lucro
## -5 20 45 70 95
## 977125 7904 7978 5991 1002## [1] -3.8539759.3 Variância de uma variável aleatória discreta
Nem todas as jogadas de nossa máquina caça-níquel irão resultar no mesmo valor de ganho. Na grande maioria das vezes, iremos perder, mas eventualmente podemos ganhar alguma coisa. Assim poderemos estar interessados em uma medida de variabilidade dos nossos ganhos. Vimos no capítulo 3 que uma das medidas mais utilizadas para avaliar a dispersão dos dados é a variância, ou a sua raiz quadrada, que é o desvio padrão.
Também vimos que a variância de uma amostra de n elementos é calculada da seguinte forma:
\[s^2 = \frac{1}{n-1} \sum_{i=1}^{n}(x_{i}-\bar{x})^2\]
Quando se conhece o valor esperado da variável X (\(\mu\)), o cálculo da variância é realizado substituindo-se (n-1) na fórmula acima por n.
Se houver k valores diferentes na amostra e o valor xj (j=1, …, k) ocorrer nj vezes, multiplicamos (xj – \(\mu\))2 por nj, somamos os produtos nj (xj – \(\mu\))2, para todos os valores xj, e dividimos a soma por n. Fazendo pj = P[X=xj] e chamando a variância de X de var[X], temos:
\[\begin{align} var[X] = \frac{1}{n} \sum_{j}^{n}n_j(x_{j}-\mu)^2 = \sum_{j=1}^{k}\frac{n_j(x_{j}-\mu)^2}{n} = \sum_{j=1}^{k}{p_j(x_{j}-\mu)^2} \tag{9.3} \end{align}\]
Isso sugere a seguinte
Definição: Dada uma variável aleatória discreta X, com k valores distintos, a variância de X, denotada por \(\sigma^2\), é expressa por:
\[\begin{align} var[X]= \sigma^2 = \sum_{j=1}^{k}{p_j(x_{j}-\mu)^2}=E[(X-\mu)^2] \tag{9.4} \end{align}\]
O desvio padrão, denotado por \(\sigma\), é a raiz quadrada da variância:
\[\begin{align} \sigma[X]= \sqrt{var[X]} \tag{9.5} \end{align}\]
Vamos calcular a variância do ganho por jogada na nossa máquina de caça-níquel.
var[X] = (95-(-3,85))2 x 0,001 + (70-(-3,85))2 x 0,006 + (45-(-3,85))2 x 0,008
+ (20-(-3,85))2 x 0,008 + (-5-(-3,85))2 x 0,977
= 98,852 x 0,001 + 73,852 x 0,006 + 48,852 x 0,008 + 23,852 x 0,008
+ (-1,15)2 x 0,977
= 67,428
Portanto \(\sigma\)[X] = \(\sqrt{67,428}\) = 8,21
Vamos calcular a variância e o desvio padrão da amostra de 1.000.000 que obtivemos na seção anterior do R:
## [1] 67.29107## [1] 8.2031139.4 Transformação linear
O conteúdo desta seção pode ser visualizado neste vídeo.
Suponhamos que tenha sido realizada uma alteração na nossa máquina de caça-níquel. Agora, os valores dos prêmios foram multiplicados por 5 e cada jogada passou a custar R$ 10,00, sendo as probabilidades mantidas como eram antes. Assim a probabilidade de o jogador ganhar R$ 500,00 é 0,001; de ganhar R$ 375,00 é 0,006; e assim por diante. Qual seria o novo ganho esperado e a sua variância?
Vamos chamar de Y o lucro líquido do jogador nessa nova configuração da máquina caça-níquel. A tabela 9.4 mostra a distribuição de probabilidades de Y. Recordando como montar esta tabela, se numa jogada o jogador obtivesse 3 setes, então ele ganharia R$ 500,00 e gastaria R$ 10,00. Assim o ganho líquido dele seria R$ 490,00. De maneira análoga, obtemos as demais linhas da tabela 9.4.
| Lucro | Probabilidade |
|---|---|
| 490 | 0,001 |
| 115 | 0,008 |
| 240 | 0,008 |
| 365 | 0,006 |
| -10 | 0,977 |
O valor esperado e a variância de Y poderiam ser calculados por meio das fórmulas apresentadas na seção anterior. Porém vamos calculá-los de outra maneira para ilustrar o conceito de transformação linear de uma variável aleatória.
Na introdução deste capítulo, foi visto que a variável X, o lucro em uma jogada com a máquina caça-níquel, podia ser expressa por:
\[\begin{align} X = G - 5 \tag{9.6} \end{align}\]
onde G é o ganho na jogada e 5 era o que o jogador pagava em cada jogada.
Na nova configuração da máquina caça-níquel, o lucro (variável Y) passa a ser:
\[\begin{align} Y = 5G - 10 \tag{9.7} \end{align}\]
onde G era o ganho na configuração anterior.
Substituindo G = X + 5 da expressão (9.6) em (9.7), obtemos:
Y = 5(X + 5) - 10
Logo: Y = 5X +15
Uma expressão desse tipo é chamada de transformação linear. Assim temos a seguinte definição:
Transformação Linear: dada uma variável aleatória X, e dois números reais \(a\) e \(b\), então a variável \(Y = aX + b\) é uma transformação linear da variável X.
Se conhecermos o valor esperado de X, o valor esperado de Y pode ser calculado da seguinte forma, supondo que X tenha N elementos distintos:
\(E[Y] =E[aX+b]\)
\(=\sum_{i=1}^{N}(ax_i+b) p_i\)
\(=\sum_{i=1}^{N}ax_i p_i+\sum_{i=1}^{N}b p_i\)
\(=a\sum_{i=1}^{N}x_i p_i+b\sum_{i=1}^{N}p_i\)
Logo:
\[\begin{align} \boldsymbol{E[Y] =aE[X]+b} \end{align}\]
Então, para o exemplo acima, como Y = 5X + 15, o valor esperado de Y será:
E[Y] = 5E[X] + 15 = 5 x (-3,85) + 15
E[Y] = -4,25
Se conhecermos a variância de X, a variância de Y pode ser calculada da seguinte forma:
\(var[Y] =var[aX+b]= E[(aX+b-E[aX+b])^2]\)
\(=E[(aX+b-aE[X]-b)])^2]\)
\(=E[(aX-a\mu)^2]\)
\(=E[(a(X-\mu)^2]\)
\(=E[a^2(X-\mu)^2]\)
\(=a^2E[(X-\mu)^2]\)
Logo:
\[\begin{align} \boldsymbol{var[Y] =a^2var[X]} \end{align}\]
Desse modo, numa transformação linear, a variância é multiplicada pelo quadrado da constante a. A constante b não influencia na dispersão da nova variável. Isso é razoável, já que se apenas somarmos uma constante a todos os valores de uma variável aleatória, então todos os seus valores terão o mesmo deslocamento, inclusive a sua média, e a dispersão em torno da nova média não irá ser alterada.
Para o exemplo acima, como Y = 5X + 15, a variância de Y será:
var[Y] = 52 var[X] = 25 x 67,428
var[Y] = 1685,70 → \(\sigma\)[Y] = 41,06
Vamos simular esta transformação no R? Lembramos novamente que os valores de variância e desvio padrão que você obtiver irão diferenciar dos obtidos a seguir, devido ao fato de que as suas amostras serão diferentes das obtidas neste exemplo.
## [1] 490 365 240 115 -10## [1] 1682.921## [1] 41.023429.5 Soma de variáveis aleatórias
O conteúdo desta seção pode ser visualizado neste vídeo.
Vamos supor agora que temos duas máquinas caça-níquel com as probabilidades de lucro definidas pela tabela 3. Vamos supor que o resultado de uma jogada em uma das máquinas independe do resultado de uma jogada na outra máquina. Um casal, Ana e Carlos, joga em cada uma das máquinas. Qual é a distribuição de probabilidades do lucro dos dois juntos? Quanto eles esperam lucrar juntos? Qual é a variância do lucro deles?
Vamos considerar X como o lucro obtido por Ana e Y o lucro obtido por Carlos em uma jogada. Então o lucro dos dois é a soma de X e Y. Vamos chamar essa soma de Z. Então:
Z = X + YQual é a distribuição de probabilidades de Z?
Em primeiro lugar, vamos verificar quais são os valores que Z pode assumir. Tanto X como Y podem assumir os valores 95, 70, 45, 20 e -5. Como X e Y são independentes, então Z pode assumir a soma de qualquer combinação dos valores de X e Y. Logo teríamos:
X = 95, Y = 95 → Z = 190
X = 95, Y = 70 → Z = 165
X = 95, Y = 45 → Z = 140
…………….
X = -5, Y = 20 → Z = 15
X = -5, Y = -5 → Z = -10
Como os pares (X, Y) (95, 70) e (70, 95) geram o mesmo valor de Z, assim como os pares (95, 45) e (45, 95), (95, 20) e (20, 95) etc., teríamos um total de 9 diferentes valores para Z (tabela 9.5).
Para calcularmos as probabilidades de ocorrência de cada valor de Z, vamos considerar inicialmente a probabilidade de Z = 190, ou seja, X = 95 e Y = 95:
P[Z=190] = P[X=95, Y=95]
Como as variáveis aleatórias X e Y são independentes, então
P[Z=190] = P[X=95] . P[Y=95] = 0,001 . 0,001 = 0,000001
Analogamente, teríamos:
P[Z=165] = P[X=95, Y=70] + P[X=70, Y=95] = 2 . 0,001 . 0,006 = 0,000012
e assim por diante. Calculando as probabilidades para cada valor de Z, obteremos a distribuição de probabilidades de Z, mostrada na tabela 9.5.
A partir da distribuição de Z, poderíamos calcular os valores de E[Z] e var[Z]. Porém vamos obtê-los de uma forma diferente, supondo que X e Y possam assumir, respectivamente, N1 e N2 elementos distintos (na tabela 9.5, N1 = N2 = 5). Temos:
\(E[Z]=E[X+Y] = \sum_{i=1}^{N1}\sum_{j=1}^{N2}(x_i+y_j)P[X= x_i, Y= y_j]\)
\(\ \ \ \ \ \ \ = \sum_{i=1}^{N1}\sum_{j=1}^{N2}x_iP[X= x_i, Y= y_j]+\sum_{i=1}^{N1}\sum_{j=1}^{N2}y_jP[X= x_i, Y= y_j]\)
\(\ \ \ \ \ \ \ =\sum_{i=1}^{N1}x_i\sum_{j=1}^{N2}P[X= x_i, Y= y_j]+\sum_{j=1}^{N2}y_j\sum_{i=1}^{N1}P[X= x_i, Y= y_j]\)
\(\ \ \ \ \ \ \ =\sum_{i=1}^{N1}x_iP[X= x_i]+\sum_{j=1}^{N2}y_jP[Y= y_j]\)
Logo:
\[\begin{align} \boldsymbol{E[Z] = E[X+Y] = E[X]+E[Y]} \end{align}\]
| X | Y | Z | P[Z] |
|---|---|---|---|
| 95 | 95 | 190 | 0,000001 |
| 95 | 70 | 165 | 0,000012 |
| 70 | 95 | ||
| 95 | 45 | 140 | 0,000052 |
| 45 | 95 | ||
| 70 | 70 | ||
| 95 | 20 | 115 | 0,000112 |
| 20 | 95 | ||
| 70 | 45 | ||
| 45 | 70 | ||
| 95 | -5 | 90 | 0,002114 |
| -5 | 95 | ||
| 45 | 45 | ||
| 70 | 20 | ||
| 20 | 70 | ||
| 70 | -5 | 65 | 0,011852 |
| -5 | 70 | ||
| 45 | 20 | ||
| 20 | 45 | ||
| 45 | -5 | 40 | 0,015696 |
| -5 | 45 | ||
| 20 | 20 | ||
| 20 | -5 | 15 | 0,015632 |
| -5 | 20 | ||
| -5 | -5 | -10 | 0,954529 |
Assim o valor esperado de uma variável aleatória que é a soma de duas outras variáveis aleatórias é a soma dos valores esperados de cada uma das variáveis que compõem as parcelas da soma. Observem que, na demonstração acima, nenhuma consideração foi realizada sobre a independência das variáveis X e Y. Essa propriedade não depende da hipótese de independência das variáveis.
Para obtermos uma expressão para a variância de Z, vamos tomar E[X] = \(\mu\)x , E[Y] = \(\mu\)y , e aplicar a fórmula para o cálculo da variância:
\(var[Z]=var[X+Y] = E[(X+Y-E[X+Y])^2]\)
\(\ \ \ \ \ \ \ \ \ =E[(X-E[X] + Y-E[Y])^2]\)
\(\ \ \ \ \ \ \ \ \ =E[(X-\mu_x + Y-\mu_y)^2]\)
\(\ \ \ \ \ \ \ \ \ =E[(X-\mu_x)^2 + (Y-\mu_y)^2 + 2(X-\mu_x)(Y-\mu_y)]\)
\(\ \ \ \ \ \ \ \ \ =E[(X-\mu_x)^2] + E[(Y-\mu_y)^2] + 2E[(X-\mu_x)(Y-\mu_y)]\)
\[\begin{align} \boldsymbol{var[Z] = var[X]+var[Y]+2E[(X-\mu_x)(Y-\mu_y)]} \tag{9.8} \end{align}\]
Assim a variância da soma de duas variáveis aleatórias é igual à soma das variâncias de cada uma das variáveis e um terceiro termo. Quando as variáveis são independentes, então o terceiro termo será igual a zero, como mostraremos a seguir.
9.6 Independência de variáveis aleatórias
Dadas duas variáveis aleatórias X e Y, independentes, temos como uma propriedade básica do valor esperado que E[XY] = E[X]E[Y]. Para demonstrarmos essa propriedade, recorremos à propriedade do valor esperado de uma função de uma variável aleatória, no caso a função f = XY:
\(E[XY] = \sum_{i=1}^{N1}\sum_{j=1}^{N2} (x_i y_j) P[X=x_i, Y=y_j]\)
\(\ \ \ \ \ \ \ \ \ \ \ = \sum_{i=1}^{N1}\sum_{j=1}^{N2} x_i y_j P[X=x_i]P[Y=y_j]\)
\(\ \ \ \ \ \ \ \ \ \ \ =\sum_{i=1}^{N1} x_i P[X=x_i]\sum_{j=1}^{N2} y_j P[Y=y_j]\)
\(=\sum_{i=1}^{N1} x_i P[X=x_i]\sum_{j=1}^{N2} y_j P[Y=y_j]\)
\(\boldsymbol{E[XY] =E[X]E[Y]}\)
Para variáveis aleatórias independentes, o valor esperado do produto de duas variáveis aleatórias é igual ao produto dos valores esperados de cada uma das variáveis. Se as variáveis não forem independentes, esse resultado não é válido.
O terceiro termo da expressão (9.8) pode ser desenvolvido e, assumindo X e Y independentes, resulta em:
\(E[(X-\mu_x)(Y-\mu_y)] = E[XY]- \mu_yE[X]-\mu_xE[Y]+E[\mu_x\mu_y]\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = E[X]E[Y]- \mu_x\mu_y-\mu_x\mu_y+\mu_x\mu_y\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \mu_x\mu_y-\mu_x\mu_y-\mu_x\mu_y+\mu_x\mu_y\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 0\)
Logo, para variáveis independentes, temos:
\(\boldsymbol{var[X+Y] = var[X] + var[Y]}\)
Para o exemplo da seção anterior, var[Z=X+Y] = 67,428 + 67,428 = 134,856
Caso a variável aleatória fosse Z = X – Y, X e Y independentes, podemos mostrar facilmente que:
\(\boldsymbol{E[Z] = E[X-Y] = E[X] - E[Y]}\)
\(\boldsymbol{var[Z] = var[X-Y] = var[X] + var[Y]}\)
Assim o valor esperado da diferença de duas variáveis aleatórias é a diferença dos valores esperados das duas variáveis e a variância da diferença, assim como a variância da soma, é a soma das variâncias, desde que as variáveis sejam independentes.
Generalizando um pouco mais, se X e Y são duas variáveis aleatórias, e
\(\boldsymbol{Z = aX + bY}\)
então:
\[\begin{align} \boldsymbol{E[Z] = aE[X] + bE[Y]} \end{align}\]
Além disso, se X e Y são variáveis aleatórias independentes, então:
\[\begin{align} \boldsymbol{var[X+Y] = a^2 var[X] + b^2 var[Y]} \end{align}\]
Os resultados acima podem ser estendidos para a soma de mais de duas variáveis, ou seja, o valor esperado da soma de duas ou mais variáveis será sempre a soma dos valores esperados das variáveis. Assumindo independência entre as variáveis aleatórias, a variância da soma de duas ou mais variáveis será sempre a soma das variâncias dessas variáveis.
Resumindo, se X e Y são variáveis aleatórias, então:
\(\boldsymbol{E[kX] = kE[X]}\)
\(\boldsymbol{E[aX \pm bY]= aE[X] \pm bE[Y]};\ a\ e\ b\) constantes
\(\boldsymbol{E[XY] = E[X]E[Y]}\), se X e Y são independentes
\(\boldsymbol{E[X-E[X]] = 0}\)
\(\boldsymbol{var[aX \pm bY]= a^2 var[X] + b^2var[Y]}\), se X e Y são independentes
\(\boldsymbol{var[cX] = c^2 var[X]}\)
Finalmente sejam X1, X2, X3, …, Xn n variáveis independentes, onde E[Xi] = \(\mu\) e var[Xi] = \(\sigma\)2, ou seja, n variáveis aleatórias com a mesma média e a mesma variância. Nesse caso, se Sn é a soma dessas variáveis aleatórias:
\(S_n = X_1 + X_2 + X_3 + \dots + X_n\)
e \(\bar{X}\) é a média das variáveis X1, X2, X3, …, Xn:
\(\bar{X} = \frac{\sum_{i=1}^{n}{ X_i}}{n}\),
teremos os seguintes resultados importantes:
\(\boldsymbol{E[S_n] = n\mu}\)
\(\boldsymbol{var[S_n] = n\sigma^2}\)
\(\boldsymbol{E[\bar{X}] = \mu}\)
\(\boldsymbol{var[\bar{X}] = \frac{\sigma^2}{n}}\)
9.7 Exercício
Um jogo consiste no lançamento de um dado não viciado. Se ocorrer 6, a pessoa ganha R$ 100,00. Se ocorrer qualquer outro resultado, ela perde R$ 25,00.
- Se a pessoa lançar o dado uma vez, qual é a distribuição de probabilidades do valor recebido pela pessoa? Qual é o valor esperado do seu ganho?
- Se duas pessoas jogam cada uma o dado, qual a distribuição de probabilidades do ganho das duas pessoas juntas? Qual é o valor esperado do ganho das duas pessoas juntas?
- Se o jogo se altera e os valores são triplicados para cada ocorrência do dado, qual é a distribuição de probabilidades do valor recebido pela pessoa? Qual é o valor esperado do seu ganho?